We can perform cross-validation using tune() to select the best choice of
gamma and cost for an SVM with a radial kernel:
set.seed(1)
tune.out = tune(svm, y ~ ., data = dat[train,], kernel = "radial", ranges = list(cost = c(0.1, 1, 10, 100, 1000), gamma = c(0.5, 1, 2, 3, 4)))
summary(tune.out)
Parameter tuning of ‘svm’:
- sampling method: 10-fold cross validation
- best parameters:
cost gamma
1 0.5
- best performance: 0.07
- Detailed performance results:
cost gamma error dispersion
1 1e-01 0.5 0.26 0.15776213
2 1e+00 0.5 0.07 0.08232726
3 1e+01 0.5 0.07 0.08232726
4 1e+02 0.5 0.14 0.15055453
5 1e+03 0.5 0.11 0.07378648
6 1e-01 1.0 0.22 0.16193277
7 1e+00 1.0 0.07 0.08232726
...
Therefore, the best choice of parameters involves cost=1 and gamma=0.5. We
can view the test set predictions for this model by applying the predict()
function to the data. Notice that to do this we subset the dataframe dat
using -train as an index set.
table(true = dat[-train, "y"], pred = predict(tune.out$best.model, newdata = dat[-train,]))
pred
true 1 2
1 67 10
2 2 21
12% of test observations are misclassified by this SVM.
Questions
Different kernels can solve different problems. In this case we will try to solve a classification problem where the data is divided into a outer and inner circle:
make.circle.data = function(n) {
x1 = runif(n, min = -1, max = 1)
x2 = x1
y1 = sqrt(1 - x1^2)
y2 = (-1)*y1
x1 = c(x1,x2)
x2 = c(y1,y2)
return(data.frame(x1, x2))
}
set.seed(2077)
df1 = make.circle.data(30)
df2 = make.circle.data(30)
df1 = df1 * .5 + rnorm(30, 0, 0.05)
df2 = df2 + rnorm(30, 0, 0.05)
df = rbind(df1, df2)
z = rep(c(-1, 1), each=60)
plot(df, col=z+3)
dat = data.frame(x=df, y = as.factor(z))
names(dat) = c('x.1', 'x.2', 'y')
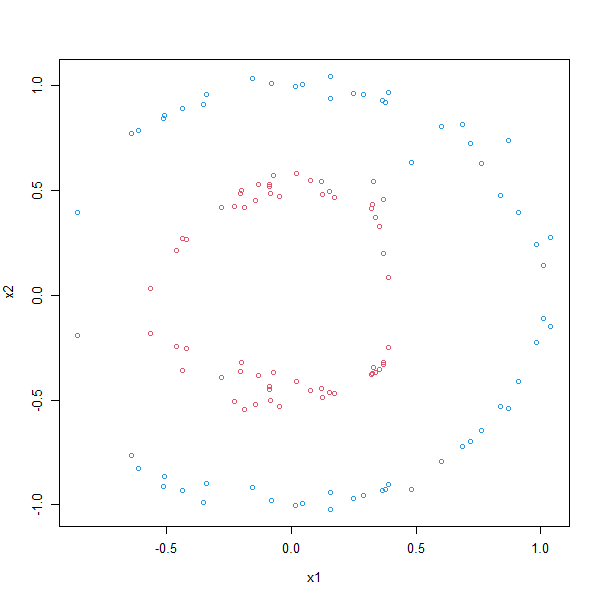
- Split the dataframe dat into a train-validate set and a test set with a 80-20 split.
Use the
sample()function to randomly sample the data. Store the train-validate data intrainand test data intest. - Build three models each with a different kernel: linear, polynomial and radial. For each model:
- Tune the model by performing ten-fold cross-validation and finding the best parameter value for
costin the range (0.01, 0.1, 1, 10, 100).- For the polynomial also find the best parameter value of
degreein the range (2, 3, 4, 5). - For the radial also find the best parameter value of
gammain the range (0.5, 1, 2, 3, 4). Store the outcomes inlin.tune.out,poly.tune.outandrad.tune.outrespectively
- For the polynomial also find the best parameter value of
- Predict the classes for the test data using the best model gotten from cross-validation.
Store the predictions in
lin.pred,poly.predandrad.predrespectively.
- Tune the model by performing ten-fold cross-validation and finding the best parameter value for
- For each model look at the
plot(BEST_MODEL, test)and answer the next multiple choice question
MC1: Which kernel is best able to solve the classification problem?
1) linear
2) polynomial
3) radial
Assume that:
- The
e1071library has been loaded