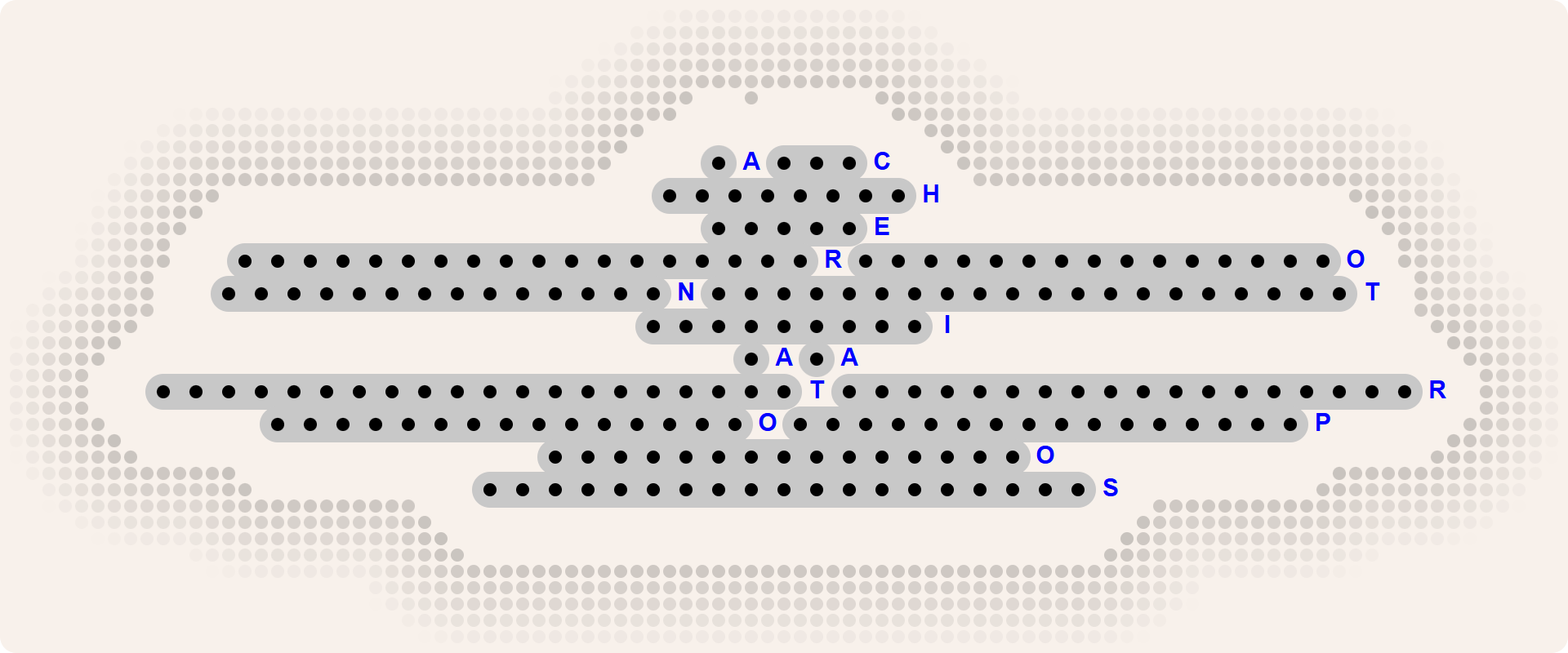
What do you see in this inkblot?

Show answer

If you recognized some winged insect, our cipher has served its purpose. The width of a continuous horizontal line (indicated by a sequence of consecutive black circles in the figure below) corresponds to a letter: A=1, B=2, C=3, .... The top horizontal line contains 20 black circles and thus represents the letter T as the 20th letter of the alphabet. The second horizontal line contains 18 black circles and represents the letter R. The third horizontal line is interrupted twice and thus consists of three sequences: a sequence of 15 black circles (the letter O), a sequence of 7 black circles (the letter G), and another sequence of 15 black circles (the letter O).

If we string the letters corresponding to each of the sequences together, we get TROGONOPTERABROOKIANA. Rajah Brooke's birdwing (Trogonoptera brookiana) is a butterfly named in 1855 by naturalist Alfred Russel Wallace after Sir James Brooke, known as the first White Rajah⁴ of Sarawak⁵. It is the national butterfly of Malaysia⁶.

So the Rorschach⁷-like inkblot was a butterfly encoded as a butterfly.

Assignment

We use the Leptidoptera cipher to encode a plaintext consisting of letters (uppercase and lowercase) and spaces as a text file whose content, with a little imagination, looks like a black-and-white image of a butterfly, a moth or another winged insect. The ciphertext (the content of the text file) uses two characters: one representing a dark color (black) and one representing a light color (white). The plaintext is encoded in the following way:

1. A letter that is at position $$n$$ in the alphabet (A=1, B=2, C=3, ...) is encoded as $$n$$ repetitions of the dark character, without making a distinction between uppercase and lowercase letters.

2. A group of letters is the longest possible sequence of consecutive letters in the plaintext that is not interrupted by spaces. A group of letters is encoded by encoding the individual letters in the group, and separating these encodings by a single light character.

3. The lines of the text file are formed by the encodings of successive groups of letters in the plaintext. Each line contains the same number of characters. This number $$m$$$ is equal to the number of characters in the longest encoding of a group of letters in the plaintext. If the encoding of a group of letters consists of less than $$m$$ characters, it is evenly supplemented by leading and trailing light characters. If an odd number of characters must be supplemented, then one more light character is supplemented at the back than at the front.

For example, suppose we want to encode this plaintext

T r ogo nop ter a b r oo k i ana

with a hash (#) as the dark color and a hyphen (-) as the light color. The plaintext has a total of 12 groups of letters. The first group of letters T is encoded as 20 hashes.

####################

The second group of letters r is encoded as 18 hashes.

##################

The third group of letters ogo is encoded as 15 hashes (the letter o is the fifteenth letter of the alphabet) followed by a hyphen, 7 hashes, a hyphen, and another 15 hashes.

###############-#######-###############

The fourth group of letters nop is encoded as 14 hashes followed by a hyphen, 15 hashes, a hyphen, and 16 hashes.

##############-###############-################

With 47 characters, this is also the longest encoding of any group of letters in the plaintext (we only know this once we have encoded all groups of letters, but take it from us). This immediately gives us the fourth line of the text file.

Since the encoding of the first group of letters only consists of 20 characters, we need to supplement it with 27 hyphens to get the first line of 47 characters. So we complete the encoding of the first group of letters with 13 leading hyphens and 14 trailing hyphens.

-------------####################--------------

If we similarly supplement the encodings of all 12 groups of letters to 47 characters, the text file contains this 12-line ciphertext (butterfly.01.txt⁸):

-------------####################--------------
--------------##################---------------
----###############-#######-###############----
##############-###############-################
-####################-#####-##################-
-----------------------#-----------------------
----------------------##-----------------------
--------------##################---------------
--------###############-###############--------
------------------###########------------------
-------------------#########-------------------
--------------#-##############-#---------------

Your task:

• Write a function decode that takes the location (str) of a text file containing a ciphertext encoded according to the Lepidoptera cipher. The function has a second optional parameter dark that takes the character (str) used as the dark color (a hash (#) is used as the dark color by default). The function has a third optional parameter light that takes the character (str) used as the light color (a space is used as the light color by default). The function must return the sequence of letters (str; in uppercase) corresponding to sequences of dark characters in the file.

• Write a function encode_group that takes a group of letters (str). The function has a second optional parameter dark that takes the character (str) used as the dark color (a hash (#) is used as the dark color by default). The function has a third optional parameter light that takes the character (str) used as the light color (a space is used as the light color by default). The function must return the encoding of the group of letters according to the Leptidoptera cipher.

• Write a function encode_groups that takes a plaintext (str) consisting of letters (uppercase and lowercase) and spaces. The function has a second optional parameter dark that takes the character (str) used as the dark color (a hash (#) is used as the dark color by default). The function has a third optional parameter light that takes the character (str) used as the light color (a space is used as the light color by default). The function must return a list containing encodings of the successive groups of letters in the plaintext according to the Leptidoptera cipher.

• Write a function supplement that takes a string $$s$$ (str). The function has a second optional parameter width that may take an integer $$m \in \mathbb{N}$$. The function has a third optional parameter character that may take a character (str; a space is used as the character by default). If no argument is passed explicitly to the parameter width or if string $$s$$ has at least $$m$$ characters, string $$s$$ itself must be returned. Otherwise string $$s$$ must be returned, evenly supplemented by leading and trailing characters. If an odd number of characters must be supplemented, then one more character is supplemented at the back than at the front.

• Write a function encode that takes a plaintext (str) consisting of letters (uppercase and lowercase) and spaces. The function has a second optional parameter dark that takes the character (str) used as the dark color (a hash (#) is used as the dark color by default). The function has a third optional parameter light that takes the character (str) used as the light color (a space is used as the light color by default). The function has a fourth optional parameter file that takes the location (str) of a text file. The function must write the encoding of the plaintext according to the Leptidoptera cipher to the file (fourth argument). If no file location is passed explicitly to the parameter file,  the function must print the encoding of the plaintext.

Example

In the following interactive session, we assume the current directory contains the text files butterfly.01.txt⁹ and butterfly.02.txt¹⁰.

>>> decode('butterfly.01.txt11', light='-')
'TROGONOPTERABROOKIANA'
>>> decode('butterfly.02.txt12', dark='X', light='_')
'ACHERONTIAATROPOS'

>>> encode_group('A')
'#'
>>> encode_group('BC', dark='X')
'XX XXX'
>>> encode_group('DEF', dark='@', light='_')
'@@@@_@@@@@_@@@@@@'
>>> encode_group('GHIJ', light='1', dark='8')
'8888888188888888188888888818888888888'

>>> encode_groups('A BC')
['#', '## ###']
>>> encode_groups('DEF GHIJ', dark='X')
['XXXX XXXXX XXXXXX', 'XXXXXXX XXXXXXXX XXXXXXXXX XXXXXXXXXX']
>>> encode_groups(' a  bc   def    ', dark='@', light='_')
['@', '@@_@@@', '@@@@_@@@@@_@@@@@@']

>>> supplement('spam')
'spam'
>>> supplement('eggs', width=10)
'   eggs   '
>>> supplement('bacon', width=10, character='_')
'__bacon___'

>>> encode('AAAAAA BBBB CCC')
# # # # # #
## ## ## ##
### ### ###
>>> encode('  aaa  bbb  ccc  ', light='_')
___#_#_#___
_##_##_##__
###_###_###
>>> encode('GH IJK LM', dark='@', light='-')
--------@@@@@@@-@@@@@@@@--------
@@@@@@@@@-@@@@@@@@@@-@@@@@@@@@@@
---@@@@@@@@@@@@-@@@@@@@@@@@@@---
>>> encode('T r ogo nop ter a b r oo k i ana', light='-')
-------------####################--------------
--------------##################---------------
----###############-#######-###############----
##############-###############-################
-####################-#####-##################-
-----------------------#-----------------------
----------------------##-----------------------
--------------##################---------------
--------###############-###############--------
------------------###########------------------
-------------------#########-------------------
--------------#-##############-#---------------
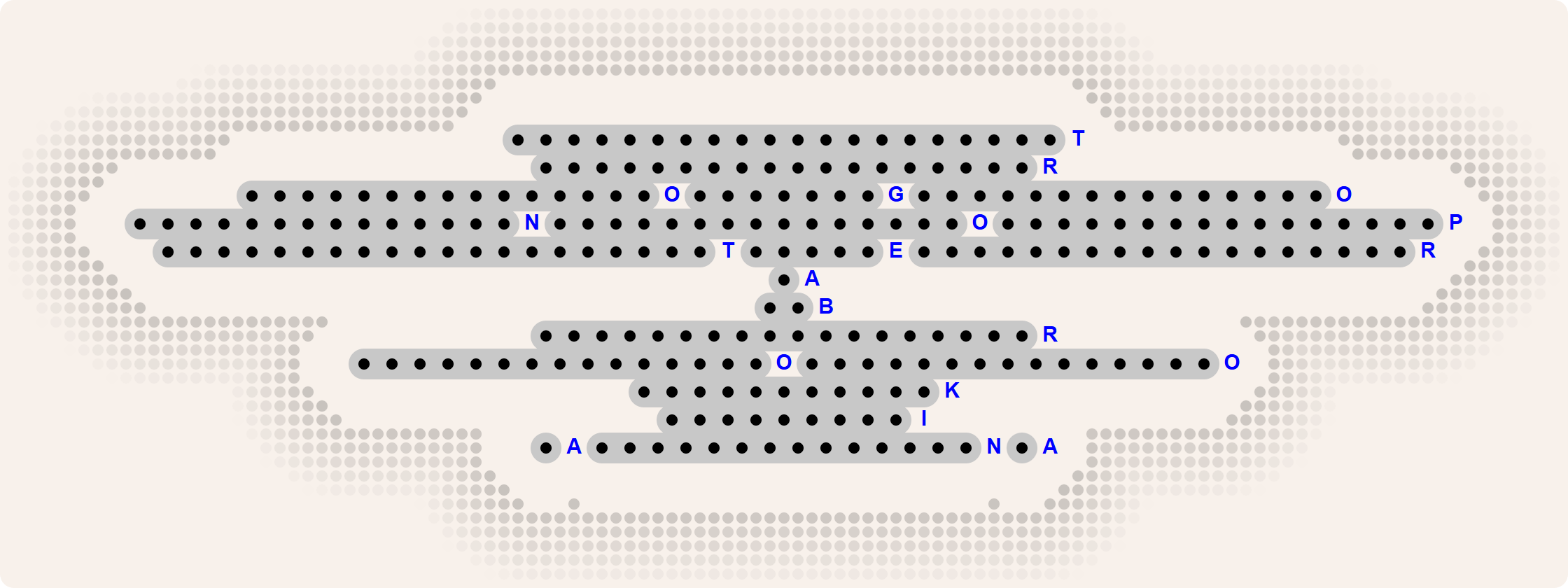
>>> encode('Ac h e ro nt i aa tr op o s', dark='X', light='_', file='ciphertext.02.txt')

Text file butterfly.01.txt¹³ corresponds to the puzzle from the introduction of this assignment. Text file butterfly.02.txt¹⁴ corresponds to this puzzle. Click here to see the solutionClick here to hide the solution.