There is one remarkable thing about randomness: its existence is neither proved nor disproved, notwithstanding the fact that it even appears everyday in science and in our everyday lives. For example, consider the constant number $$\pi$$: this number has an infinite number of decimal places with no recognizable pattern within the sequence. However, the distribution of the 10 possible digits is quite uniformly balanced — at least if we make a visual representation of, for example, the first million positions after the comma.

Generating such a visual representation is done in a fairly easy way. We always start in the origin $$(0, 0)$$. Then we walk through the digits of the number from left to right. For each digit $$c$$ we turn clockwise in a direction that makes an angle of $$c \times 36°$$ relative to the positive Y-axis and take a step of length one forward. This is illustrated in the following figure for the first ten digits of the constant number $$\pi$$.
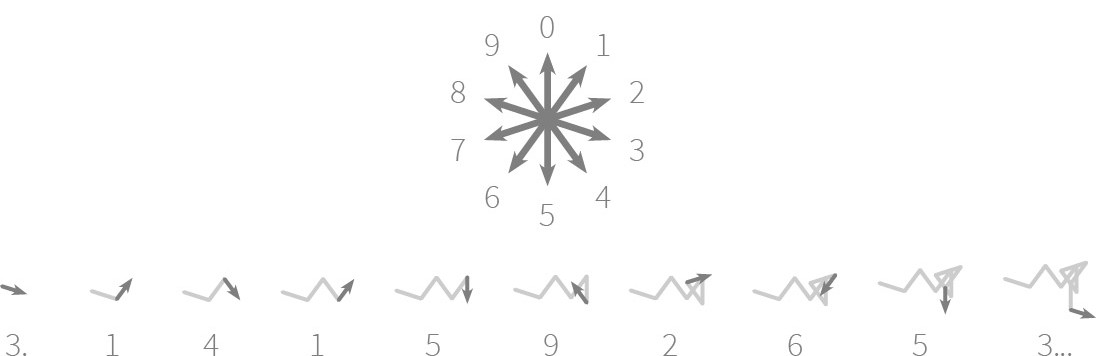
Representations of these kind of random walks are interesting for people who want to know more about the mystic character of this invisible companion. The first time they came to existence in 2009 in the masters thesis of Daniel A. Becke1r, and were refined later on in the Art in Pi2 project of Nadieh Bremer and the Number Walks3 project of Nicholas Rougeux. The work of this latter artist on a number of well known mathematical constants and irrational numbers like $$\pi$$, $$e$$ and the golden ratio have been bundled in the following sequence of video fragments.
Input
A single line that contains some text.
Output
A single line that contains the text Number g walks to position (x, y)., where g must be filled up with the given input text. The placeholders x and y must be filled up with the $$(x, y)$$-coordinates of the final position that is reached if we start in the origin, traverse all digits in the given input text from left to right, and for each digit take a step of length one in the direction described in the introduction. Both coordinates must be rounded up to two digits after the comma.
Example
Input:
3.141592653Output:
Number 3.141592653 walks to position (3.44, -1.50).Epilogue: Feynman point
A sequence of six nines occurs in the decimal representation of $$\pi$$, starting at the 762nd decimal place. It has become famous because of the mathematical coincidence and because of the idea that one could memorize the digits of $$\pi$$ up to that point, recite them and end with "nine nine nine nine nine nine and so on", which seems to suggest that $$\pi$$ is rational. The earliest known mention of this idea occurs in Douglas Hofstadter's 1985 book Metamagical Themas, where Hofstadter states
I myself once learned 380 digits of $$\pi$$, when I was a crazy high-school kid. My never-attained ambition was to reach the spot, 762 digits out in the decimal expansion, where it goes "999999", so that I could recite it out loud, come to those six 9's, and then impishly say, "and so on!"
The sequence of six nines is sometimes called the Feynman point after physicist Richard Feynman, who has also been claimed to have stated this same idea in a lecture. It is not clear when, or even if, Feynman made such a statement, however. It is not mentioned in published biographies or in his autobiographies and unknown to his biographer James Gleick.
