Intervalschatters

In de vorige sectie hebben we vastgesteld dat het steekproefgemiddelde van steekproef tot steekproef varieert rond het populatiegemiddelde dat we willen schatten. Om die reden wensen we in deze sectie een interval rond het steekproefgemiddelde te bepalen waarbinnen we het populatiegemiddelde met gegeven kans (bvb. 95% kans) kunnen verwachten. In Sectie 5.4.1 zullen we dit uitwerken voor het geval waar de populatievariantie \(\sigma^2\) op de metingen gekend is. Deze onderstelling is meestal onredelijk[28], maar wordt hier gemaakt om redenen van eenvoud. In Sectie 5.4.2 zullen we van deze onderstelling afstappen.

Gekende variantie op de metingen

Wanneer de individuele observaties \(X\) Normaal verdeeld zijn met gemiddelde \(\mu\) en gekende variantie \(\sigma^2\), noteren we dat als volgt: \(X\sim N(\mu,\sigma^2)\). Uit vorige sectie volgt dan dat het steekproefgemiddelde \(\bar{X}\) eveneens Normaal verdeeld is volgens \(N(\mu,\sigma^2/n)\). Een 95% referentie-interval voor het steekproefgemiddelde ziet er bijgevolg uit als

Het bevat met 95% kans het steekproefgemiddelde van een lukrake steekproef. Dit interval kunnen we niet expliciet berekenen op basis van de geobserveerde gegevens, omdat \(\mu\) ongekend is (we gaan er hier voorlopig van uit dat \(\sigma\) wel gekend is). Het kan wel geschat worden als

Hoewel dit laatste interval nog steeds kan geïnterpreteerd worden als een referentie-interval voor het steekproefgemiddelde, kunnen we er een veel nuttigere interpretatie aan geven. Immers, de ongelijkheid \(\mu - 1.96 \ \sigma/\sqrt{n} < \bar{X}\) kan equivalent worden herschreven als \(\mu < \bar{X} + 1.96 \ \sigma/\sqrt{n}\). Hieruit volgt:

Dit leidt tot volgende definitie.

Definitie 24 (95% betrouwbaarheidsinterval voor populatiegemiddelde)

Het interval

bevat met 95% kans het populatiegemiddelde \(\mu\). Het wordt een 95% betrouwbaarheidsinterval (in het Engels: 95% confidence interval) voor het populatiegemiddelde \(\mu\) genoemd. De kans dat het de populatieparameter \(\mu\) bevat, d.i. 95%, wordt het betrouwbaarheidsniveau genoemd.

Einde definitie

Een 95% betrouwbaarheidsinterval bepaalt met andere woorden een reeks waarden waarbinnen de gezochte populatieparameter waarschijnlijk (namelijk met 95% kans) valt.

Stel dat we in een steekproef een bloeddrukdaling van -18.93mmHg observeren en dat we weten dat de standaarddeviatie van de bloeddrukmetingen 9mmHg bedraagt. Dan vinden we een betrouwbaarheidsinterval voor de gemiddelde bloeddrukdaling van

De reden waarom over “95% kans” gesproken wordt, is omdat de eindpunten van het 95% betrouwbaarheidsinterval toevalsveranderlijken zijn die variëren van steekproef tot steekproef. Met andere woorden, verschillende steekproeven leveren telkens andere betrouwbaarheidsintervallen op, vermits die intervallen berekend zijn op basis van de gegevens in de steekproef. Men noemt het om die reden stochastische intervallen. Voor 95% van alle steekproeven zal het berekende 95% betrouwbaarheidsinterval de gezochte waarde van de populatieparameter bevatten, en voor de overige 5% niet. Dat wordt geïllustreerd a.d.h.v. een simulatiestudie in Sectie 5.4.3 (nadat we de intervallen hebben uitgebreid voor de meer realistische setting waarbij de variantie in de populatie ongekend is).

Uiteraard kunnen de onderzoekers o.b.v. een gegeven betrouwbaarheidsinterval niet besluiten of het de gezochte parameterwaarde bevat of niet, vermits ze precies op zoek zijn naar die onbekende waarde. Maar ze gebruiken een procedure die in 95% van de gevallen werkt; m.a.w. die in 95% van de gevallen de gezochte waarde bevat. Of nog, als men dagelijks gegevens zou verzamelen en telkens een 95% betrouwbaarheidsinterval zou berekenen voor een nieuwe parameter \(\theta\) (bvb. een odds ratio), dan zou men op lange termijn in 95% van de gevallen de gezochte waarde omvat hebben.

Tot nog toe zijn we ervan uitgegaan dat de individuele observaties Normaal verdeeld zijn en dat hun variantie gekend is (want als de variantie \(\sigma^2\) niet gekend is, kan men de grenzen van het interval niet berekenen). Wegens de Centrale Limietstelling bevat Vergelijking (1) het gemiddelde \(\mu\) bij benadering met 95% kans wanneer de steekproef groot is en de variantie van de individuele observaties gekend, maar hun verdeling ongekend is.

Wanneer bovendien de variantie ongekend is, kan me ze schatten door gebruik te maken van de steekproefvariantie \(S^2\) van de reeks observaties \(X_1,...,X_n\). Men kan aantonen dat het interval \([\bar{X} - 1.96 \ s/\sqrt{n} , \bar{X} + 1.96 \ s/\sqrt{n} ]\) dan het populatiegemiddelde met bij benadering 95% kans bevat, op voorwaarde dat de steekproef groot is. In de volgende sectie gaan we na hoe een betrouwbaarheidsinterval voor het populatiegemiddelde geconstrueerd kan worden wanneer de variantie ongekend is en de steekproef relatief klein.

NHANES log2 cholesterol voorbeeld

1 steekproef

set.seed(3146)
samp50 <- sample(fem$DirectChol,50)

ll <- mean(samp50 %>% log2) - 1.96*sd(samp50 %>% log2)/sqrt(50)
ul <- mean(samp50 %>% log2) + 1.96*sd(samp50 %>% log2)/sqrt(50)
popMean <- mean(fem$DirectChol%>%log2)

c(ll=ll,ul=ul,popMean=popMean)

##        ll        ul   popMean 
## 0.4326245 0.6291622 0.5142563

Bij 1 steekproef ligt het populatie gemiddelde binnen het BI of niet.

Herhaalde steekproeven

res$ll <- res$mean-1.96*res$se
res$ul <- res$mean+1.96*res$se
mu <- fem$DirectChol%>%
  log2%>%
  mean

res$inside<- res$ll <= mu & mu <= res$ul
res$n <- as.factor(res$n)
res %>%
  group_by(n) %>%
  summarize(coverage=mean(inside)) %>%
  spread(n,coverage)

## # A tibble: 1 × 3
##    `10`  `50` `100`
##   <dbl> <dbl> <dbl>
## 1  0.92 0.942 0.954

• Merk op dat de omvang in de steekproeven met 10 waarnemingen te laag is omdat we geen rekening houden met de onzekerheid in de schatting van de standaarddeviatie.

• Als we kijken naar de eerste 20 intervallen, bevat 1 van de 20 niet het populatiegemiddelde.

res %>%
  filter(n==10) %>%
  slice(1:20) %>%
  ggplot(aes(x = sample,y = mean,color = inside)) +
  geom_point() +
  geom_errorbar(aes(ymin = mean-1.96*se,ymax = mean+1.96*se))+
  geom_hline(yintercept = fem$DirectChol %>% log2 %>% mean) +
  ggtitle("20 CI for N = 10") +
  ylim(range(fem$DirectChol %>% log2))

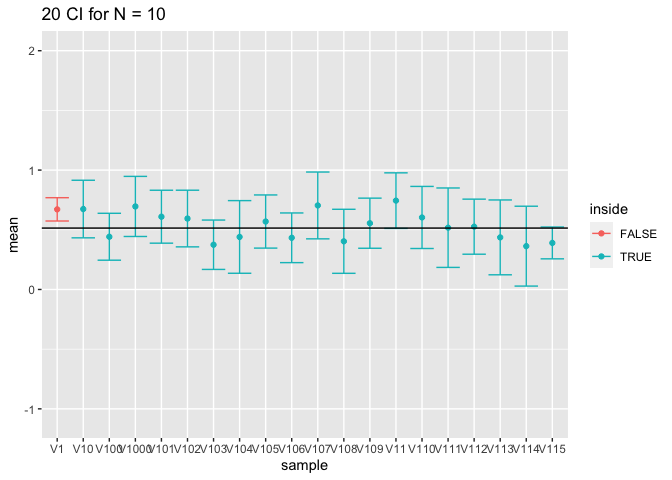
• Voor grote steekproeven (100) is de omvang prima omdat we de standaarddeviatie met een relatief hoge precisie kunnen schatten.

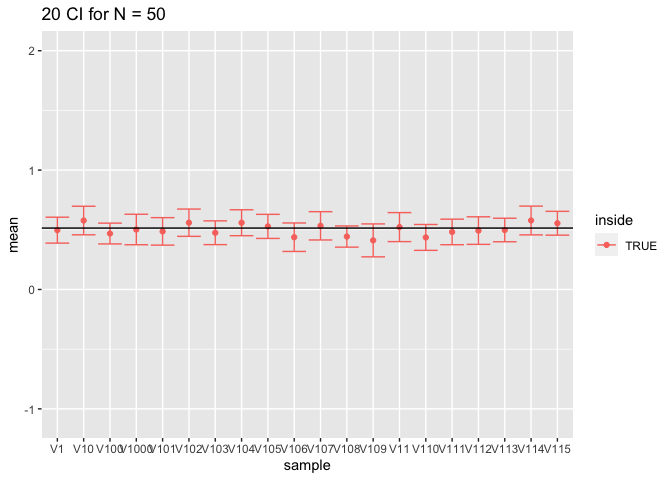
res %>%
  filter(n == 50) %>%
  slice(1:20) %>%
  ggplot(aes(x = sample,y = mean,color = inside)) +
  geom_point() +
  geom_errorbar(aes(ymin = mean-1.96*se,ymax = mean+1.96*se))+
  geom_hline(yintercept = fem$DirectChol %>% log2 %>% mean) +
  ggtitle("20 CI for N = 50") +
  ylim(range(fem$DirectChol %>% log2))

res %>%
  filter(n == 100) %>%
  slice(1:20) %>%
  ggplot(aes(x = sample,y = mean,color = inside)) +
  geom_point() +
  geom_errorbar(aes(ymin = mean-1.96*se,ymax = mean+1.96*se))+
  geom_hline(yintercept = fem$DirectChol %>% log2 %>% mean) +
  ggtitle("20 CI for N = 100") +
  ylim(range(fem$DirectChol %>% log2))

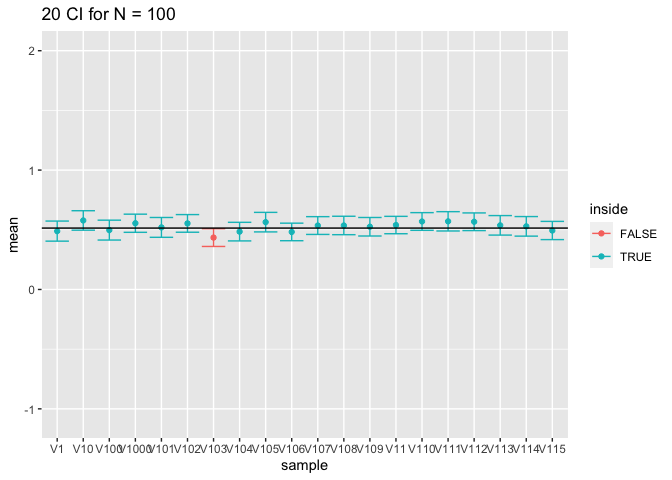
• Wat heb je geobserveerd voor de intervalbreedte?

Andere betrouwbaarheidsniveaus

Om een betrouwbaarheidsinterval met een ander betrouwbaarheidsniveau, \((1- \alpha)100\%\) te construeren, vervangt men 1.96 door het relevante kwantiel \(z_{\alpha/2}.\)

De breedte van een \(100\%(1-\alpha)\) betrouwbaarheidsinterval voor een populatiegemiddelde \(\mu\) is \(2 z_{\alpha/2} \ \sigma/\sqrt{n}\). Ze wordt dus bepaald door 3 factoren: de standaarddeviatie op de individuele observaties, \(\sigma\), de grootte van de steekproef, \(n\), en het betrouwbaarheidsniveau, \(1-\alpha\):

• \(n\): naarmate de steekproefgrootte toeneemt, krimpt het betrouwbaarheidsinterval. In grote steekproeven beschikken we immers over veel informatie en kunnen we de gezochte populatieparameter bijgevolg relatief nauwkeurig afschatten.

• \(\sigma\): naarmate de standaarddeviatie van de oorspronkelijke observaties toeneemt, neemt de lengte van het betrouwbaarheidsinterval toe. Indien er immers veel ruis op de gegevens zit, dan is het moeilijker om populatieparameters of -kenmerken te identificeren.

• \(1-\alpha\): naarmate het betrouwbaarheidsniveau toeneemt, wordt het betrouwbaarheidsinterval breder. Indien we immers eisen dat het interval met 99.9% kans de populatiewaarde bevat i.p.v. met 80% kans, dan zullen we duidelijk een breder interval nodig hebben.

Betrouwbaarheidsintervallen worden niet enkel gebruikt voor het populatiegemiddelde, maar kunnen in principe voor om het even welke populatieparameter worden gedefinieerd. Zo kunnen ze bijvoorbeeld gedefinieerd worden voor een verschil tussen 2 gemiddelden, voor een odds ratio, voor een variantie, … De manier om die intervallen te berekenen is vaak complex en sterk afhankelijk van de gebruikte schatter voor de populatieparameter. Er wordt daarom niet van u verwacht dat u voor alle populatieparameters die we in deze cursus ontmoeten, een betrouwbaarheidsinterval kunt berekenen, maar wel dat u het kunt interpreteren.

Definitie 25 (Betrouwbaarheidsinterval)

Een \((1-\alpha)100\)% betrouwbaarheidsinterval voor een populatieparameter \(\theta\) is een geschat (en bijgevolg stochastisch) interval dat met \((1-\alpha)100\)% kans de echte waarde van die populatieparameter \(\theta\) bevat.

Einde Definitie