Akari is een Japanse puzzel die gespeeld wordt op een rechthoekig rooster met witte en zwarte cellen.

Een opgave van een akari op een $$6 \times 6$$ rooster.

Het doel is om lampen in de witte cellen te plaatsen zodat twee lampen nooit rechtstreeks op elkaar schijnen en zodat het volledige spelbord verlicht wordt.

De oplossing van de akari op een $$6 \times 6$$ rooster.

Daarbij zendt een lamp horizontaal en verticaal lichtstralen uit, en verlicht de hele rij en kolom waarop de lamp staat, tenzij het licht geblokkeerd wordt door een zwarte cel.

Een lamp zendt horizontaal en verticaal lichtstralen uit, en verlicht de hele rij en kolom waarop de lamp staat, tenzij het licht geblokkeerd wordt door een zwarte cel.

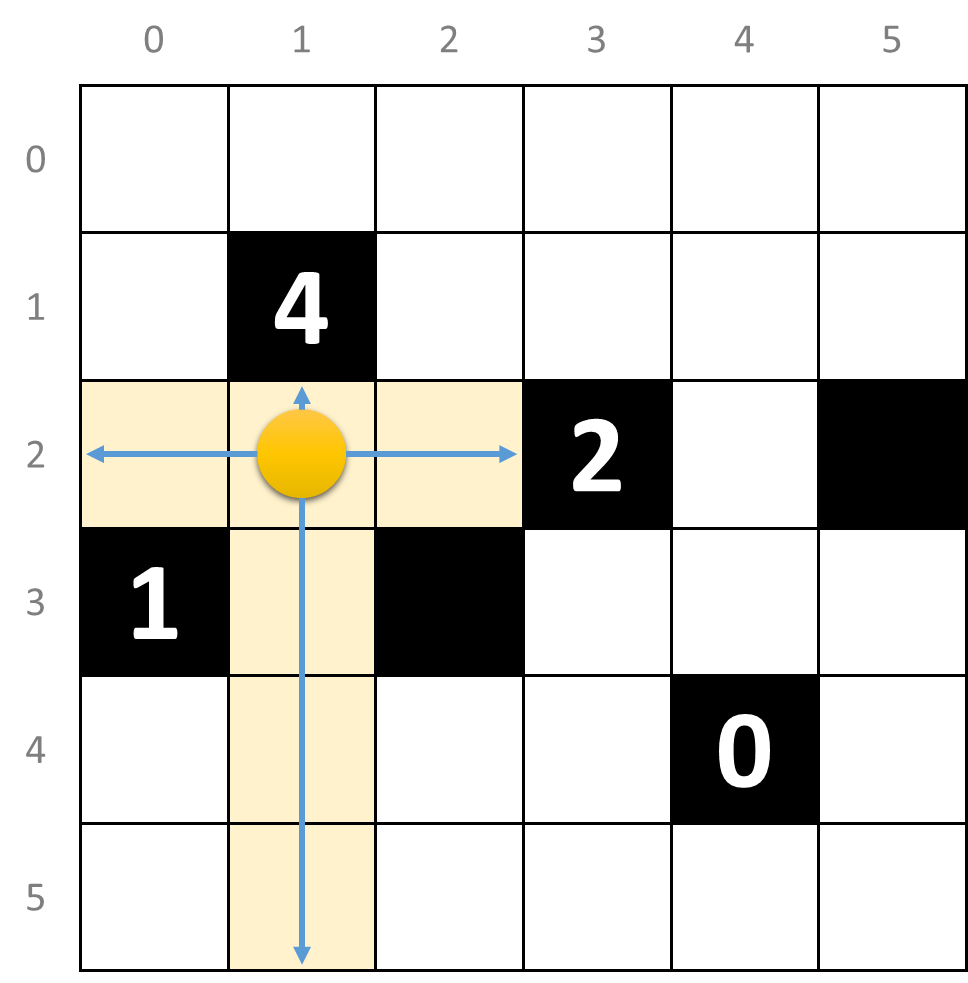
Een zwarte cel kan gemarkeerd zijn met een getal van 0 tot 4. Dat getal geeft aan hoeveel lampen op horizontaal of verticaal aangrenzende witte cellen rondom de zwarte cel moeten geplaatst worden: een zwarte cel met een 4 moet bijvoorbeeld omgeven worden door 4 lampen, en rondom een zwarte cel met een 0 mogen geen lampen geplaatst worden. Rondom een zwarte cel zonder getal kan een willekeurig aantal lampen geplaatst worden. Lampen die schuin naast een genummerde zwarte cel staan, dragen niet bij aan het aantal lampen rondom die cel. De lampen hoeven ook niet per se aan een zwarte cel te grenzen.

Opgave

Om te kunnen verwijzen naar een cel in het rechthoekig rooster van een akaripuzzel worden de rijen van boven naar onder genummerd, en de kolommen van links naar rechts, telkens vanaf nul. Daardoor kan de positie van een cel voorgesteld worden als een tuple $$(r, k)$$, waarbij $$r \in \mathbb{N}$$ (int) het rijnummer en $$k \in \mathbb{N}$$ (int) het kolomnummer aanduidt.

De configuratie van de zwarte cellen in het rooster van een akaripuzzel wordt opgeslaan in een tekstbestand. Elke regel van het bestand bevat drie eigenschappen van een zwarte cel, van elkaar gescheiden door een spatie: i) het rijnummer $$r$$, ii) het kolomnummer $$k$$ en iii) de markering. De markering is een getal van 0 tot 4, of een vraagteken (?) als de cel niet gemarkeerd is. Het volgende tekstbestand beschrijft bijvoorbeeld de zwarte cellen in de opgave uit de inleiding.

Definieer een klasse Akari waarmee het rooster van akaripuzzels kan voorgesteld worden. Bij het aanmaken van een akaripuzzel (Akari) moeten drie argumenten doorgegeven worden: i) het aantal rijen (int) van het rooster, ii) het aantal kolommen (int) van het rooster, en iii) de locatie (str) van een tekstbestand met de configuratie van de zwarte cellen in het rooster. Elke akaripuzzel (Akari) moet minstens de volgende eigenschappen hebben:

zwarte_cellen: een dictionary (dict) die de positie van elke zwarte cel in het rooster afbeeldt op de markering (str) van die cel; de voorstelling van de markeringen is dezelfde als in het tekstbestand
lampen: een verzameling (set) met de posities van alle lampen in het rooster

Daarnaast moeten akaripuzzels (Akari) minstens ook de volgende methoden ondersteunen:

Een methode plaats_lamp waaraan het rijnummer $$r$$ en het kolomnummer $$k$$ van een positie in het rooster moet doorgegeven worden. De methode moet nagaan of op positie $$(r, k)$$ een lamp kan geplaatst worden. Dat is het geval als aan de volgende voorwaarden voldaan is

positie $$(r, k)$$ valt binnen het rooster
de cel op positie $$(r, k)$$ is wit
de cel op positie $$(r, k)$$ is nog niet bezet door een andere lamp
de cel op positie $$(r, k)$$ wordt niet verlicht door een andere lamp
alle genummerde zwarte cellen die aan positie $$(r, k)$$ grenzen kunnen nog omgeven worden door minstens één bijkomende lamp

Als minstens één van deze voorwaarden niet voldaan is, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige positie. Anders moet het object bijhouden dat er op positie $$(r, k)$$ een lamp geplaatst werd.

Een methode verwijder_lamp waaraan het rijnummer $$r$$ en het kolomnummer $$k$$ van een positie in het rooster moet doorgegeven worden. De methode moet de lamp die op positie $$(r, k)$$ staat terug verwijderen. Als er op positie $$(r, k)$$ geen lamp staat dan moet een AssertionError opgeworpen worden met de boodschap ongeldige positie.
Een methode stralen waaraan het rijnummer $$r$$ en het kolomnummer $$k$$ van een positie in het rooster moet doorgegeven worden. De methode moet een verzameling (set) teruggeven met alle posities die zouden verlicht worden als er een lamp op positie $$(r, k)$$ zou geplaatst worden. Daarbij maakt het niet uit of de cel op positie $$(r, k)$$ wit of zwart is (doe alsof het een witte cel met een lamp is). De positie $$(r, k)$$ mag zelf niet in de verzameling opgenomen worden (de lamp staat op de cel en daardoor wordt de cel zelf niet door de lamp verlicht).
Een methode verlicht waaraan geen argumenten moeten doorgegeven worden. De methode moet een verzameling (set) teruggeven met de posities van alle vrije witte cellen in het rooster die door een lamp verlicht worden.
Een methode isopgelost waaraan geen argumenten moeten doorgegeven worden. De methode moet een Booleaanse waarde (bool) teruggeven die aangeeft of de akaripuzzel correct opgelost werd. Dat is het geval als alle vrije witte cellen door een lamp verlicht worden én als alle genummerde zwarte cellen omgeven worden door het gegeven aantal lampen.

Als een akaripuzzel (Akari) wordt doorgegeven aan de ingebouwde functie str, dan moet een stringvoorstelling (str) van het rooster teruggegeven worden. Daarin vormt elke rij een afzonderlijke regel, worden zwarte cellen voorgesteld door hun markering (zelfde voorstelling als in het tekstbestand), witte cellen waarop een lamp staat door de hoofdletter L, witte cellen die door minstens één lamp verlicht worden door een asterisk (*) en alle andere witte cellen door een underscore (_).

Voorbeeld

        >>> puzzel = Akari(6, 6, 'akari.txt')
>>> puzzel.zwarte_cellen
{(1, 1): '4', (2, 3): '2', (2, 5): '?', (3, 0): '1', (3, 2): '?', (4, 4): '0'}
>>> puzzel.lampen
set()
>>> puzzel.verlicht()
set()
>>> print(puzzel)
______
_4____
___2_?
1_?___
____0_
______
>>> puzzel.isopgelost()
False
>>> puzzel.stralen(1, 1)
{(0, 1), (1, 2), (1, 3), (3, 1), (2, 1), (1, 4), (1, 5), (5, 1), (1, 0), (4, 1)}
>>> puzzel.stralen(2, 1)
{(3, 1), (2, 0), (2, 2), (5, 1), (4, 1)}
>>> puzzel.plaats_lamp(2, 1)
>>> puzzel.lampen
{(2, 1)}
>>> puzzel.verlicht()
{(2, 0), (2, 2), (5, 1), (3, 1), (4, 1)}
>>> print(puzzel)
______
_4____
*L*2_?
1*?___
_*__0_
_*____
>>> puzzel.isopgelost()
False
>>> puzzel.plaats_lamp(3, 6)          # buiten rooster
Traceback (most recent call last):
AssertionError: ongeldige positie
>>> puzzel.plaats_lamp(1, 1)          # niet op witte cel
Traceback (most recent call last):
AssertionError: ongeldige positie
>>> puzzel.plaats_lamp(2, 1)          # cel bevat al een lamp
Traceback (most recent call last):
AssertionError: ongeldige positie
>>> puzzel.plaats_lamp(5, 1)          # cel wordt verlicht door andere lamp
Traceback (most recent call last):
AssertionError: ongeldige positie
>>> puzzel.plaats_lamp(4, 5)          # te veel lampen naast zwarte cel
Traceback (most recent call last):
AssertionError: ongeldige positie
>>> puzzel.plaats_lamp(0, 1)
>>> puzzel.plaats_lamp(1, 0)
>>> puzzel.plaats_lamp(1, 2)
>>> puzzel.lampen
{(0, 1), (1, 0), (2, 1), (1, 2)}
>>> puzzel.verlicht()
{(0, 0), (1, 3), (2, 2), (3, 1), (1, 4), (2, 0), (1, 5), (0, 5), (0, 4), (5, 1), (0, 3), (4, 1), (0, 2)}
>>> print(puzzel)
*L****
L4L***
*L*2_?
1*?___
_*__0_
_*____
>>> puzzel.isopgelost()
False
>>> puzzel.verwijder_lamp(1, 2)
>>> puzzel.lampen
{(0, 1), (1, 0), (2, 1)}
>>> print(puzzel)
*L****
L4____
*L*2_?
1*?___
_*__0_
_*____
>>> puzzel.plaats_lamp(1, 2)
>>> print(puzzel)
*L****
L4L***
*L*2_?
1*?___
_*__0_
_*____
>>> puzzel.verwijder_lamp(2, 2)
Traceback (most recent call last):
AssertionError: ongeldige positie
>>> puzzel.plaats_lamp(2, 4)
>>> puzzel.plaats_lamp(3, 3)
>>> puzzel.plaats_lamp(4, 0)
>>> puzzel.plaats_lamp(5, 5)
>>> puzzel.lampen
{(0, 1), (1, 2), (3, 3), (5, 5), (2, 1), (1, 0), (2, 4), (4, 0)}
>>> puzzel.verlicht()
{(5, 4), (0, 0), (1, 3), (4, 1), (4, 5), (5, 2), (1, 4), (0, 5), (5, 1), (0, 3), (4, 2), (5, 3), (3, 5), (3, 1), (1, 5), (2, 0), (0, 4), (4, 3), (2, 2), (5, 0), (3, 4), (0, 2)}
>>> print(puzzel)
*L****
L4L***
*L*2L?
1*?L**
L***0*
*****L
>>> puzzel.isopgelost()
True

Opgave

Voorbeeld

Epiloog