De wortelformule is de algemene methode om een vierkantsvergelijking op te lossen. In de volgende opdracht ga je dit omzetten naar Python code.

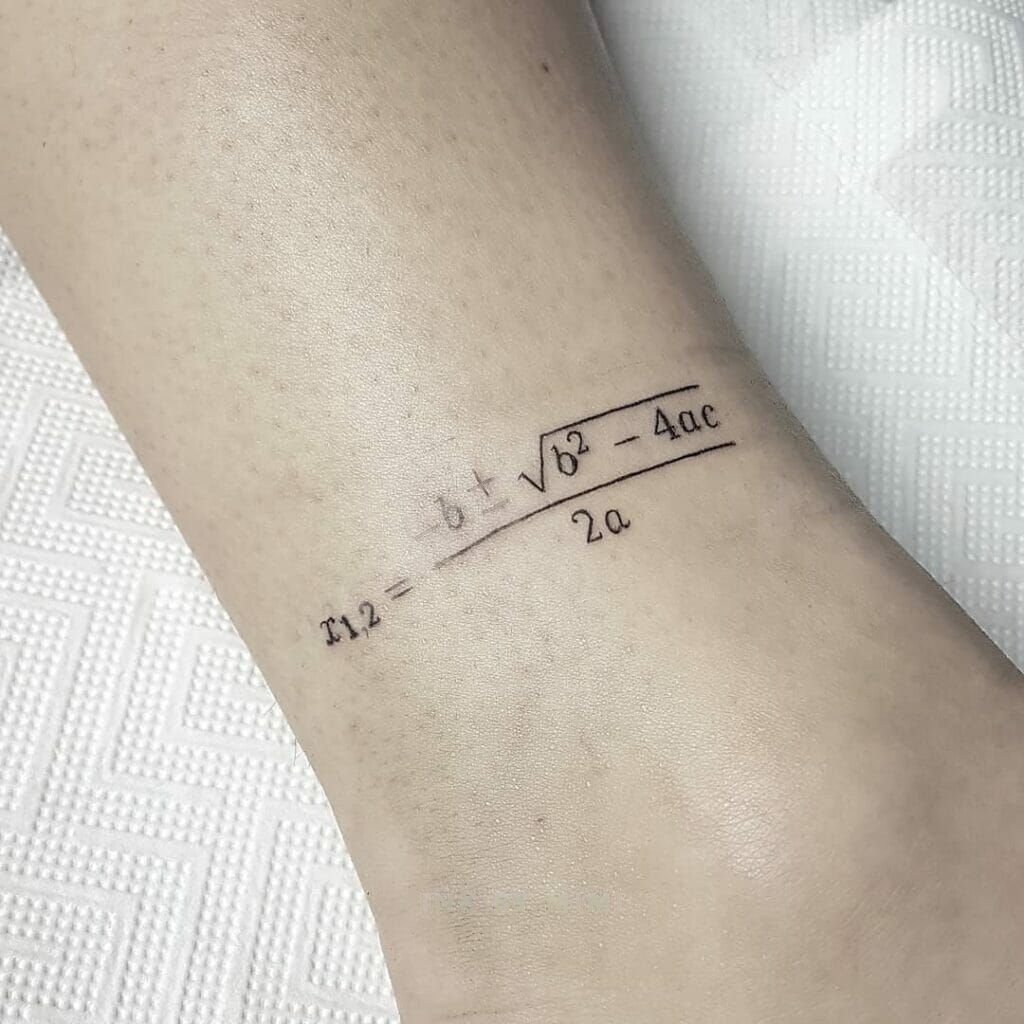
Opgave

Schrijf een functie vkv( a, b, c ) die voor een vierkantsvergelijking \(ax^2+bx+c=0\) de oplossingen berekent. De oplossingen worden op een specifieke manier afgedrukt. Het resultaat wordt afgerond op 2 cijfers na de komma (indien nodig).

Tip

Om de vierkantswortel te berekenen gebruik je math.sqrt(). Er geldt bijvoorbeeld dat math.sqrt( 36 ) gelijk is aan 6.0.

Voorbeelden

De vierkantsvergelijking \(x^2+3x-4 = 0\) heeft als oplossingenverzameling \(V = \{-4, 1\}\).

>>> vkv( 1, 3, -4 ) 
Er zijn 2 reële oplossingen, namelijk 1.0 en -4.0

De vierkantsvergelijking \(x^2+2x+1 = 0\) heeft als oplossingenverzameling \(V = \{-1\}\).

>>> vkv( 1, 2, 1 ) 
Er is één oplossing, namelijk: -1.0

De vierkantsvergelijking \(2x^2+6x+5 = 0\) heeft geen reële oplossingen.

>>> vkv( 2, 6, 5 ) 
Er zijn geen reële oplossingen