Using a 7-liter and a 3-liter jug, how can you obtain exactly 5 liters of water from a well? That's a water-fetching puzzle, a familiar task in puzzle books. Most such problems can be solved fairly easy using intuition or trial-and-error. In his book Scripta Mathematica from 1948 H.D. Grossman however describes an ingenious way to generate a solution.
Let $$a$$ and $$b$$ be the sizes of the jugs (in liter), and $$c$$ be the number of liters that we're seeking. In the example given above $$a=7$$, $$b=3$$ and $$c=5$$. The positive integers $$a$$ and $$b$$ must not be same, must be relatively prime (their greatest common divisor should be equal to 1) and the volume of at least one of the jugs needs to be larger than $$c$$ liter. Otherwise the problem is unsolvable, trivial, or can be reduced to smaller integers.

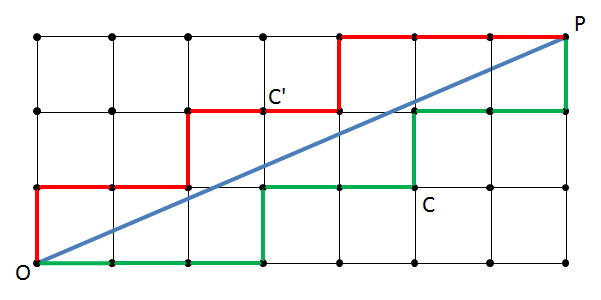
Consider a field of lattice points (points having integer coordinates) containing the line $$OP$$ (blue line) that connects $$O$$ at the point $$(0, 0)$$ with $$P$$ at the point $$(a, b)$$ (the point $$(7, 3)$$ in our example). Then draw a zigzag line $$Z$$ (green line) that starts at $$O$$ and always connects the current point with its top neighbour if this point is not above the line $$OP$$, or otherwise connects the current point with its right neighbour. It may be proved that $$Z$$ crosses the line $$OP$$ for the first time in $$P$$.
The zigzag line $$Z$$ now gives a map showing how to fill the jugs from the well, pour water from one jug in the other, and empty jugs, until a point is reached where one of the jugs exactly contains the number of liters we want to retrieve. Starting from $$O$$ and following the zigzag line, we perform the following two actions at each vertical step
Fill the $$a$$-liter jug with water from the $$b$$-liter jug.
Empty the $$a$$-liter jug. (no need to do this if the $$b$$-liter jug already contains $$c$$ liters of water)
and we perform the following two actions at each horizontal step
Pour the content of the $$b$$-liter jug in the $$a$$-liter jug. (if the $$b$$-liter jug contains water)
Fill the $$b$$-liter jug from the well. (no need to do this if the $$a$$-liter jug already contains $$c$$ liters of water)
We follow $$Z$$ until one of both jugs exactly contains the requested water volume. It may be proven that the zigzag line always contains a point $$C$$ where this condition is fulfilled. In our example, the map instructs us to
Fill the 3-liter jug from the well.
Pour the content of the 3-liter jug in the 7-liter jug.
Fill the 3-liter jug from the well.
Pour the content of the 3-liter jug in the 7-liter jug.
Fill the 3-liter jug from the well.
Fill the 7-liter jug with water from the 3-liter jug. (one more liter of water can be poured, so that the 3-liter jug still contains 2 liters of water)
Empty the 7-liter jug.
Pour the content of the 3-liter jug in the 7-liter jug. (the 7-liter jug now contains 2 liters of water)
Fill the 3-liter jug from the well.
Pour the content of the 3-liter jug in the 7-liter jug.
The 7-liter jug now contains 5 liter.
An alternate solution can be found by drawing a second zigzag line $$Z'$$ (red line) on top of $$OP$$. This line always visits the right neightbour if that point is above the line $$OP$$, otherwise it visits the top neighbour. In reading this solution, we swap the roles of $$a$$ and $$b$$ given above. In our example, the alternative map instructs us to
Fill the 7-liter jug from the well.
Fill the 3-liter jug with water from the 7-liter jug.
Empty the 3-liter jug.
Fill the 3-liter jug with water from the 7-liter jug. (remains 1 liter of water in the 7-liter jug)
Empty the 3-liter jug.
Pour the content of the 7-liter jug in the 3-liter jug. (the 3-liter jug now contains 1 liter of water)
Fill the 7-liter jug from the well.
Fill the 3-liter jug with water from the 7-liter jug. (2 liters of water are poured)
The 7-liter jug now contains 5 liter.
In his book Grossman stated that "There are always exactly two solutions which are in a sense complementary to each other."
Assignment
Write a function position that takes two points $$p_1$$ and $$p_2$$. Each point is represented as a tuple containing two integers $$(x, y)$$. The function must return an integer that indicates whether point $$p_2$$ is on (value 0), above (value 1) or below (value -1) the line that goes through the origin $$(0, 0)$$ and the point $$p_1$$.
Hint: If $$p_1$$ is the point $$(a, b)$$, the line connecting this point with the origin is described by the equation $$ay - bx = 0$$. For points $$(x, y)$$ that are above this line, the expression $$ay - bx$$ is positive, and for points that are below the line the expression is negative.Write a function wellDone that takes three integers $$a$$, $$b$$ and $$c$$. The function must print the actions needed to retrieve exactly $$c$$ liters of water using an $$a$$-liter jug and a $$b$$-liter jug. Finally, the function should also print which jug has the requested volume of water. You may assume that the positive integers $$a$$ and $$b$$ are not the same, are relatively prime and that the volume of at least one of the jugs is larger than $$c$$ liters. Make sure that your implementation of the function prints the description of the actions in exactly the same way as in the examples below. The function must also have an optional fourth parameter alternative that indicates whether the first solution (value False, the default value) or the alternative solution (value True) should be printed.
Example
>>> position((3, 7), (3, 0))
-1
>>> position((3, 7), (0, 3))
1
>>> position((3, 7), (6, 14))
0
>>> wellDone(7, 3, 5)
Fill the 3-liter jug from the well.
Pour the content of the 3-liter jug in the 7-liter jug.
Fill the 3-liter jug from the well.
Pour the content of the 3-liter jug in the 7-liter jug.
Fill the 3-liter jug from the well.
Fill the 7-liter jug with water from the 3-liter jug.
Empty the 7-liter jug.
Pour the content of the 3-liter jug in the 7-liter jug.
Fill the 3-liter jug from the well.
Pour the content of the 3-liter jug in the 7-liter jug.
The 7-liter jug now contains 5 liter.
>>> wellDone(7, 3, 5, alternative=True)
Fill the 7-liter jug from the well.
Fill the 3-liter jug with water from the 7-liter jug.
Empty the 3-liter jug.
Fill the 3-liter jug with water from the 7-liter jug.
Empty the 3-liter jug.
Pour the content of the 7-liter jug in the 3-liter jug.
Fill the 7-liter jug from the well.
Fill the 3-liter jug with water from the 7-liter jug.
The 7-liter jug now contains 5 liter.