Ghent University (UGent) was founded on October 9, 1817 in the city hall of Ghent, Belgium. Many activities were organized in 2017 to celebrate its 200^th anniversary. On this occasion, we have designed a prime number dedicated to Ghent University.

The prime number only contains the digits 1 and 8 — 9000 in total, as a reference to the postal code of Ghent, Belgium — but if you look carefully you'll also notice a single occurrence of the digit 2 in the prime number (marked in yellow in the figure above).

Assignment

The text file hidden_words.txt¹ contains a list of hidden words. Each line of the file contains a word that only consists of letters (both uppercase and lowercase letters are allowed), where we have randomly inserted some digits before, between and after the letters of the word.

We use the notation $$\mathcal{P}$$ for the set of all words that only consist of letters (both uppercase and lowercase letters are allowed), where additional digits have been inserted before, between and after the letters of the word. A longest possible sequence of letters in $$p \in \mathcal{P}$$ is called a group. Your task:

1. Determine the shortest possible regular expressions for the following subsets of $$\mathcal{P}$$:

   • $$\mathcal{P}_1 = \{\,p \in \mathcal{P}\,|\,$$ there are no digits between the letters of the word in $$p\,\}$$

     example:	39568250269955376311912572precondition005426787530581443236416842014020466976603 $$\in \mathcal{P}_1$$
     	18958535313605793170095290529923mathematici2779805995331496368099837070an1084015 $$\not\in \mathcal{P}_1$$

   • $$\mathcal{P}_2 = \{\,p \in \mathcal{P}\,|\, p$$ contains a sequence of at least three consecutive odd digits that is not interrupted by letters$$\,\}$$

     example:	28411868663721472744440442174386579246325770883aldo29349020307976l83871941955671 $$\in \mathcal{P}_2$$
     	24054592017722795066151886136772461985802800654731523434656051391micr9otechnique $$\not\in \mathcal{P}_2$$

     Note

     With consecutive odd digits we refer to the sequence 1, 3, 5, 7 and 9.

   • $$\mathcal{P}_3 = \{\,p \in \mathcal{P}\,|\, p$$ contains at least five groups$$\,\}$$

     example:	30474967583414287634529432102615285637683he6244139301523560terotr4565918op1hi15c $$\in \mathcal{P}_3$$
     	683929629607366384846442641925771941514gues230109sworks7958462277260966903049357 $$\not\in \mathcal{P}_3$$

   • $$\mathcal{P}_4 = \{\,p \in \mathcal{P}\,|\,$$first and last letter of $$p$$ are respectively preceded and followed by the same digit$$\,\}$$

     example:	9366947533557157204181560054978886808334627588608299ang0io752901403085mat93a9535 $$\in \mathcal{P}_4$$
     	39384286489764957586401269744226275965emissivi64159406666255631009ty911316262761 $$\not\in \mathcal{P}_4$$

   Each time give a Unix command where the regular expression is used by a command from the grep family to write only those lines from the text file to stdout whose pattern $$p$$ belongs to $$\mathcal{P}_i\ (i = 1, 2, 3, 4)$$.

   Note

   Make sure you use a recent version of GNU grep for this assignment. A recent version of GNU grep has been installed on helios, but Mac OS X typically uses and older version of GNU grep by default. Mac users are advised to upgrade their grep to the latest version.

2. Find the words $$w_1\ w_2\ w_3\ w_4$$ of a secret message in the following way:

   • the word $$w_1$$ is on the unique line whose pattern $$p$$ belongs to $$\mathcal{P}_1 \cap \mathcal{P_2}$$

   • the word $$w_2$$ is on the unique line whose pattern $$p$$ belongs to $$ \mathcal{P}_2 \cap \mathcal{P_3}$$

   • the word $$w_3$$ is on the unique line whose pattern $$p$$ belongs to $$\mathcal{P}_3  \cap \mathcal{P_4}$$

   • the word $$w_4$$ is on the unique line whose pattern $$p$$ belongs to $$\mathcal{P}_4 \cap \mathcal{P_1}$$

   Each time give a Unix command where the regular expressions for the subsets $$\mathcal{P}_i\ (i = 1, 2, 3, 4)$$ are used by commands from the grep family to find the word $$w_j\ (j = 1, 2, 3, 4)$$ in the text file and write it to stdout. It is not allow to write the word $$w_j$$ literally (e.g. echo $$w_j$$).

Epilogue

The design of the Ghent University prime number has been inspired by this video published by Numberphile².

The video features a startling wall hanging in the Senior Combination Room at Trinity Hall³, Cambridge. Junior research fellow James McKee devised a 1350-digit prime number whose image forms a likeness of the college's coat of arms. The number of digits is significant, as it's the year that Bishop William Bateman⁴ founded the college.

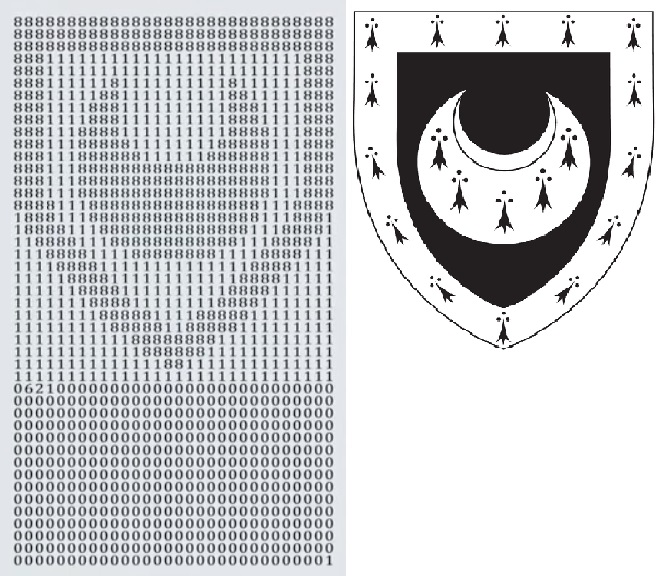
It turns out that finding such "prime" images is easier than one might think. In the video description, McKee explains:

Most of the digits of $$p$$ were fixed so that i) the top two thirds made the desired pattern and ii) the bottom third ensured that $$p - 1$$ had a nice large (composite) factor $$F$$ with the factorisation of $$F$$ known. Numbers of this shape can easily be checked for primality. A small number of digits (you can see which!) were looped over until $$p$$ was found that was prime.

This inspired Cambridge math student Jack Hodkinson to publish his own prime number, this one presenting an image⁵ of Corpus Christi College⁶ and including his initials and date of birth.

To design the Ghent University prime number, we started from the logo that was used to celebrate the 200^th anniversary of Ghent University.

This logo has then been converted into an ASCII image containing 9000 digits (as a reference to the postal code of the city of Ghent, Belgium), split over 75 rows containing 120 ones and eights each. We selected Bimini as a font to represent the prime number, because it gave good contract between the "heavy" eights (representing the blue pixels) and the "light" ones (representing the white pixels). Luckily, the bottom right pixel was white, because the prime number we had in mind could impossibly be even.

We then wrote a Python program to convert this initial number — which showed the pattern we had in mind, but wasn't a prime number yet — into a prime number. To do so, the program systematically iterated over all eights in the initial number, replaced the eight by another digit (not 1 or 8), and checked if the resulting number was prime. To quickly check if a 9000-digit number is prime, we used the Miller-Rabin primality test⁷. This algorithm is always correct in saying that a given number is not prime, but it can only state with (very) high probability that a given number is prime. To finally check that a candidate prime number was indeed prime, we used Dario Alpern's fantastic tool⁸ to give ourselves absolute certainty.

How were we so confident that this would work? Well, the prime number theorem⁹ tells us that there are approximately $$\frac{n}{\log{n}}$$ primes less than $$n$$. So there are approximately \[ \frac{10^{9000}}{\log{10^{9000}}} - \frac{10^{8999}}{\log{10^{8999}}} \approx   4.34 \times 10^{8995} \] 9000-digit primes. So, approximately one in every 21.000 9000-digit numbers is prime. Of course, we haven't calculated these estimates at the back of an envelope, as we also had Python to the rescue here (the module Decimal provides support for fast correctly-rounded decimal floating point arithmetic).

>>> from decimal import Decimal
>>> n = Decimal(10 ** 9000)
>>> m = Decimal(10 ** 8999)
>>> estimate = lambda x : x / x.ln()
>>> primes_with_9000_digits = estimate(n) - estimate(m)
>>> primes_with_9000_digits
Decimal('4.342891196471751863968210190E+8995')
>>> numbers_with_9000_digits = 9 * m
>>> numbers_with_9000_digits / primes_with_9000_digits
Decimal('20723.52171132395093158056936')

The even numbers were left out of consideration in advance, reducing half of the search space. We could also skip the digits 0, 3, 6 and 9 as replacements for one of the eights, since the combination with 7660 ones and 1339 eights would always result in a multiple of three. This only left us with the digits 2, 4, 5 and 7 that needed to be considered as replacements for one of the eights.

Searching our prime number would definitely not be as time consuming as looking for the proverbial needle in a haystack. But if you take into account that it takes a couple of minutes to figure out if a 9000-digit number is prime, it could have easily taken us more than a month to find our prime number. Luckily, we also had the Ghent University supercomputer¹⁰ at our disposal (thanks to the collaboration with the Flemish Supercomputer Centre¹¹) to check many numbers at the same time. In the end, the 2942^nd number checked turned out to be prime, so that our rudimentary prediction from above even proved to be a slight overestimation.