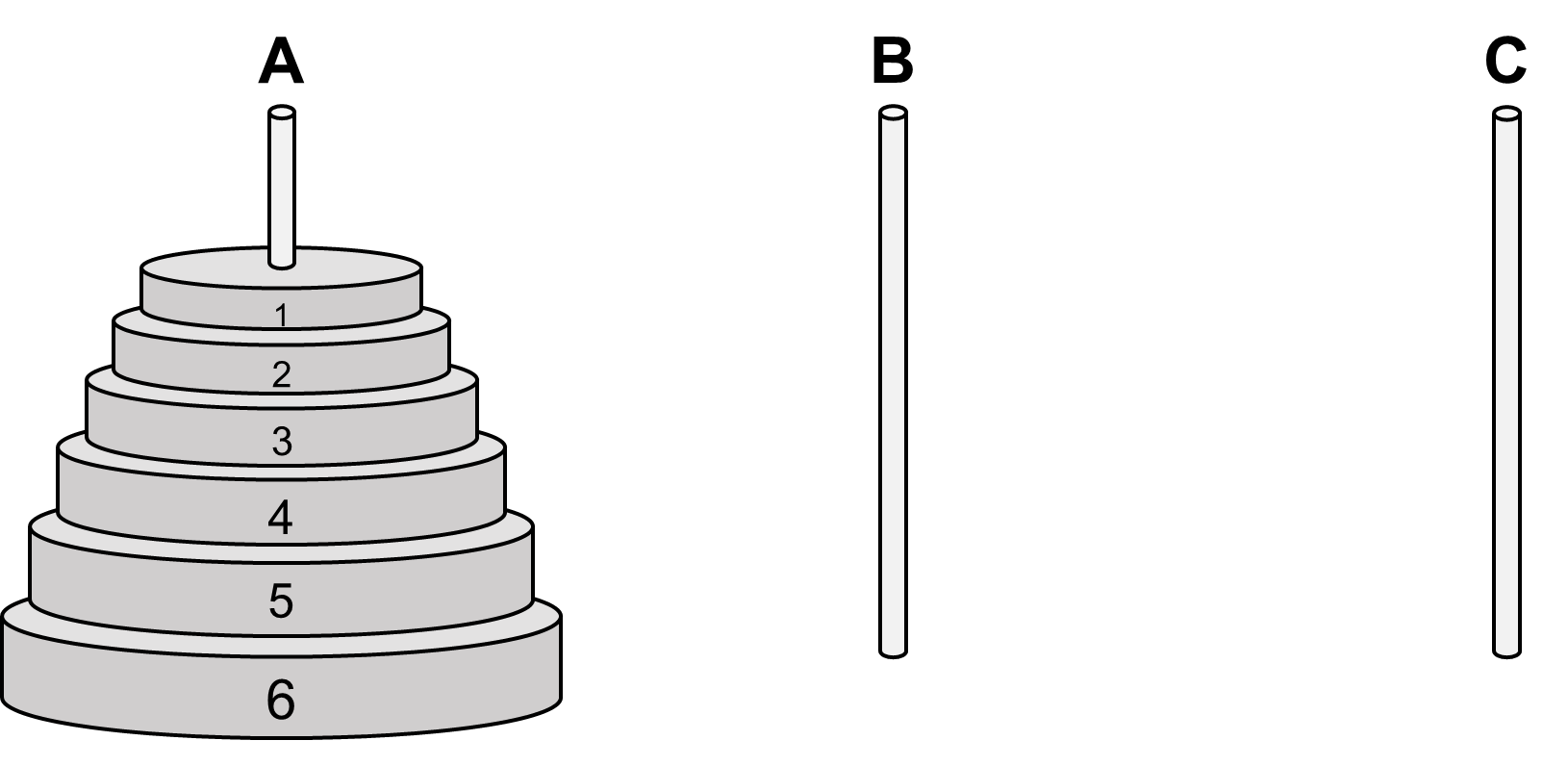
The Towers of Hanoi is a puzzle, which uses three poles, labeled A, B, and C. On pole A there is a stack of discs of varying size; the discs are numbered according to their size. The smallest disc is 1, the next one is 2, the next one is 3, etcetera, up to size \(n\). Typical values for \(n\) are 4 and 5, though in the classic puzzle \(n\) is supposed to be 64. The discs are stacked on pole A according to their size, the smallest one on top, and the biggest one on the bottom. You now have to move all the discs from pole A to pole C, whereby you have to follow these four rules:
-
you can only move one disc at a time;
-
you can only move discs between the poles;
-
you can only move a disc from a pole if it is on top, and can only move it to the top of another pole;
-
you can never place a disc on top of a disc that is smaller.
Assignment
Write a function hanoi that solves this puzzle for any
value of \(n\). The function must print the solution as a recipe, with lines such as
Move disc 1 from pole A to pole C.
At the end, print the number of moves you needed to make, preferably calculated during the process of generating the recipe.
Tip
To think about a recursive solution, consider the following: Solving the Towers of Hanoi with a biggest disc of size 10 is easy if you know how to solve it for size 9. Namely, you use your size-9 procedure to move the top 9 discs to the middle pole, then move the disc of size 10 to the target pole, and finally use the size-9 procedure to move the 9 discs from the middle pole to the target pole. But how do you solve the problem with the biggest disc being size 9? Well, that is simple if you know how to solve it for size 8… You can imagine where this is going. You are reducing the complexity of the problem step by step, until you are at “solving the problem for size 2 is simple if you can solve it for size 1.” Solving it for size 1 is trivial: you just move the disc to where it must go. Basically, this comes down to a recursive definition of the solution method:
To solve it for size \(n\) where you move from pole X to pole Y with Z as temporary pole, you first solve it for size \(n - 1\) where you move from pole X to pole Z with pole Y as temporary pole, then move the disc of size \(n\) from pole X to pole Y, and finally solve the problem for size \(n - 1\) where you move from pole Z to pole Y with pole X as temporary pole.
Example
>>> hanoi(4)
Disc 1 from A to B
Disc 2 from A to C
Disc 1 from B to C
Disc 3 from A to B
Disc 1 from C to A
Disc 2 from C to B
Disc 1 from A to B
Disc 4 from A to C
Disc 1 from B to C
Disc 2 from B to A
Disc 1 from C to A
Disc 3 from B to C
Disc 1 from A to B
Disc 2 from A to C
Disc 1 from B to C
15 moves needed