Een rechthoekige ruimte is onderverdeeld in vierkantjes van gelijke grootte. De ruimte beslaat $$M$$ vierkantjes in de $$x$$-richting en $$N$$ vierkantjes in de $$y$$-richting. De ruimte kan dus voorgesteld worden door een $$M \times N$$ tabel ($$M$$ rijen en $$N$$ kolommen). Op elk vierkantje kan al dan niet een geldstuk liggen. De $$M\times N$$ tabel $$\verb!r!$$ stelt deze ruimte voor, waarbij het element $$\verb!r[i][j]!$$ aangeeft of op locatie $$(i,j)$$ al dan niet een geldstuk ligt. Elk element van $$\verb!r!$$ is dus True of False.
We beschikken over een doos, met afmetingen $$m \times n$$ (gemeten in vierkantjes, let op: je mag de doos NIET draaien). Bedoeling is om de doos zo te plaatsen in de ruimte zodat ze zoveel mogelijk geldstukken bevat.
Schrijf een methode $$\verb!schat()!$$, met als argumenten

• een NumPy-tabel ($$M$$ rijen en $$N$$ kolommen) van met Boolese waarden, met betekenis zoals hierboven beschreven (minsten 1 rij en minstens 1 kolom)
• de afmetingen van de doos (2 gehele getallen, $$\verb!m!$$ en $$\verb!n!$$), waarbij gegeven is dat $$0 \lt m \lt M$$ en $$ 0 \lt n \lt N$$.

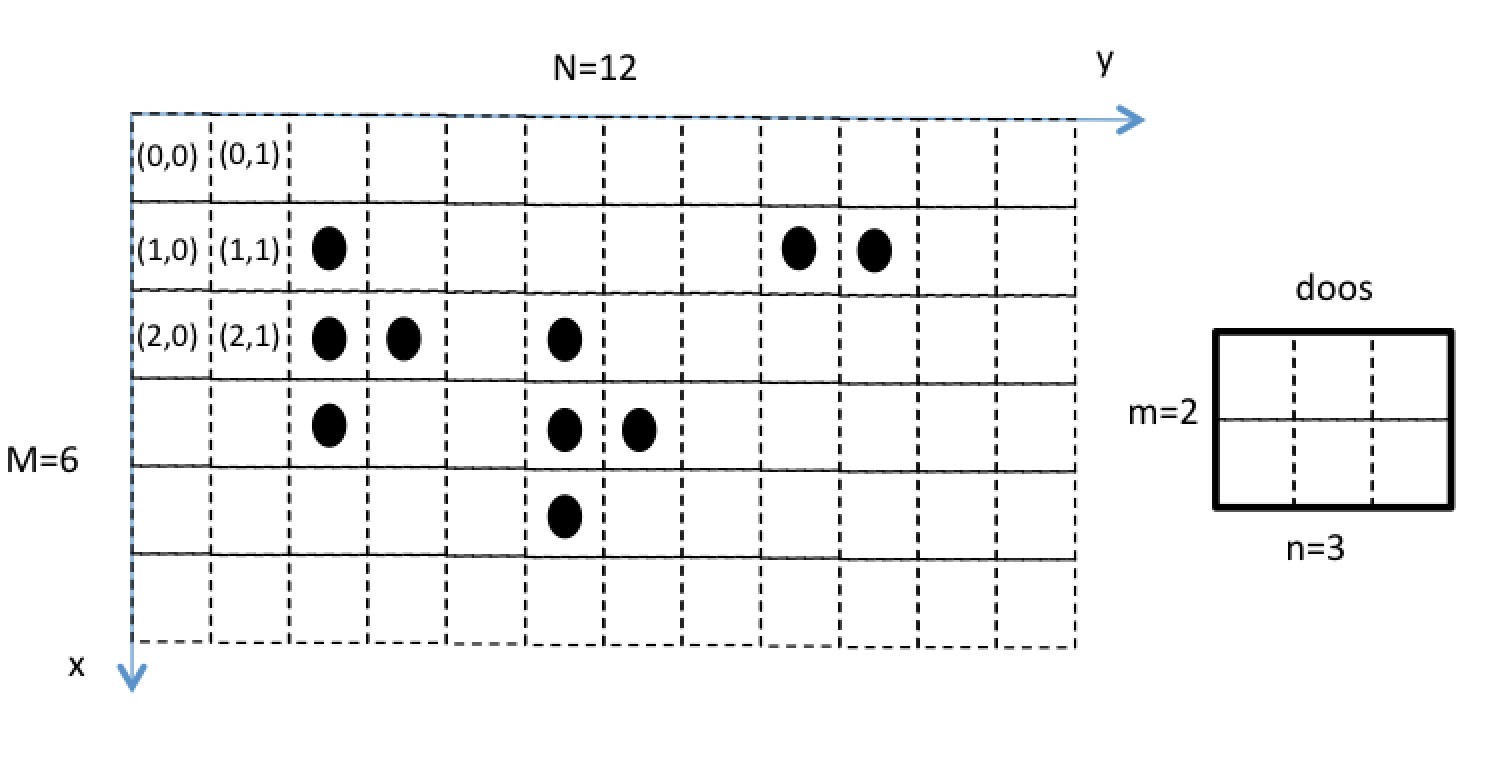
Het resultaat is een tuple, die de optimale positie van de linkerbovenhoek van de doos voorstellen. Dit tuple bestaat dus uit een $$x$$- en $$y$$-coördinaat. Indien meerdere oplossingen mogelijk zijn, kies je de oplossing met kleinste $$x$$-coördinaat. Indien ook nu nog meerdere oplossingen mogelijk blijken, kies je de oplossing met kleinste $$y$$-coördinaat.

Argumenten

Een NumPy-rij in 2 dimensies, $$M>0$$ rijen en $$N>0$$ kolommen, gevolgd door de afmetingen van de doos ($$m$$ en $$n$$).

Resultaat

Een tuple met optimale $$x$$- en $$y$$-coördinaat voor de linkerbovenhoek van de doos.

Voorbeeld

r = np.array(
[[False, False, True, True, False], 
[True, False, False, False, False], 
[True, True, False, False, False],
[False, False, False, False, False], 
[False, True, False, True, True], 
[False, True, False, True, True]]        
) 
schat(r, 2, 2) = (4, 3)
schat(r, 1, 2) = (0, 2)
schat(r, 2, 1) = (1, 0)