In order to fit a logistic regression GAM, we once again use the I() function in constructing the binary response
variable, and set family=binomial.
gam.lr <- gam(I(wage > 250) ~ year + s(age, df = 5) + education, family = binomial, data = Wage)
par(mfrow = c(1, 3))
plot(gam.lr, se = T, col = "green")
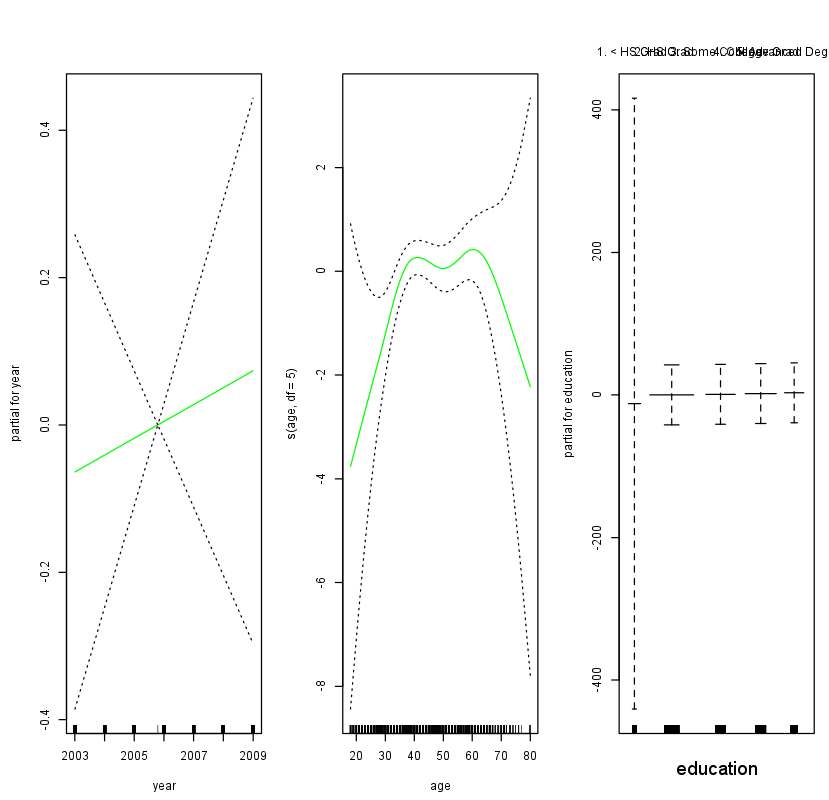
It is easy to see that there are no high earners in the <HS category:
table(education, I(wage > 250))
education FALSE TRUE
1. < HS Grad 268 0
2. HS Grad 966 5
3. Some College 643 7
4. College Grad 663 22
5. Advanced Degree 381 45
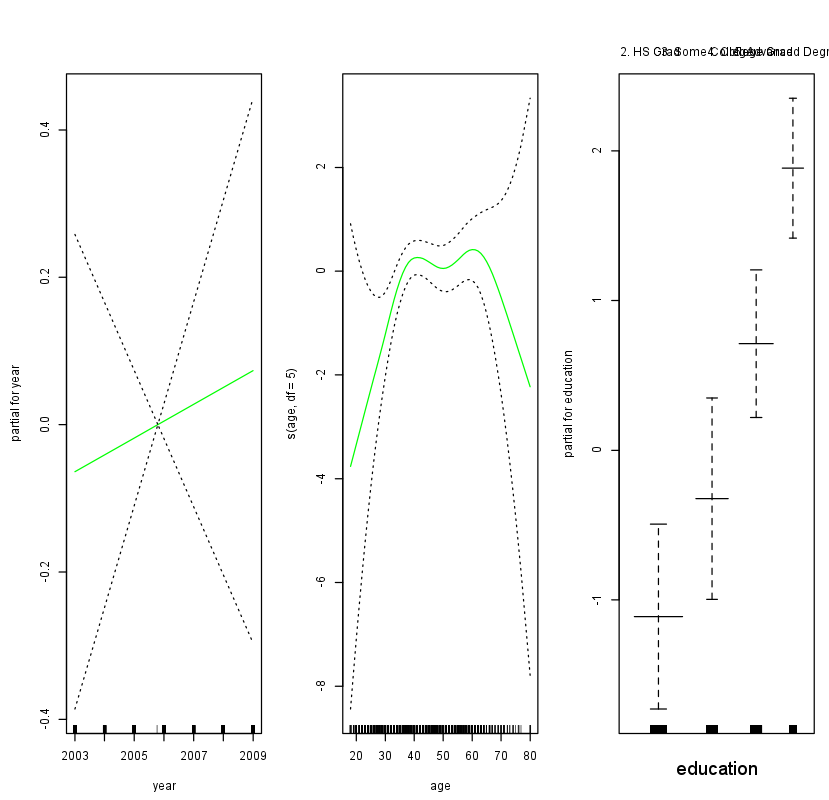
Hence, we fit a logistic regression GAM using all but this category. This provides more sensible results.
gam.lr.s <- gam(I(wage > 250) ~ year + s(age, df = 5) + education, family = binomial, data = Wage,
subset = (education != "1. < HS Grad"))
plot(gam.lr.s, se = T, col = "green")
Questions
- Create a GAM that predicts whether a neighbourhood has a median housing price larger than $ 30,000.
Use the Boston dataset with
medvas dependent variable and a smoothing spline ofdiswith 4 degrees of freedom as independent variable. Also includelstatas independent variable. Keep in mind that the median valuemedvis displayed in $1000s. Store the result ingam1. - Calculate predictions for
medvon the training set. Think about thetypeargument in thepredict()function. Store the results in the variablepreds.
Assume that:
- The MASS library has been loaded
- The Boston dataset has been loaded and attached