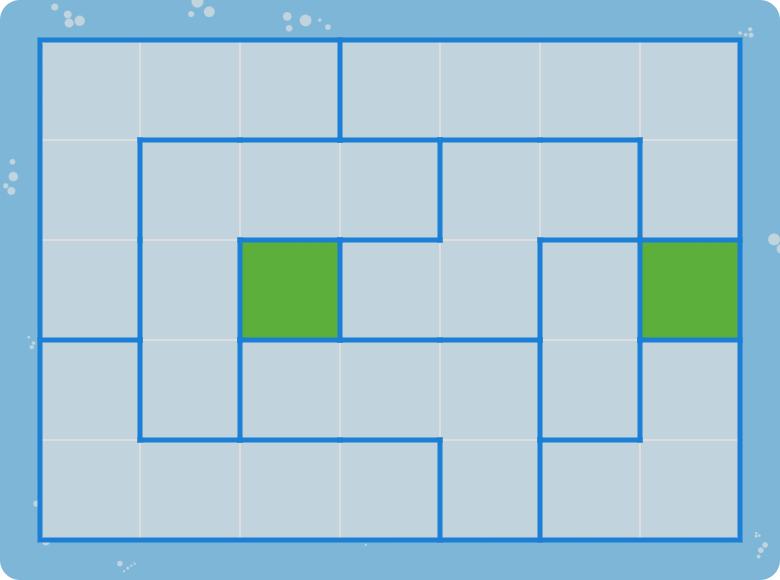
A bubbles and boulders puzzle consists of $$m \times n$$ squares, arranged in a rectangular grid with $$m$$ rows and $$n$$ columns. The grid is split into connected regions of squares that are enclosed by thick blue lines. Green colored squares do not belong to any region. This is an example of such a puzzle whose $$4 \times 4$$ grid is split into four regions.

The goal is to put one bubble and one boulder in every region of the grid, taking into account a couple of rules. Only one bubble or boulder goes into a single square. If there's nothing in their way, boulders sink to the bottom row of the grid and bubbles float to the top row of the grid.
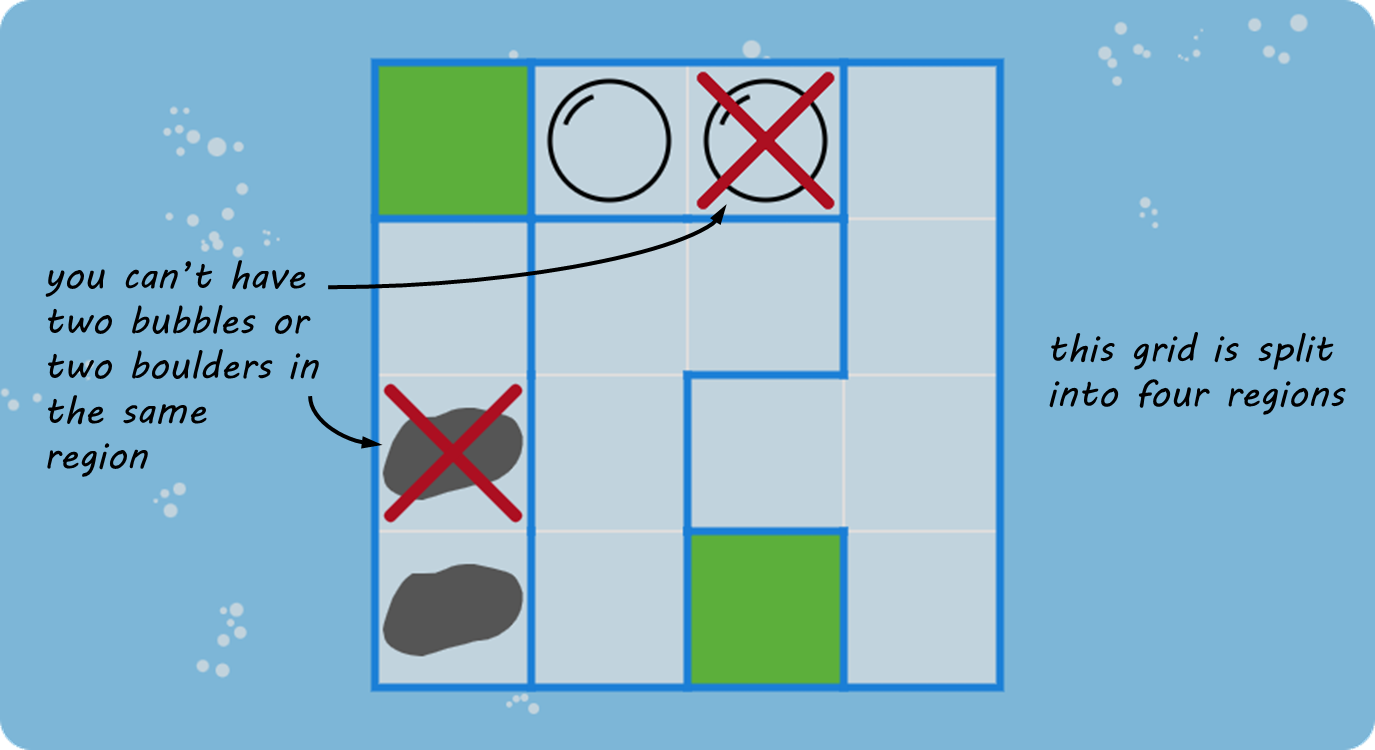
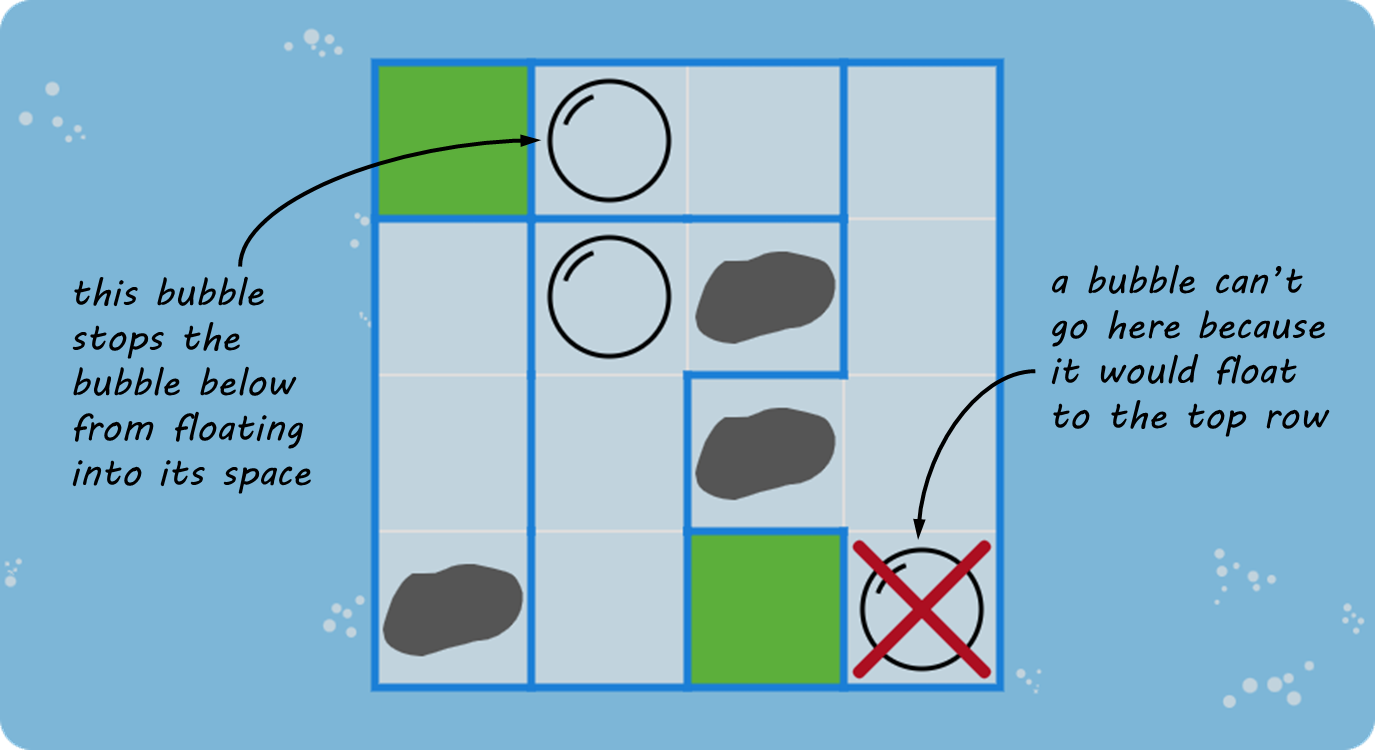
Boulders can sit above green squares, and also above other boulders. But they can't sit above bubbles or empty squares.
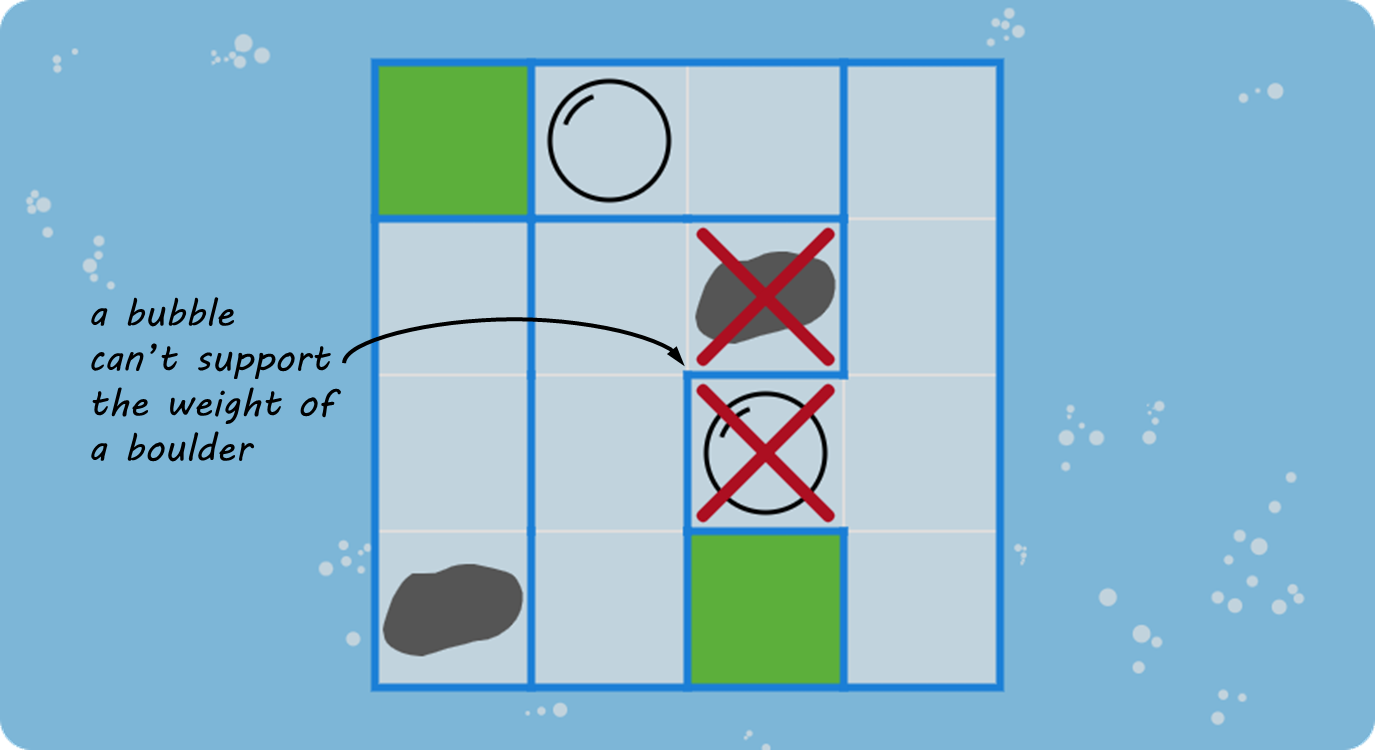
Bubbles can float below green squares, and also below other bubbles. But they can't float below empty squares.
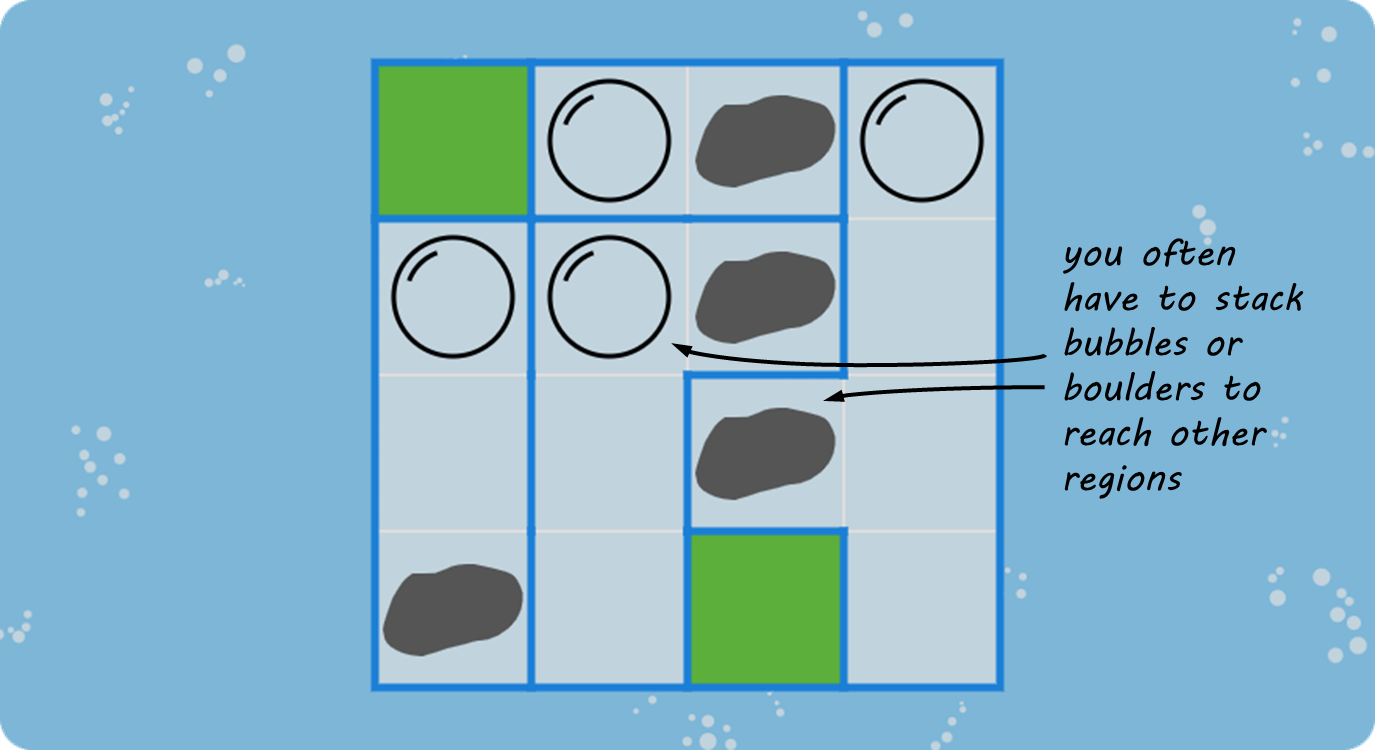
This is the fully solved puzzle, with one bubble and one boulder in each region.
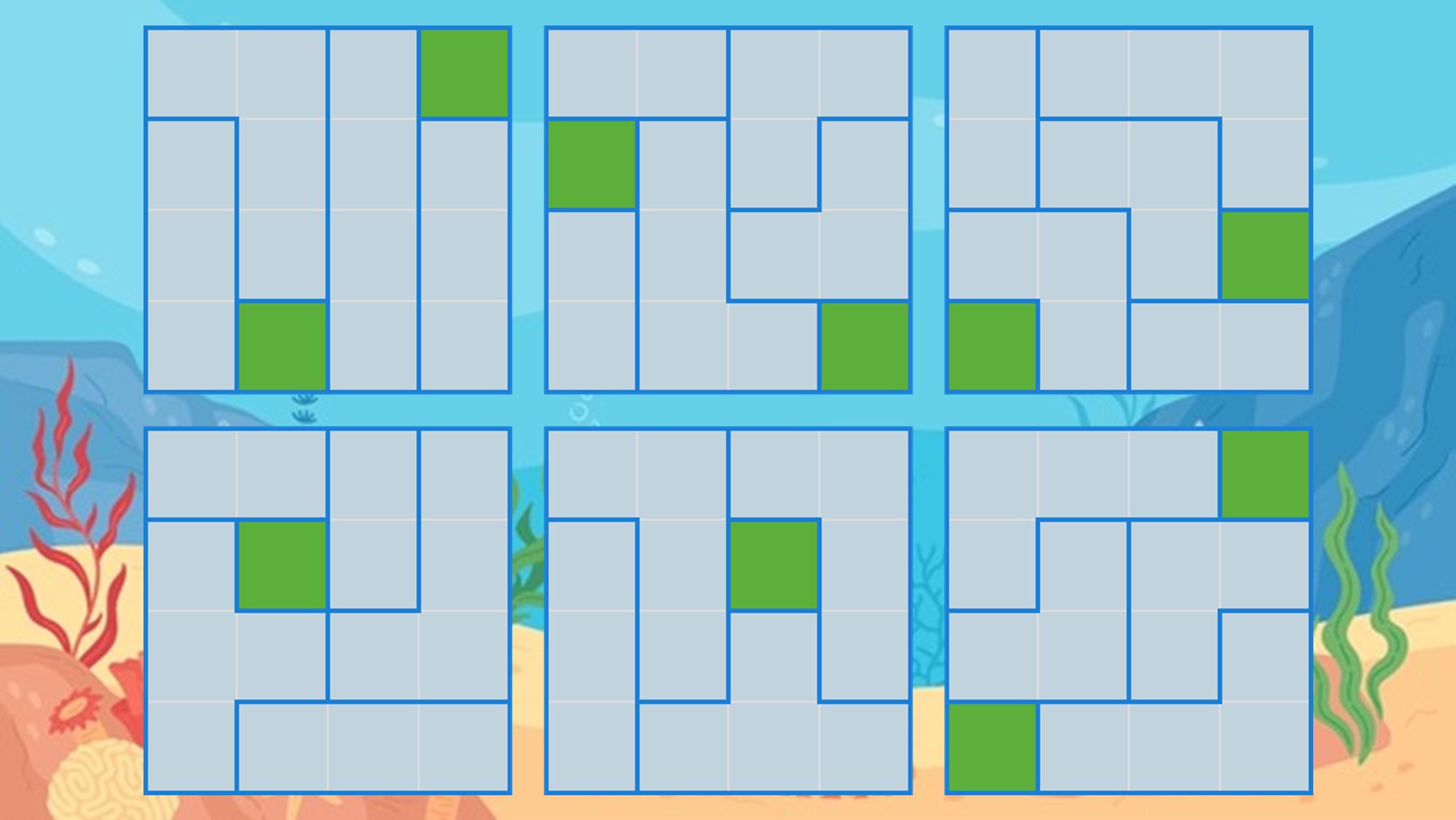
This kind of puzzle is pretty simple once you get the hang of it. But it's best to use a pencil so you can erase any mistakes. Here are some more puzzles to practice. Click here to see the solutions.
Pro tip
When stacking boulders and bubbles, remember that boulders stack from the bottom row up, and bubbles stack from the top row down.
Assignment
A bubbles and boulders puzzle is described in a text file consisting of $$m$$ lines that each describe one row of the $$m \times n$$ grid (from top to bottom). Each line contains $$n$$ characters describing the squares on the corresponding row of the grid (from left to right). All squares belonging to the same region are denoted by the same uppercase letter. Green squares that do not belong to any region are denoted by hashes (#). For example, here's the content of the file describing the puzzle from the introduction (puzzle.txt1):
#AAB
CDDB
CDBB
CD#B
The rows of the grid are numbered from top to bottom, and the columns from left to right, starting from zero. As a result, the position of a square in the grid can be represented as a tuple $$(r, k)$$, with $$r$$ (int) the number of the row and $$k$$ (int) the number of the column where the square appears in the grid.
Define a class Puzzle that can be used to represent and solve bubbles and boulders puzzles. When creating a new puzzle (Puzzle), the location (str) of a text file containing the description of the puzzle must be passed. A puzzle $$p$$ (Puzzle) must have at least the following properties:
-
rows: the number of rows (int) in the grid of puzzle $$p$$
-
columns: the number of columns (int) in the grid of puzzle $$p$$
-
regions: a set containing the uppercase letters (str) that denote the regions in the grid of puzzle $$p$$
If a puzzle $$p$$ (Puzzle) is passed to the built-in function str, the function must return a string representation of the grid that indicates where bubbles and boulders have been placed in puzzle $$p$$. This representation takes the same form as the content of the text file describing puzzle $$p$$, but using the following symbols to represent the state of the squares:
-
a hash (#): a green square
-
an uppercase letter O: a square containing a bubble
-
an asterisk (*): a square containing a boulder
-
a dot (.): an empty square (none of the above cases)
Futhermore, a puzzle $$p$$ (Puzzle) must support at least the following methods:
-
A method squares that takes an uppercase letter (str). If the uppercase letter does not denote a region in the grid of puzzle $$p$$, an AssertionError must be raised with the message invalid region. Otherwise, the method must return a set containing the positions (tuple) of all squares in the grid of puzzle $$p$$ belonging to the corresponding region.
-
A method bubble that takes an uppercase letter (str). If the uppercase letter does not denote a region in the grid of puzzle $$p$$, an AssertionError must be raised with the message invalid region. Otherwise, the method must return the position (tuple) of the square where a bubble was placed in the corresponding region, or the value None if the region does not contain a bubble.
-
A method boulder that takes an uppercase letter (str). If the uppercase letter does not denote a region in the grid of puzzle $$p$$, an AssertionError must be raised with the message invalid region. Otherwise, the method must return the position (tuple) of the square where a boulder was placed in the corresponding region, or the value None if the region does not contain a boulder.
-
A method isempty that takes two integers $$r$$ and $$k$$ (int). The method must return a Boolean value (bool) that indicates if $$(r, k)$$ is the position of an empty square within the grid of puzzle $$p$$: a square within the grid that is not colored green and does not contain a bubble or a boulder.
-
A method put_bubble that takes two integers $$r$$ and $$k$$ (int). If it is impossible to put a bubble at position $$(r, k)$$ in the grid of puzzle $$p$$, an AssertionError must be raised with the message invalid position. This is the case if $$(r, k)$$ is no position of an empty square within the grid of puzzle $$p$$, if a bubble at that position does not float at the top row or below a green square or another bubble, or if the region already contains a bubble at another position. Otherwise, the method must put a bubble at position $$(r, k)$$ in the grid of puzzle $$p$$ and return a reference to $$p$$.
-
A method put_boulder that takes two integers $$r$$ and $$k$$ (int). If it is impossible to put a boulder at position $$(r, k)$$ in the grid of puzzle $$p$$, an AssertionError must be raised with the message invalid position. This is the case if $$(r, k)$$ is no position of an empty square within the grid of puzzle $$p$$, if a boulder at that position does not sit at the bottom row or above a green square or another boulder, or if the region already contains a boulder at another position. Otherwise, the method must put a boulder at position $$(r, k)$$ in the grid of puzzle $$p$$ and return a reference to $$p$$.
-
A method issolved that takes no arguments. The method must return a Boolean value (bool) that indicates whether puzzle $$p$$ was solved. Since the previous two methods guarantee that bubbles and boulders can only be placed in valid positions, this method therefore only needs to check whether a bubble and a boulder were placed in each region of the puzzle $$p$$ grid.
Example
In this interactive session we assume the text file puzzle.txt2 is located in the current directory.
>>> puzzle = Puzzle('puzzle.txt3')
>>> puzzle.rows
4
>>> puzzle.columns
4
>>> puzzle.regions
{'A', 'B', 'C', 'D'}
>>> puzzle.squares('A')
{(0, 1), (0, 2)}
>>> puzzle.squares('B')
{(0, 3), (1, 3), (2, 2), (2, 3), (3, 3)}
>>> puzzle.squares('C')
{(1, 0), (2, 0), (3, 0)}
>>> puzzle.squares('D')
{(1, 1), (1, 2), (2, 1), (3, 1)}
>>> puzzle.squares('E')
Traceback (most recent call last):
AssertionError: invalid region
>>> puzzle.bubble('A')
>>> puzzle.boulder('B')
>>> puzzle.bubble('E')
Traceback (most recent call last):
AssertionError: invalid region
>>> print(puzzle)
#...
....
....
..#.
>>> puzzle.issolved()
False
>>> puzzle.isempty(0, 1)
True
>>> print(puzzle.put_bubble(0, 1))
#O..
....
....
..#.
>>> puzzle.bubble('A')
(0, 1)
>>> puzzle.boulder('A')
>>> puzzle.isempty(0, 1)
False
>>> puzzle.isempty(0, 2)
True
>>> puzzle.put_bubble(0, 2) # second bubble in region A
Traceback (most recent call last):
AssertionError: invalid position
>>> puzzle.isempty(2, 0)
True
>>> puzzle.put_boulder(2, 0) # boulder floats above empty square
Traceback (most recent call last):
AssertionError: invalid position
>>> puzzle.isempty(3, 0)
True
>>> print(puzzle.put_boulder(3, 0))
#O..
....
....
*.#.
>>> puzzle.bubble('C')
>>> puzzle.boulder('C')
(3, 0)
>>> puzzle.issolved()
False
>>> puzzle.put_boulder(2, 0) # second boulder in region C
Traceback (most recent call last):
AssertionError: invalid position
>>> puzzle.put_bubble(3, 2) # bubble in green square
Traceback (most recent call last):
AssertionError: invalid position
>>> puzzle.put_bubble(2, 2) # bubble floats below empty square
Traceback (most recent call last):
AssertionError: invalid position
>>> puzzle.put_boulder(1, 2) # boulder floats above empty square
Traceback (most recent call last):
AssertionError: invalid position
>>> print(puzzle.put_bubble(1, 1).put_boulder(2, 2).put_boulder(1, 2))
#O..
.O*.
..*.
*.#.
>>> puzzle.issolved()
False
>>> puzzle.put_bubble(3, 3) # bubble floats below empty square
Traceback (most recent call last):
AssertionError: invalid position
>>> print(puzzle.put_bubble(1, 0).put_boulder(0, 2).put_bubble(0, 3))
#O*O
OO*.
..*.
*.#.
>>> puzzle.issolved()
True
Epilogue
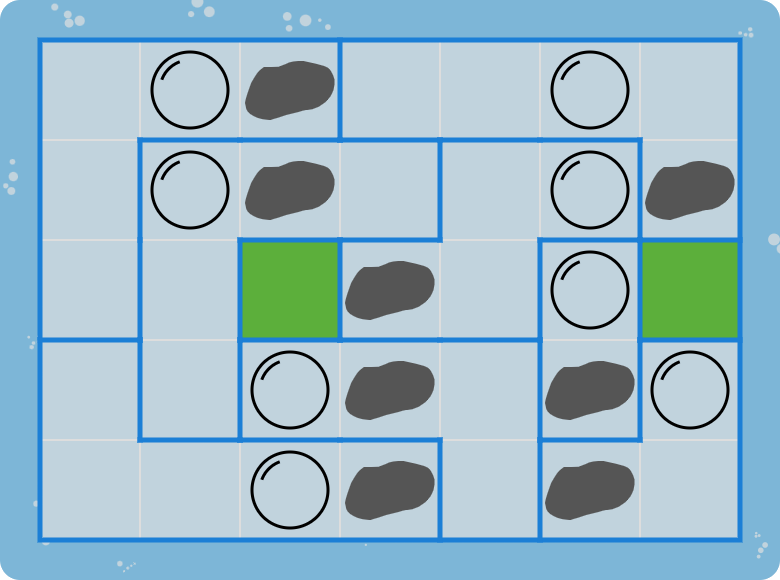
So far, we only gave examples of smaller puzzles with a square $$4 \times 4$$ grid. Here's a somewhat larger puzzle with a rectangular $$5 \times 7$$ grid that is also used to test the solutions you submit for this assignment. Click here to see the unique solution of this puzzle.