It is claimed that in the case of data that is just barely linearly separable, a support vector classifier with a small value of “cost” that misclassifies a couple of training observations may perform better on test data than one with a huge value of “cost” that does not misclassify any training observations. You will now investigate that claim.

First we generate two-class data with \(p = 2\) in such a way that the classes are just barely linearly separable. We randomly generate 1000 points and scatter them across line \(x = y\) with wide margin. We also create noisy points along the line \(5x − 4y − 50 = 0\). These points make the classes barely separable and also shift the maximum margin classifier.

set.seed(1)
x.one <- runif(500, 0, 90)
y.one <- runif(500, x.one + 10, 100)
x.one.noise <- runif(50, 20, 80)
y.one.noise <- 5/4 * (x.one.noise - 10) + 0.1

x.zero <- runif(500, 10, 100)
y.zero <- runif(500, 0, x.zero - 10)
x.zero.noise <- runif(50, 20, 80)
y.zero.noise <- 5/4 * (x.zero.noise - 10) - 0.1

class.one <- seq(1, 550)
x <- c(x.one, x.one.noise, x.zero, x.zero.noise)
y <- c(y.one, y.one.noise, y.zero, y.zero.noise)

plot(x[class.one], y[class.one], col = "blue", pch = "+", ylim = c(0, 100))
points(x[-class.one], y[-class.one], col = "red", pch = 4)

z <- rep(0, 1100)
z[class.one] <- 1
data <- data.frame(x = x, y = y, z = as.factor(z))

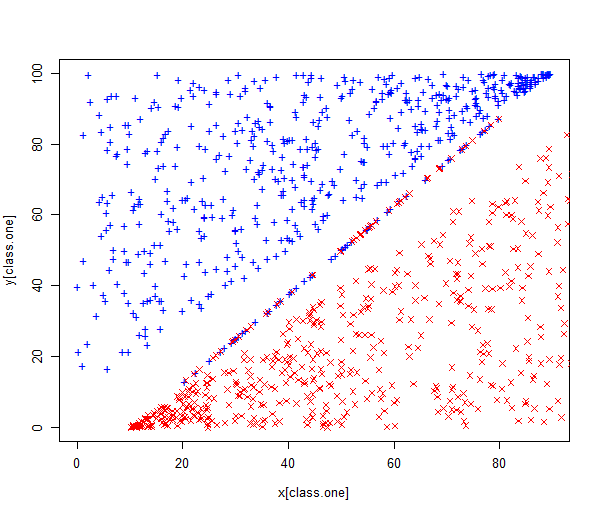
The data set is stored in the dataframe data, has one dependent variable z and two independent variables x and y. We will use this data set as the training data for our classifiers.

Questions

1. Compute the cross-validation error rates for support vector classifiers with a range of cost values using the tune() function. Use the following range: c(0.01, 0.1, 1, 5, 10, 100, 1000, 10000). Store the output of the tune() function in tune.out and set.seed(2) before running the cross-validation.

2. How many training errors are misclassified for each value of cost considered, and how does this relate to the cross-validation errors obtained? Create a dataframe train.misclass with two columns, the first column is named “cost” and contains all the values of cost tested in the cross-validation (this is stored in tune.out$performance$cost), the second column is named “n_misclassified” and contains the number of misclassified observations (you can find the mean error rate of each cross-validation in tune.out$performance$error).

3. Now we generate an appropriate test data set.

   x.test <- runif(1000, 0, 100)
   class.one <- sample(1000, 500)
   y.test <- rep(NA, 1000)
   # Set y > x for class.one
   for (i in class.one) {
       y.test[i] <- runif(1, x.test[i], 100)
   }
   # set y < x for class.zero
   for (i in setdiff(1:1000, class.one)) {
       y.test[i] <- runif(1, 0, x.test[i])
   }
   plot(x.test[class.one], y.test[class.one], col = "blue", pch = "+")
   points(x.test[-class.one], y.test[-class.one], col = "red", pch = 4)
   set.seed(3)
   z.test <- rep(0, 1000)
   z.test[class.one] <- 1
   data.test <- data.frame(x = x.test, y = y.test, z = as.factor(z.test))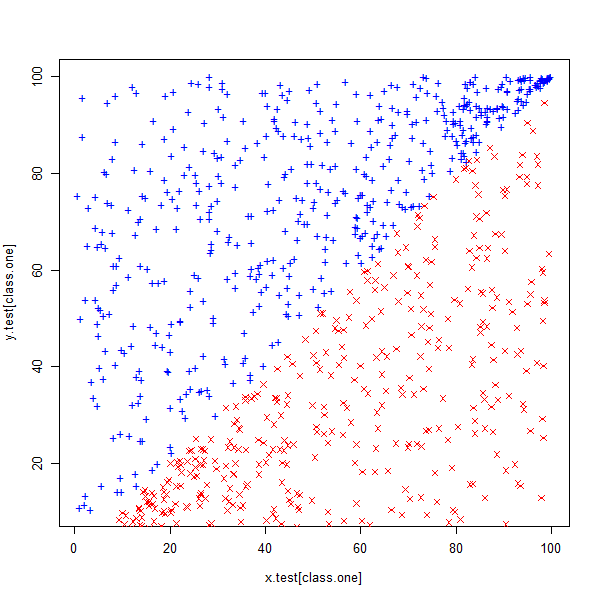
   

   

   We also define the range of values we want to test for cost.

   costs <- c(0.01, 0.1, 1, 5, 10, 100, 1000, 10000)
   

   Compute the test errors corresponding to each of the values of cost considered.

   1. Create a vector test.err with the same length as costs
   2. Write a for loop where \(i\) goes from 1 to length(costs) and each iteration:
      1. Trains a SVM with a linear kernel on the training data with a cost value according to that iteration.
      2. The test error is stored in at the \(i\)th place in test.err.
   3. Create a dataframe test.misclass with two columns, the first column is named “cost” and contains all the values of cost used for training, the second column is named “n_misclassified” and contains the number of misclassified test observations according to each cost value.
4. MC1: Which of these statements is false (only one answer)?
   1. The optimal cost value found for training observations is smaller than the optimal cost value found for the test observations.
   2. Comparing the results between 2 & 3, the SVM with a linear kernel is prone to overfitting.
   3. A large cost tries to correctly classify noisy-points and hence overfits the train data
   4. A small cost makes a few errors on the noisy-points and performs better on test data

---

Assume that:

• The e1071 library has been loaded