Curling has been an official sport in the Winter Olympic Games since the 1998 Winter Olympics in Nagano, Japan. In the run-up to this year's Winter Olympics it's about time we get to know this sport — which somewhat resembles bowls on ice — a little better.

Two four-player teams — team red and team yellow — take turns sliding heavy, polished granite stones across a curling sheet towards the house: a circular target area marked on the ice which is segmented into four concentric rings. Each team has eight stones. The purpose is to accumulate the highest score for a game. A game usually consists of eight to ten ends, which are completed when both teams have thrown all of their stones.
Points are scored for the stones resting closest to dolly (the center of the house) at the conclusion of each end. The team with the stone closest to the dolly wins that end. The winning team is then awarded one point for each of its stones lying closer to the dolly than the opponent's closest stone. Only stones that are in the house are considered in scoring. A stone is in the house if it overlaps — even if it's only a tiny fraction — with the circle formed by the outer edge of the outer ring of the house. Below you can see some example scores at the conclusion of an end.
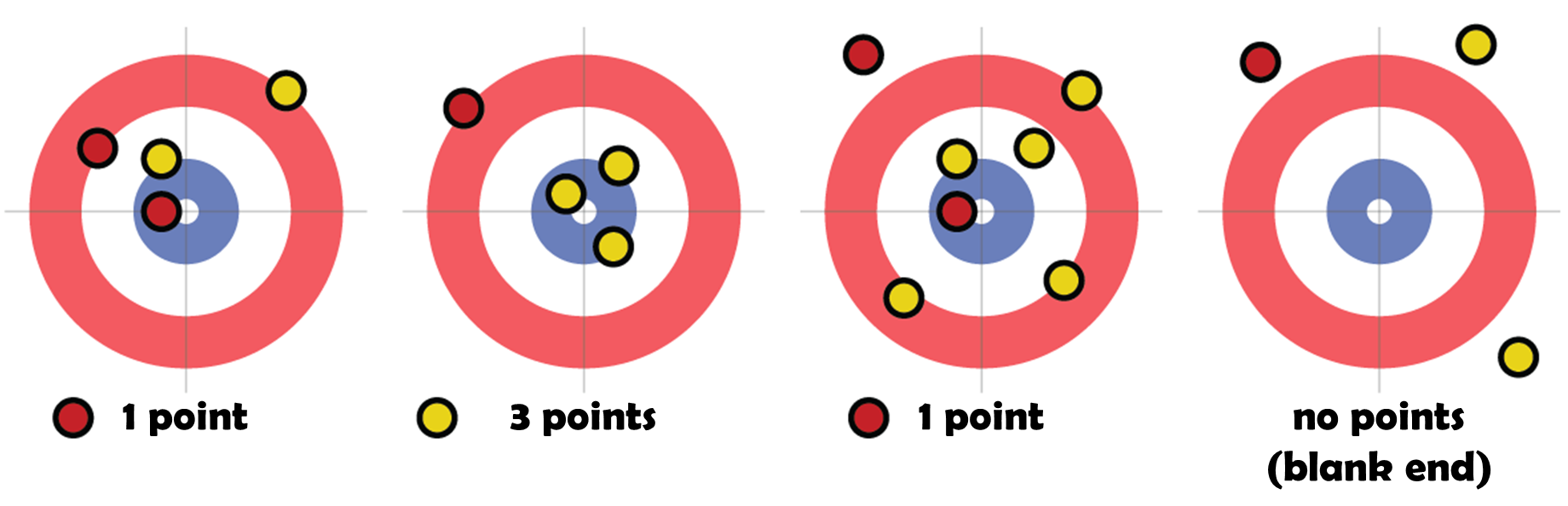
The colors of the rings have no special meaning. They are only used to make it easier to estimate how the stones are in position to the dolly and to each other. After all, curling is a game of fractions and it may not be obvious to the eye which of two stones is closer to the dolly or if a stone is actually in the house or not. There are specialized devices to make these determinations, but these cannot be brought out until after an end is completed. Therefore, a team may make strategic decisions during an end based on assumptions of stone positions that turn out to be incorrect. In addition, the specialized measuring devices are so accurate that an end can never result in a tie, except if there are no stones in the house.
Assignment
Determine the score of the two teams, given the positions of the stones after an end in a game of curling has completed. The positions of the stones are represented as a sequence (a list or a tuple) containing descriptions of $$r + y$$ stones, where $$r$$ indicates the number of red stones ($$0 \leq r \leq 8$$) and $$y$$ the number of yellow stones ($$0 \leq y \leq 8$$).
Each stone is described as a tuples $$(x, y, t)$$, with $$(x, y)$$ the coordinates of the center of the stone in a coordinate system that has its origin in the dolly ($$x, y \in \mathbb{R}$$) and $$t$$ a string that indicates the color of the stone (R for red and Y for yellow).
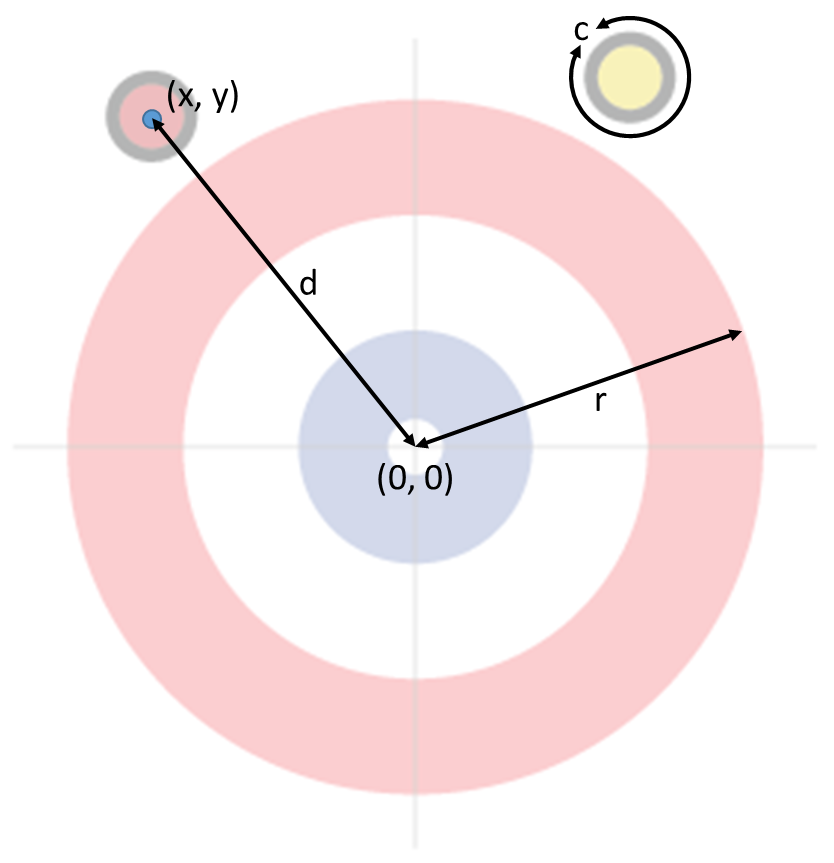
Curling is all about circles: to determine the score you have to know if a circular stone is in the circular house and you must also determine the distance from the center of the circular stones to the dolly (the center of the circular house). We help you out in listing some measures used in curling and also remind you about some circle measures (see figure above as a reference):
-
the house is a circle (outer edge of outer ring) with a radius $$r$$ of 6 feet
-
the stones are circles with a circumference $$c$$ of 36 inches
-
relationship between circumference $$c$$ of a circle and its radius $$r$$: $$c = 2\pi r$$
-
distance $$d$$ between the dolly and a stone with center in position $$(x, y)$$ is $$\sqrt{x^2 + y^2}$$
-
1 feet = 12 inch
-
1 inch = 0.0254 meter
Your task:
-
Write a function inHouse that takes the $$x$$ and the $$y$$ coordinate of the center of a stone in a coordinate system that has its origin in the dolly ($$x, y \in \mathbb{R}$$). The function also has an optional third parameter inch that may take a Boolean value (default value: True). The parameter inch indicates if the coordinates of the stone are expressed in inch (True) or in meter (False). The function must return a Boolean value that indicates if the stone is in the house.
-
Write a function validPositions that takes the positions of the stones after an end in a game of curling has completed. The function also has an optional second parameter inch that has the same meaning as with the function inHouse. The function validStones must return a Boolean value that indicates if the given positions of the stones are valid. This is the case if there are no more than eight stones of each color and if there are no overlapping stones (which is physically impossible).
-
Write a function score that takes the positions of the stones after an end in a game of curling has completed. The function also has an optional second parameter inch that has the same meaning as with the function inHouse. The function score must return the score at the conclusion of the end as a tuple $$(s_r, s_y)$$, with $$s_r$$ the score of team red and $$s_y$$ the score of team yellow. If the given positions of the stones are invalid (as defined by the function validPositions), an AssertionError must be raised with the message invalid stone positions.
Example
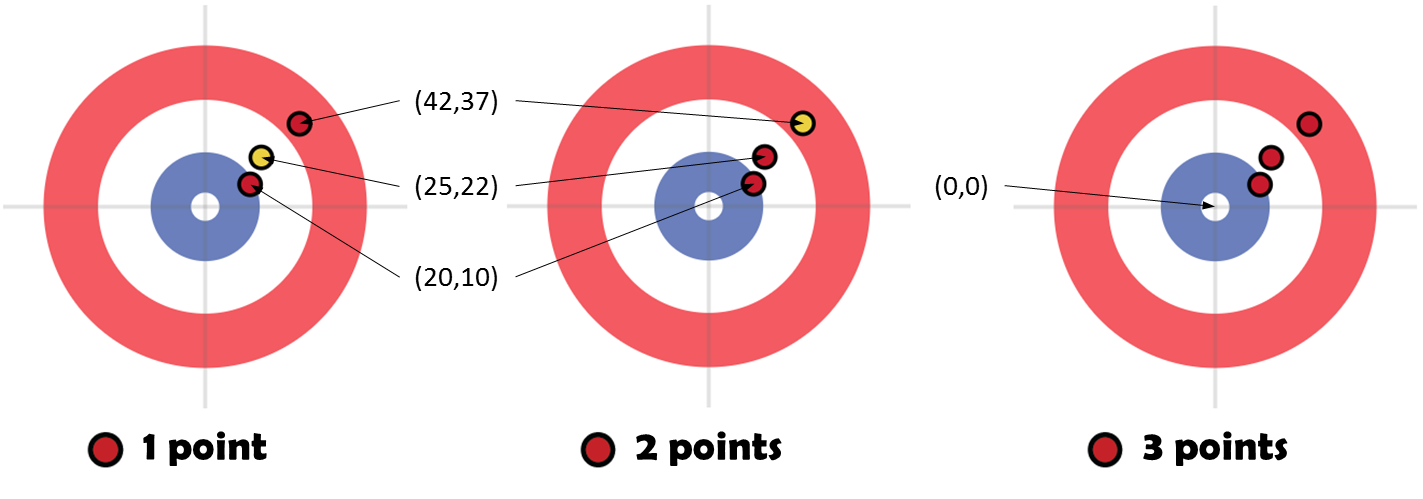
>>> inHouse(70.0, 0.0) True >>> inHouse(70.0, 0.0, inch=False) False >>> inHouse(78.0, 0.0) False >>> validPositions([(20.0, 10.0, 'R'), (25.0, 22.0, 'Y'), (42.0, 37.0, 'R')]) True >>> validPositions([(20.0, 10.0, 'R'), (25.0, 22.0, 'R'), (42.0, 37.0, 'Y')]) True >>> validPositions([(20.0, 10.0, 'R'), (25.0, 22.0, 'R'), (42.0, 37.0, 'R')]) True >>> score([(20.0, 10.0, 'R'), (25.0, 22.0, 'Y'), (42.0, 37.0, 'R')]) (1, 0) >>> score([(20.0, 10.0, 'R'), (25.0, 22.0, 'R'), (42.0, 37.0, 'Y')]) (2, 0) >>> score([(20.0, 10.0, 'R'), (25.0, 22.0, 'R'), (42.0, 37.0, 'R')]) (3, 0) >>> score([(0.508, 0.254, 'R'), (0.635, 0.5588, 'Y'), (1.0668, 0.9398, 'R')], False) (1, 0) >>> score([(0.508, 0.254, 'R'), (0.635, 0.5588, 'R'), (1.0668, 0.9398, 'Y')], inch=False) (2, 0) >>> score([(0.508, 0.254, 'R'), (0.635, 0.5588, 'R'), (1.0668, 0.9398, 'R')], False) (3, 0)
All examples for the function score take a sequence of stones at the same positions (the first three example express them in inch, the last three examples in meter), but with different colors. Here's a graphical representation of the positions and colors of these stones, with coordinates expressed in inch.