I hand you an ordinary deck of 52 cards. You inspect and shuffle it, then choose five cards from the deck and hand them to my assistant. She looks at them and passes four of them to me. I name the fifth card.

At first this appears impossible. The hidden card is one of 48 possibilities, and by passing me four cards in some order my assistant can have sent me only one of $$4! = 24$$ messages. How am I able to name the card?
Part of the secret is that my assistant gets to choose which card to withhold. The group of five cards that you've chosen must contain two cards of the same suit (a consequence of the pigeonhole principle). My assistant chooses one of these to be the hidden card and passes me the other one. Now I know the suit of the hidden card, and there are 12 possibilities as to its rank. But my assistant can pass me only three more cards, with $$3! = 6$$ possible messages, so the task still appears impossible.
The rest of the secret lies in my assistant's choice as to which of the two same-suit cards to give me. Think of the 13 card ranks arranged in a circle (with ace = 1, jack = 11, queen = 12 and king = 13). Given two ranks, it's always possible to get from one to the other in at most 6 steps by traveling "the short way" around the circle.
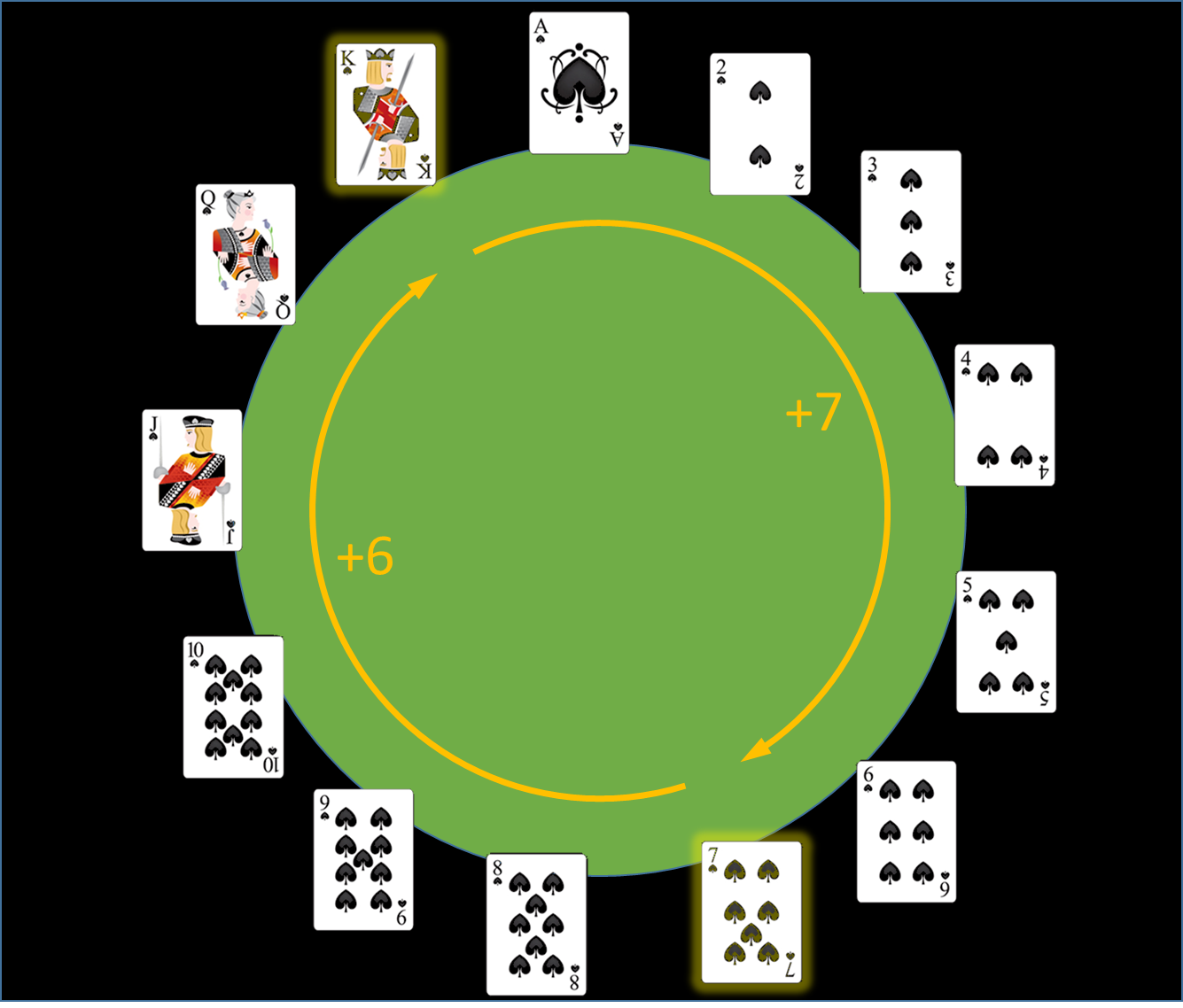
So me and my assistant agree on a convention beforehand: we'll imagine that the ranks increase in value (ace, 2, …, 10, jack, queen, king), and the suits as in bridge order: clubs, diamonds, hearts, spades. This puts the whole deck into a specified order, and my assistant can pass me the three remaining cards in one of six ways:
\[\begin{eqnarray} \{\textrm{low}, \textrm{middle}, \textrm{high}\} &=& 1 \\ \{\textrm{low}, \textrm{high}, \textrm{middle}\} &=& 2 \\ \{\textrm{middle}, \textrm{low}, \textrm{high}\} &=& 3 \\ \{\textrm{middle}, \textrm{high}, \textrm{low}\} &=& 4 \\ \{\textrm{high}, \textrm{low}, \textrm{middle}\} &=& 5 \\ \{\textrm{high}, \textrm{middle}, \textrm{low}\} &=& 6 \\ \end{eqnarray}\]
So if my assistant knows that I'll always travel clockwise around the imaginary circle, she can choose the first card to establish the suit of the hidden card and to specify one point on the circle, and then order the remaining three cards to tell me how many clockwise steps to take from that point to reach the hidden rank.
"If you haven't seen this trick before, the effect really is remarkable. Reading it in print does not do it justice.", writes mathematician Michael Kleber. "I am forever indebted to a graduate student in one audience who blurted out 'No way!' just before I named the hidden card." The trick first appeared in print in Wallace Lee's 1950 book Math Miracles. Lee attributes it to William Fitch Cheney, a San Francisco magician and the holder of the first math Ph.D. ever awarded by MIT.
Assignment
In this assignment we represent the ranks of the cards using the strings
ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, jack, queen, king
and we represent the suits of the cards using the strings
clubs, diamonds, hearts, spades
These sequences also impose a fixed order on a deck of cards, as explained in the introduction.
Define a class Card that can be used to represent the cards in an ordinary deck of 52 cards. Upon initialization of an object of the class Card, the rank and the suit of the card must be given. In case an invalid rank or an invalid suit is given, an AssertionError must be raised with the message invalid card. Make sure that objects of the class Card can be represented as a string as indicated in the example below, and that the six comparison operators (<, >, <=, >=, == and !=) can be used to compare two cards with each other based on the fixed order imposed on a deck of cards.
In addition, you have to implement a function fifthCard that takes a sequence (a list or a tuple) of four different cards (objects of the class Card). These represent the four cards the assistant hands over to the magician. The function must return the card (another object of the class Card) the assistant keeps hidden for the magician.
Example
>>> Card('ace', 'spades') Card(rank='ace', color='spades') >>> print(Card('ace', 'spades')) ace of spades >>> Card('ace', 'pikes') Traceback (most recent call last): AssertionError: invalid card >>> Card('ace', 'spades') < Card('knight', 'hearts') True >>> Card('ace', 'spades') >= Card('knight', 'hearts') False >>> fifthCard([Card('7', 'spades'), Card('queen', 'hearts'), Card('8', 'clubs'), Card('3', 'diamonds')]) Card(rank='king', color='spades')