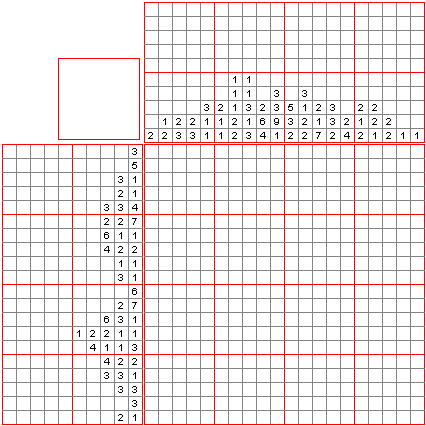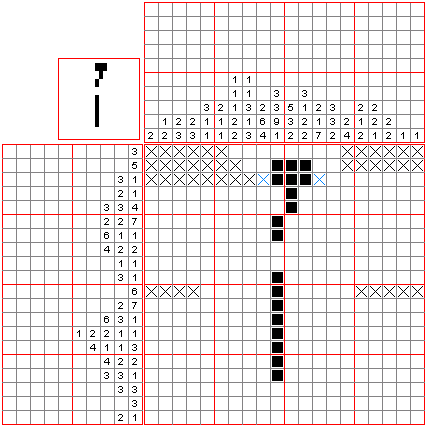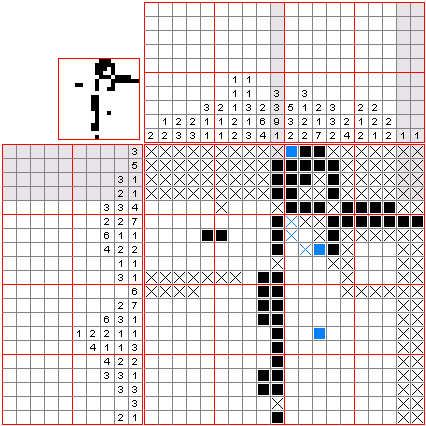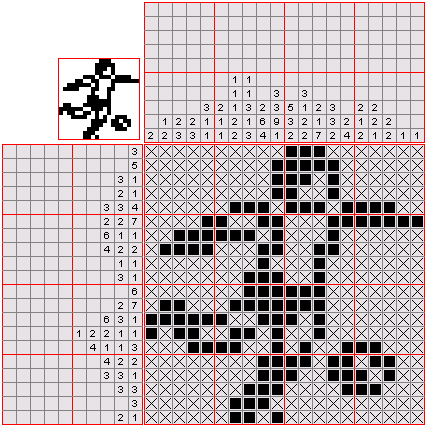
A Nonogram is a Japanese picture puzzle in which a hidden picture can be found. This image can be formed by colouring the boxes of a rectangular lattice black or white, taking into account the set of integers that is specified for each row and each column of the grid. These numbers indicate how many consecutive black squares there should be in that row or column. For example, if the grid indicates the series 4 8 3 , this means that the row or column is made up of sets of four, eight, and three consecutive black boxes, in that order, and that there is at least one white box between each of the consecutive series.

Example of a Nonogram puzzle while it is being solved. Some steps of the process were combined.

Assignment

For this task, you must solve a simplified version of the Nonogram puzzle. As with the original puzzle, the sequences of black boxes in each row are provided. The description for the columns, however, is no longer needed. For each set of consecutive black boxes is now defined by a couple of integers $$(s, l)$$, where $$s$$ and $$l$$ indicate the start position and the length of the series, respectively. The far-left cell of a row is at position zero.

Solution of a simplified version of a Nonogram puzzle where both the starting position and length is specified for each series of consecutive black squares.

Note that the order in which the sequences of consecutive black boxes are given no longer plays a role. A row of a Nonogram puzzle can thus be defined by a series of number pairs that indicate the start position and the length of the series, respectively, of the consecutive black boxes.

Input

The input defines the specifications of a simplified Nonogram puzzle. The first line of the input contains two integers $$h$$ and $$b$$ which indicate the height and the width of the image. The two numbers are separated from each other by a single space. This is followed by $$h$$ lines that each describe another line of the hidden image. This description consists of pairs of integers: each pair consists of two integers, separated by a comma and enclosed in parentheses. The pairs themselves are each separated by a comma. Except between the figures of the same integer, spaces can be everywhere. The first and second number of each pair indicate the starting position and length, respectively, of a succession of black boxes on the line of the image.

Output

Print the hidden image described by the entry. This image is a rectangular $$h \times b$$ grid of which the white boxes are represented by spaces, and black boxes by hashes (#). The total number of spaces and hashes of each line must be equal to $$b$$.

Example

Input:

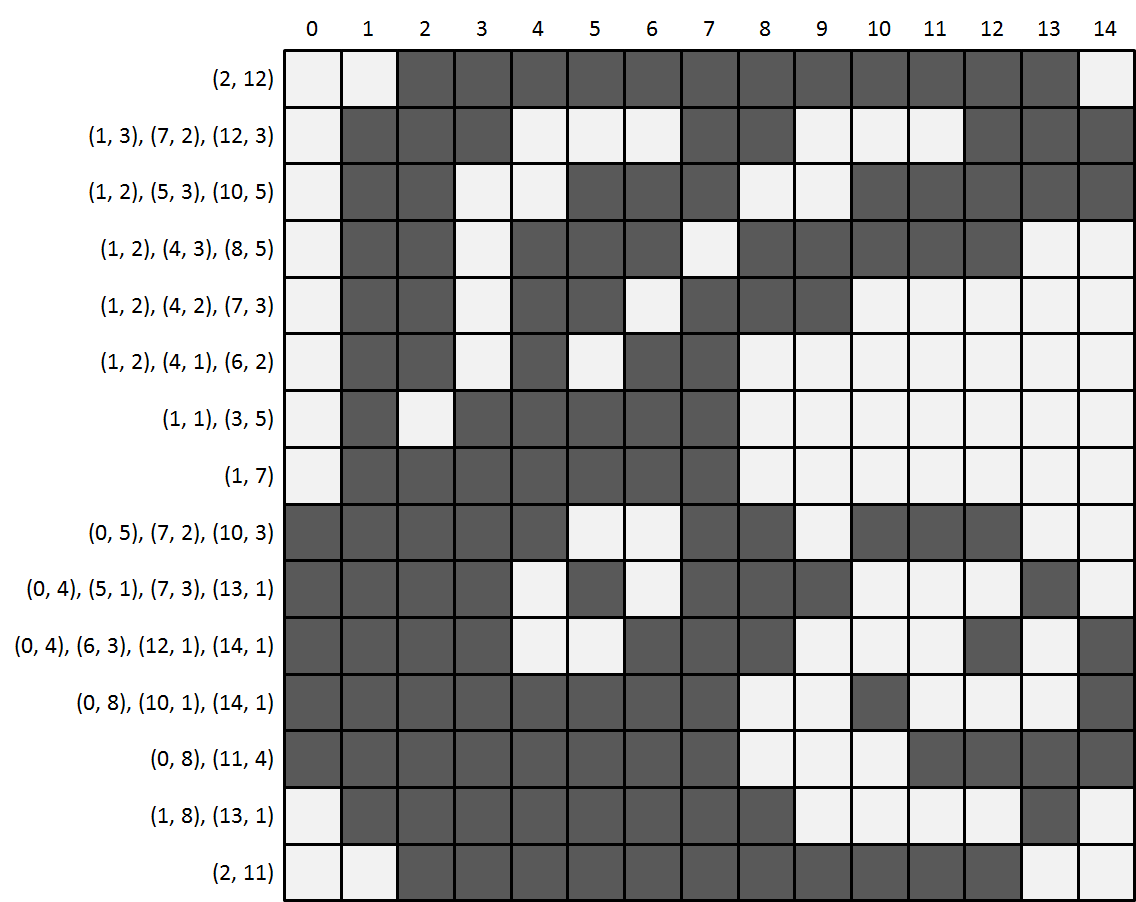
15 15
(2, 12)
(1, 3), (7, 2), (12, 3)
(1, 2), (5, 3), (10, 5)
(1, 2), (4, 3), (8, 5)
(1, 2), (4, 2), (7, 3)
(1, 2), (4, 1), (6, 2)
(1, 1), (3, 5)
(1, 7)
(0, 5), (7, 2), (10, 3)
(0, 4), (5, 1), (7, 3), (13, 1)
(0, 4), (6, 3), (12, 1), (14, 1)
(0, 8), (10, 1), (14, 1)
(0, 8), (11, 4)
(1, 8), (13, 1)
(2, 11)

Output:

  ############ 
 ###   ##   ###
 ##  ###  #####
 ## ### #####  
 ## ## ###     
 ## # ##       
 # #####       
 #######       
#####  ## ###  
#### # ###   # 
####  ###   # #
########  #   #
########   ####
 ########    # 
  ###########