A combination lock is a type of padlock in which a sequence of numbers is used to open and close the lock. The sequence may be entered using a set of independently rotating discs with inscribed numerals. The discs directly interact with the locking mechanism, following the principle outlined using the following illustrations.

Exploded view of the rotating discs. The notches on the discs correspond to the numerals in the correct combination. In this case, the combination is 9-2-4.

The discs are mounted on one side of the lock, which may in turn be attached to the end of a chain or cable. The other side of the lock, or the other end of the cable, has a pin with several protruding teeth.

When the toothed pin is inserted and the discs are rotated to an incorrect combination, the inner faces of the discs block the pin from being extracted.

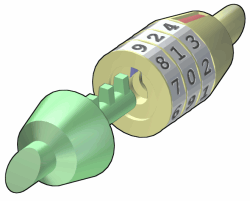
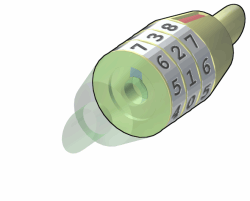
Assignment

Write a class CombinationLock which can be used to initiate objects that represent a combination lock having $$d \in \mathbb{N}_0$$ rotating discs. Each disc is inscribed with the integer series 0, 1, …, $$m$$. There is a single correct combination to which the discs must be set in order to open the lock. The objects of the class CombinationLock must at least support the following methods:

An initialization method that takes a sequence (a list or a tuple) of integers as its argument. These integers indicate the correct combination to open the lock. The number of integers $$d \in \mathbb{N}_0$$ corresponds to the number of discs of the lock. Initially each lock is set to the value zero. In addition, the initialization method has a second optional parameter maxvalue that takes the maximal value $$m \in \mathbb{N}_0$$ with which the discs are inscribed (default value: 9). The lock needs to have at least a single disc, and each integer in the correct combination must be in the interval [0, $$m$$]. If this is not the case, the initialization method must raise an AssertionError with the message invalid combination.
A method __repr__ that must return a string representation of the object in the format CombinationLock(t, maxvalue=m), where t is a tuple that contains the integer sequence that forms the correct combination to open the lock, and m represents the maximal value with which the discs are inscribed.
A method __str__ that must return a string representation of the object. This string representation must contain the integer sequence to which the discs are currently set, separated from each other using dashes.
A method rotate that can be used to rotate one or more discs over a given number of positions. This method takes two arguments: i) the discs that need to rotated, and ii) the number of positions the discs need to be rotated. Disc are always rotated to a larger value, where after the integer $$m$$ the disc is rotated to zero. To indicate which discs need to be rotated, the discs are increasingly indexed from left to right, starting at zero. In case a single disc needs to be rotated, the index of the disc (integer) is passed as the first argument. In case multiple discs need to be rotated, a collection (a list, tuple or set) of disc indices (integers) is passed as the first argument. If the index of a non-existing disc is passed to the method rotate, an AssertionError must be raised with the message invalid disc. In that case, non of the given discs must be rotated.
A method open that returns a Boolean value indicating whether or not the discs are set to the correct combination that opens the lock.

Example

>>> lock = CombinationLock((9, 2, 4))
>>> lock
CombinationLock((9, 2, 4), maxvalue=9)
>>> print(lock)
0-0-0
>>> lock.open()
False
>>> lock.rotate(1, 2)
>>> print(lock)
0-2-0
>>> lock.rotate(2, 5)
>>> print(lock)
0-2-5
>>> lock.open()
False
>>> lock.rotate([2, 0], 9)
>>> print(lock)
9-2-4
>>> lock.open()
True

>>> lock = CombinationLock([14, 13, 2, 7, 6], maxvalue=16)
>>> lock
CombinationLock((14, 13, 2, 7, 6), maxvalue=16)
>>> print(lock)
0-0-0-0-0
>>> lock.rotate([0, 2, 4], 6)
>>> print(lock)
6-0-6-0-6
>>> lock.rotate([1, 3, 5], 13)
Traceback (most recent call last):
AssertionError: invalid disc
>>> print(lock)
6-0-6-0-6
>>> lock.rotate([1, 3, 2], 13)
>>> print(lock)
6-13-2-13-6
>>> lock.rotate([0, 3], 8)
>>> print(lock)
14-13-2-4-6
>>> lock.open()
False
>>> lock.rotate(3, 3)
>>> print(lock)
14-13-2-7-6
>>> lock.open()
True

>>> lock = CombinationLock([1, 2, 3, 4, 5], maxvalue=4)
Traceback (most recent call last):
AssertionError: invalid combination

>>> lock = CombinationLock([])
Traceback (most recent call last):
AssertionError: invalid combination