This assignment is a tribute to the late Japanese puzzle maven Nobuyuki Yoshigahara (芦ヶ原 伸之 ,1936–2004). This brilliant guru, inventor, collector and solver of puzzles — commonly known in Japan as Nob — graduated from the Tokyo Institute of Technology in applied chemistry. After becoming disenchanted with his research career in high-polymer engineering, Nob turned to high school teaching as an educator of chemistry and mathematics.

nob
Nobuyuki Yoshigahara (芦ヶ原 伸之 ,1936–2004)

It is very difficult to give a simple and brief illustration to Nob's puzzle work since his ingenuity and diapason of his interests and achievements was quite incomparable. Numbers were a big passion of Nob, and his ingenuity in this field was amusing. In every number he could find some interesting rule or property. The following conundrum Nob considered as his masterpiece.

number puzzle
Nob's number puzzle

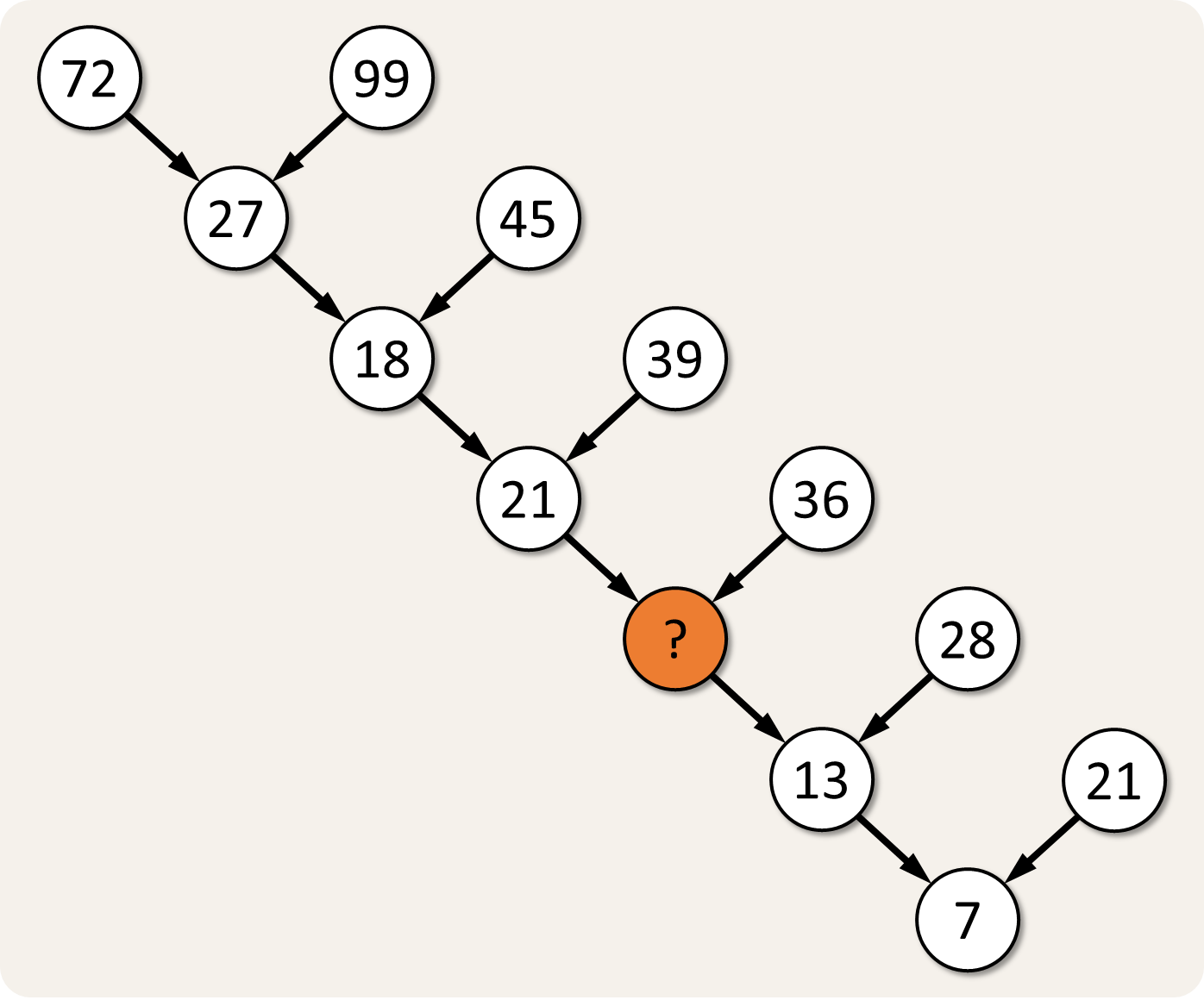
This puzzle is brilliant in its simplicity: the numbers that have been filled into the tree above are put in the nodes according to a certain rule. According to this rules, which number should be put instead of the question mark? Lee Sallows1 writes

You have to solve this yourself, otherwise you won't see how beautiful it is.

Don't think you have found the correct answer if the rule you came up with seems to suggest that there must be a typo in the puzzle. All numbers in the tree have been double checked and are correct.

At first sight the puzzle seems to be rather straightforward, prompting to put the number 15 at the position of the question mark. Unfortunately, in that case the pattern is broken by the lowest digit in the tree — the number 7.

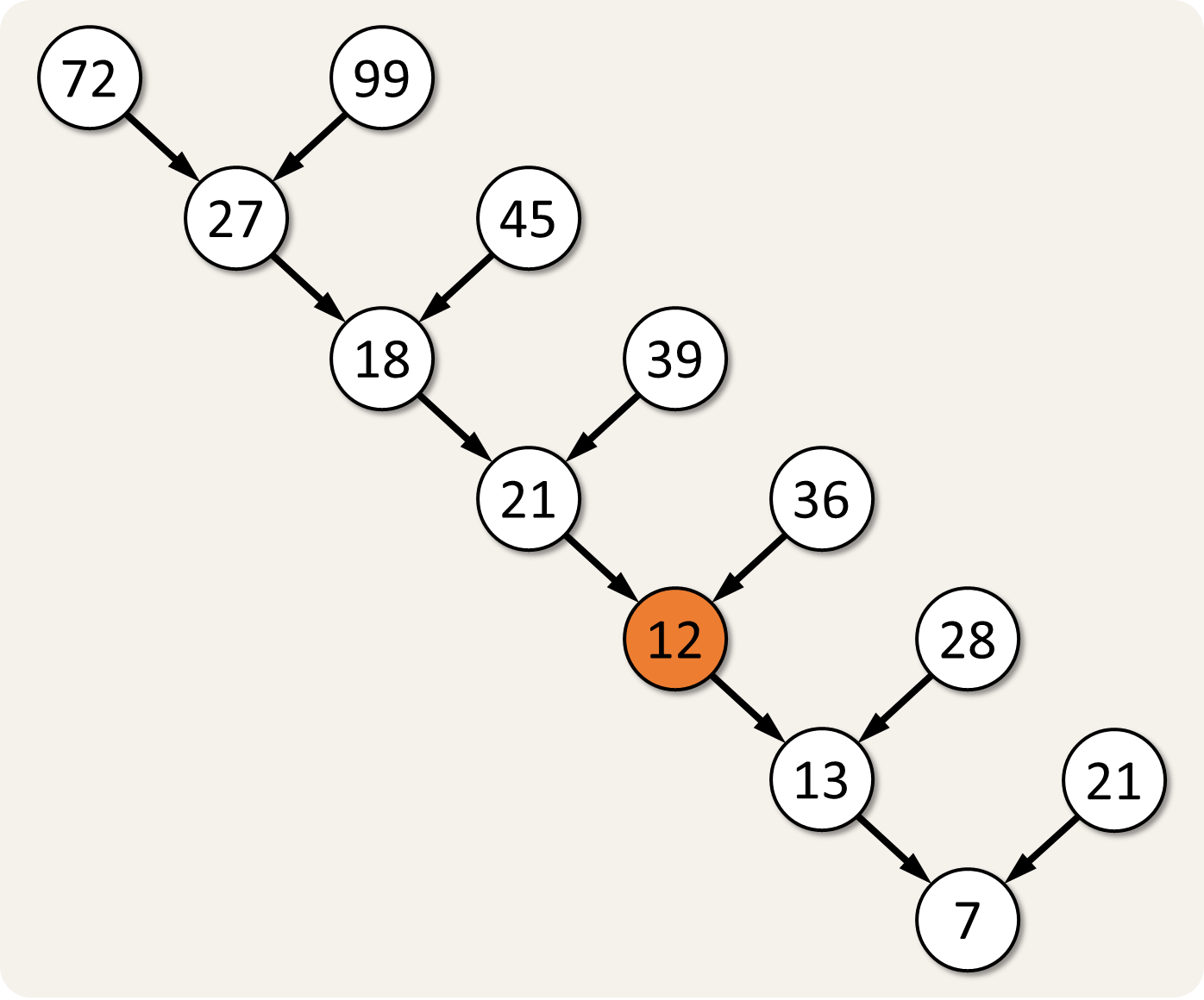
In fact the rule is different: all digits from the two numbers in any two circles pointing simultaneously to a third one need to be added to produce the resulting number in that circle. For example, the top two numbers give the sum $$7 + 2 + 9 + 9$$ resulting in the number $$27$$ that fills the underlying circle. The missing number can be computed according to the same rule: $$2 + 1 + 3 + 6 = 12$$.

getallenraadsel
Solution of Nob's number puzzle.

Input

The input contains a sequence of positive integers, each on a separate line. The sequence contains at least one integer and ends with the integer -1, which is not part of the actual sequence.

Output

The given sequence of integers are the top numbers in a tree, like the one used in the Nob's number puzzle. For the example at the bottom of this assignment, the given sequence of numbers is used to fill the nodes indicated in green in the figure below.

getallenraadsel
The program input are the top numbers in a tree, like the one used in the Nob's number puzzle.

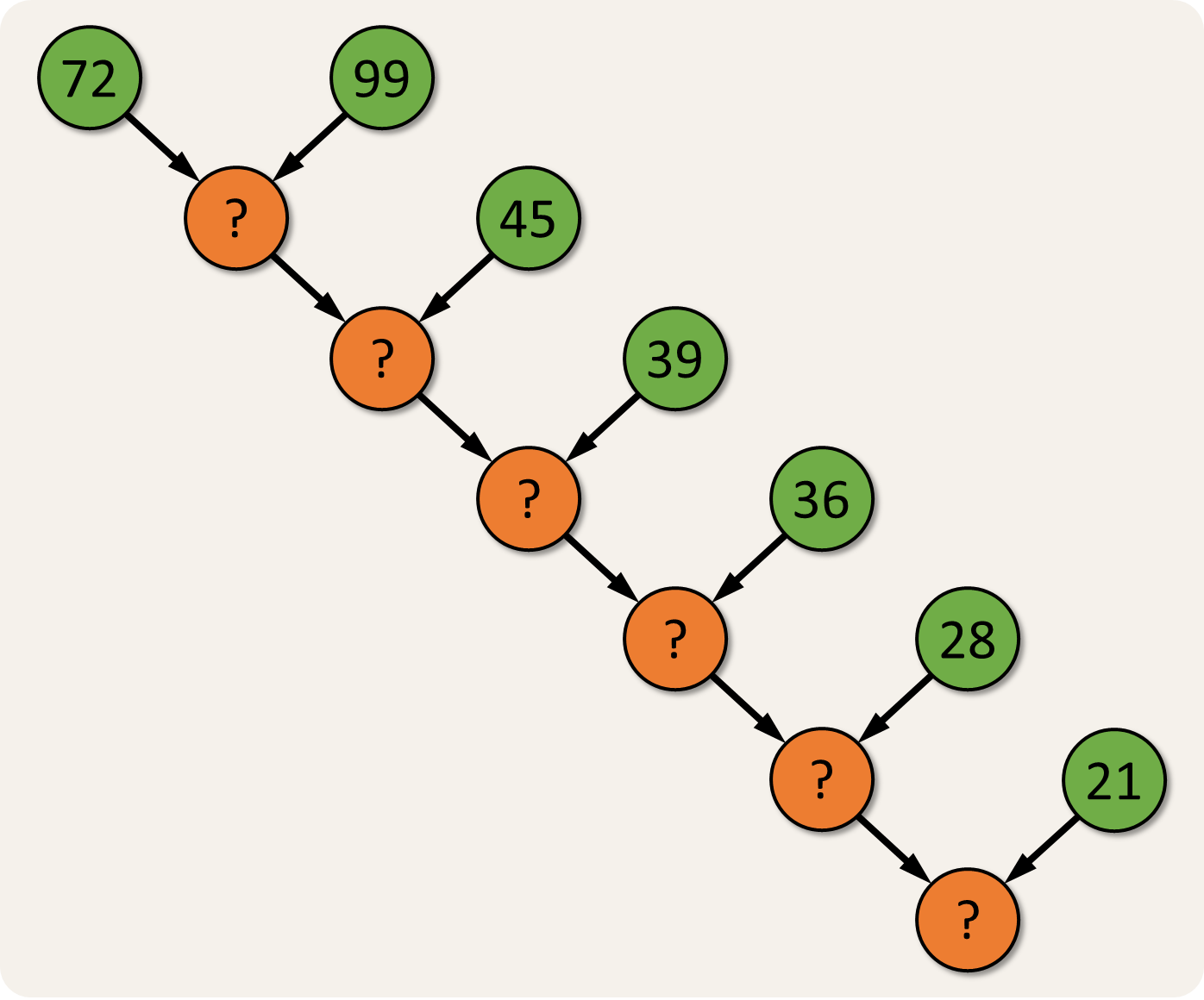
Your task is to complete the tree by filling up the missing numbers in the orange colored nodes. These missing numbers can be computed as the sum of the digits of the two numbers in the nodes above the orange nodes.

The output needs to be formatted in the following way. Each line contains two integers from the tree. The first line has no indentation, and each successive line has two additional spaces of indentation with respect to the previous line. The two numbers follow the indentation, with each number centered over four positions. None of the output lines may have spaces at the end of the line.

Example

Input:

72
99
45
39
36
28
21
-1

Output:

 72  99
   27  45
     18  39
       21  36
         12  28
           13  21
             7