The Eye of Horus is an ancient Egyptian symbol of protection, royal power and good health. The eye is personified in the goddess Wadjet. Different parts of the Eye of Horus were thought to be used by the ancient Egyptians to represent one divided by the first six powers of two, as shown in the image below.

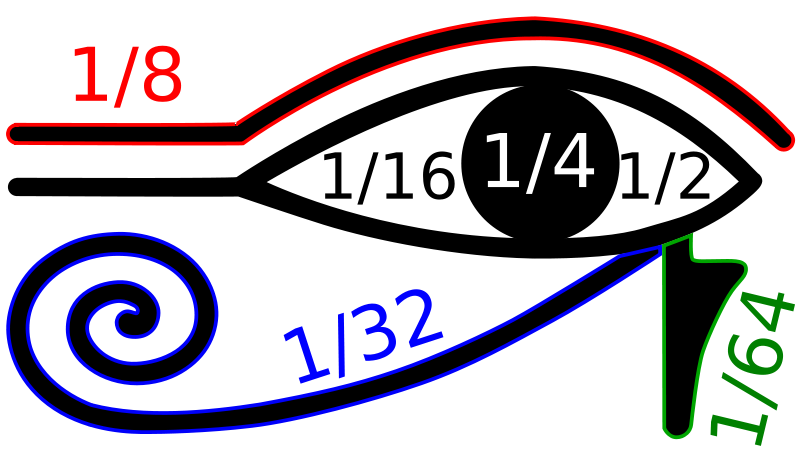
An Egyptian fraction is the sum of distinct unit fractions, such as $$\frac{1}{2} + \frac{1}{3} + \frac{1}{16}$$. That is, each fraction in the expression has a numerator equal to 1 and a denominator that is a positive integer, and all the denominators differ from each other. The value of an expression of this type is a positive rational number $$\frac{a}{b}$$. For instance, the Egyptian fraction above sums to $$\frac{43}{48}$$. It has been proven that every positive rational number can be represented by an Egyptian fraction.

Sums of this type were used as a serious notation for rational numbers by the ancient Egyptians, and continued to be used by other civilizations into medieval times. The Rhind Papyrus¹ of 500 BC already mentions these Egyptian fractions as an "ancient method" and they are thought to date back to the time of the early pyramids. Leonardo de Pisa's famous book Liber Abaci² of 1215 AD — which introduced the concept of zero to European mathematicians, the Hindu-Arabic system of numeration, and the famous rabbit sequence³ (Leonardo's nickname was Fibonacci) — also describes this kind of fraction decomposition. In modern mathematical notation, Egyptian fractions have been superseded by vulgar fractions and decimal notation.

An easy way to write a given fraction as an Egyptian fraction is to repeatedly take the largest unit fraction that will fit, subtract to find what remains, and repeat until the remainder is a unit fraction. For instance, 7 divided by 15 is less than $$\frac{1}{2}$$ but more than $$\frac{1}{3}$$, so the first unit fraction is $$\frac{1}{3}$$ and the first remainder is $$\frac{2}{15}$$. Then $$\frac{2}{15}$$ is less than $$\frac{1}{7}$$ but more than $$\frac{1}{8}$$, so the second unit fraction is $$\frac{1}{8}$$ and the second remainder is $$\frac{1}{120}$$. The latter fraction is itself a unit fraction, so we are finished: \[\frac{7}{15} = \frac{1}{3} + \frac{1}{8} + \frac{1}{120}\] During these computations we always use the irreducible version of a fraction $$\frac{a}{b}$$. A fraction is said to be irreducible if its numerator $$a$$ and denominator $$b$$ are coprime. A reducible fraction can be converted into an equivalent irreducible fraction by dividing both the numerator and the denominator by the greatest common divisor (gcd) of both integers. The gcd of two integers can be computed using the gcd function from the fractions module in the Python Standard Library.

>>> from fractions import gcd
>>> gcd(20, 8)
4

There are other algorithms for decomposing a given fraction than an Egyptian fraction, but there is no algorithm that guarantees a maximum number of terms or a minimum largest denominator. For instance, the greedy algorithm described above leads to \[\frac{5}{121} = \frac{1}{25} + \frac{1}{757} + \frac{1}{763309} + \frac{1}{873960180913} + \frac{1}{1527612795642093418846225}\] but a simpler rendering of the same number is \[\frac{5}{121} = \frac{1}{33} + \frac{1}{121} + \frac{1}{363}\]

Remark

For this exercise you have to make sure that you compute with fractions having integer numerators and denominators. As soon as you start working with floating point numbers to perform computations based on the decimal representation of the fractions, you will get into trouble because of rounding errors in the representation of floats.

Input

A fraction $$\frac{a}{b}$$, where the numerator $$a \in \mathbb{N_0}$$ and the denominator $$b \in \mathbb{N_0}$$ are on two separate lines. You may assume that $$0 < \frac{a}{b} \leq 1$$.

Output

The list of denominators of the decomposition of the fraction $$\frac{a}{b}$$ as an Egyptian fraction, using the greedy method described above. The denominators should be listed in increasing order, each on a separate line.

Example

Input:

47
60

Output:

2
4
30

Example

Input:

7
15

Output:

3
8
120

Example

Input:

5
41

Output:

9
93
11439