Telecommunications got an early start in France, where inventor Claude Chappe built a series of towers between Lille and Paris in 1792. Each tower was topped with a set of movable wooden arms that could be arranged to represent symbols. If each operator viewed his neighbor through a telescope, a symbol could pass through 15 stations covering 120 miles in only 9 minutes, giving France a valuable communications advantage over the surrounding powers during the sensitive period of the revolution.

This mechanical form of the Internet avant la lettre even makes an appearance in The Count of Monte-Cristo (Alexandre Dumas, 1844, original French title: Le Comte de Monte-Cristo):
They passed to the third story; it was the telegraph room. Monte Cristo looked in turn at the two iron handles by which the machine was worked. "It is very interesting," he said, "but it must be very tedious for a lifetime."
"Yes. At first my neck was cramped with looking at it, but at the end of a year I became used to it; and then we have our hours of recreation, and our holidays."
"Holidays?"
"Yes."
"When?"
"When we have a fog."
Expanded into a network of 534 stations, the system worked well, but it was expensive, with skilled operators manning towers set every 10-30 kilometers, and the messages were far from private. Finally the electrical telegraph killed it — Sweden abandoned the last commercial semaphore line in 1880. By then, depressed by illness and the conviction that others were stealing his ideas, Chappe had long since killed himself.
Assignment
Define a class Chappe that can be used to represent networks of telecommunication towers in Python. The objects of this class should at least support the following methods.
-
An initialization method that takes the location of a text file as its argument. You may assume that the text files makes use of a Unicode character set with UTF-8 encoding (see below). The file describes a network of towers that may communicate with each other. Each line of the file contains the names of two neighboring towers (indicated by the name of the city where the towers are located), separated from each other by a tab.
-
A method neighbours that takes the name of a tower (city) as its argument. The function must return the set containing the names of the neighboring towers (cities) in the network of the given tower (city).
-
A method hubs that takes two names of towers (cities) as its arguments. The method must return an integer that indicates the minimal number of times a symbol must be transmitted from one tower to a neighboring tower in the network, to sent the message between the two given towers. If a message cannot be sent between the two given towers — because they belong to two disconnected subnetworks — the function must return the value -1.
If the name of a tower is passed to the method neighbours or hubs that does not belong to the network represented by the object, an AssertionError must be raised with the message city not in network.
Algorithm
You can use the following algorithm to find the shortest path between tower1 and tower2 in a network:
-
Initialize $$U$$ = [tower1] as a list of towers whose neighbors still need to be processed, and $$P$$ = {tower1:0} as a dictionary that maps each processed tower onto the shortest distance from that tower to tower1.
-
Remove the first tower from $$U$$ and process its neighbors in the network by appending each unprocessed neighbor to $$U$$ and adding to $$P$$ the shortest distance from that unprocessed neighbour to tower1.
-
Keep repeating step 2 until a neighbors is reached that equals tower2 (figure out yourself how to obtain the distance to tower1) or until $$U$$ is empty (meaning that tower2 could not be reached from tower1).
Unicode files
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems. The standard consists of a set of code charts for visual reference, an encoding method and set of standard character encodings, a set of reference data computer files, and a number of related items, such as character properties, rules for normalization, decomposition, collation, rendering, and bidirectional display order (for the correct display of text containing both right-to-left scripts, such as Arabic and Hebrew, and left-to-right scripts).
Unicode can be implemented by different character encodings. The most commonly used encodings are UTF-8, UTF-16 and the now-obsolete UCS-2. UTF-8 uses one byte for any ASCII character, all of which have the same code values in both UTF-8 and ASCII encoding, and up to four bytes for other characters. To open a Unicode file in Python, you can pass the encoding used to the optional parameter encoding of the built-in function open. For example, in order to read the information from the Unicode text file chappe.txt that makes use of UTF-8 encoding, the file can be opened in the following way:
>>> open('chappe.txt', 'r', encoding='utf-8')Example
In the following interactive session we assume that the text file chappe.txt is in the current directory. This file contains a description of the network of towers that is graphically represented below. Note, for example, that the network has no connection between Avignon and Marseilles. As a result, no messages can be communicated between Lille and Marseille (they belong to two disconnected subnetworks).
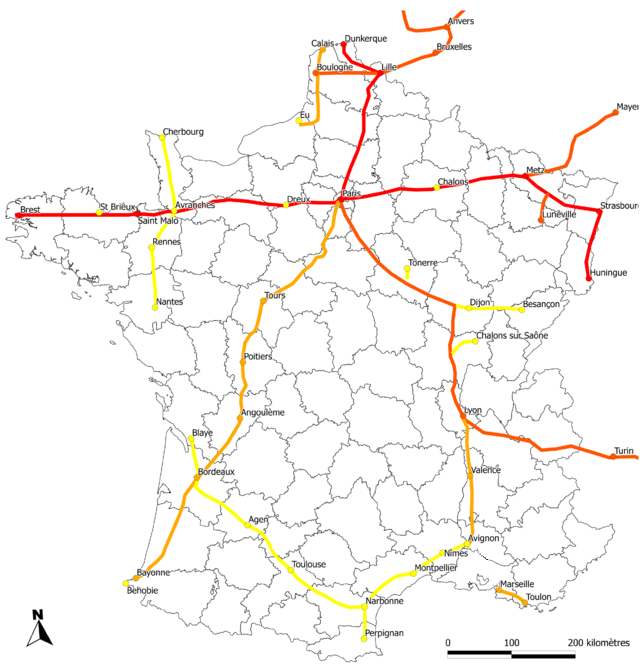
>>> network = Chappe('chappe.txt')
>>> network.neighbours('Lille')
{'Paris', 'Bruxelles', 'Dunkerque', 'Boulogne'}
>>> network. neighbours ('Paris')
{'Tours', 'Dreux', 'Tonerre', 'Lille'}
>>> network.neighbours('Brest')
{'St Brieux'}
>>> network.neighbours('Londres')
Traceback (most recent call last):
AssertionError: city not in network
>>> network.hubs('Lille', 'Lille')
0
>>> network.hubs('Lille', 'Tours')
2
>>> network.hubs('Lille', 'Toulouse')
11
>>> network.hubs('Lille', 'Montpellier')
9
>>> network.hubs('Lille', 'Perpignan')
11
>>> network.hubs('Lille', 'Marseille')
-1
>>> network.hubs('Lille', 'Londres')
Traceback (most recent call last):
AssertionError: city not in network