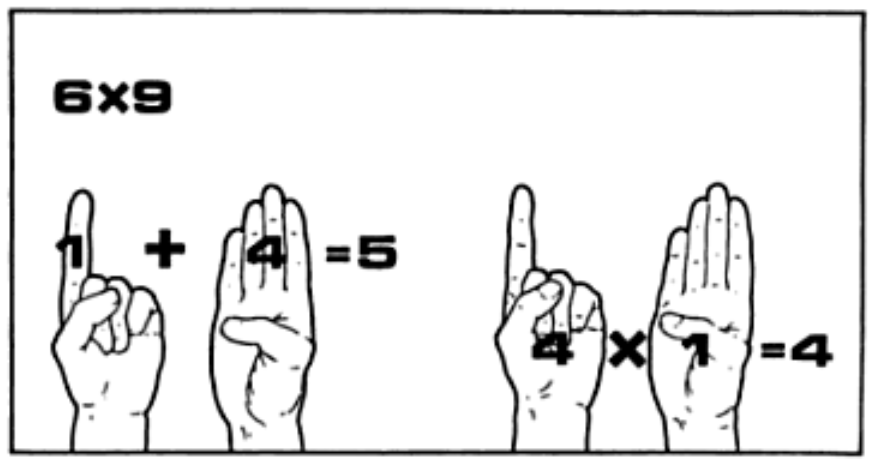
Here's a useful system of finger reckoning from the Middle Ages. To multiply $$6 \times 9$$, hold up one finger to represent the difference between the five fingers on that hand and the first number to be multiplied. On the other hand hold up four fingers, the difference between five and nine.
Then add the standing fingers and multiply the result by ten to get the tens of the answer \[ 10 \times (1 + 4) = 50 \] In this case there would be five tens, so one would know that the answer would be 50-something. To find the 'something' multiply the closed fingers \[ 4 \times 1 = 4 \] thus reaching the answer of 54. In this way one can multiply numbers between 6 and 9 while only knowing the multiplication table up to $$5 \times 5$$ and knowing how to multiply by 10.
A similar system could be used to multiply numbers between 10 and 15. To multiply $$14 \times 12$$ put up four fingers on one hand and two on the other. Add them to get six. Then add 10 times that sum to 100, which would give you 160. Finally add the product of the fingers $$(4 \times 2)$$ to reach the answer: 168. Again, this only requires to know the multiplication table up to $$5 \times 5$$ and to know how to multiply by 10.
Both finger reckoning techniques are a direct reflection of the fact that the following general algebraic equation holds for the multiplication of two integers $$x$$ and $$y$$ \[ xy = 100 + 10 [(x - 10) + (y - 10)] + (x - 10)(y - 10) \]
Input
Two integers $$x, y \in \mathbb{N}$$ ($$0 \leq x, y \leq 20$$), each on a separate line.
Output
A single line that describes how the two given integers can be multiplied using the finger reckoning techniques explained above. A distinction must be made between the following cases:
-
if both numbers are less than or equal to 5 or if at least one of the numbers is equal to 10, the product must be computed directly (see first example)
-
if both numbers are between 6 and 9 (including limits), the product must be computed using the first finger reckoning technique explained above (see second example)
-
if both numbers are between 11 and 15 (including limits), the product must be computed using the second finger reckoning technique explained above (see second example)
-
in all other cases the general algebraic equation to compute the product of two given integers must be used (see forth example)
Inspect the examples below to see how the output must be formatted.
Example
case: both numbers are less than or equal to 5
Input:
2
5Output:
2 x 5 = 10
Example
case: both number are between 6 and 9 (including limits)
Input:
6 9
Output:
6 x 9 = 10 x (1 + 4) + (4 x 1) = 54
Example
case: both number are between 11 and 15 (including limits)
Input:
14 12
Output:
14 x 12 = 100 + 10 x (4 + 2) + (4 x 2) = 168
Example
case: general algebraic equation to compute the product of two integers
Input:
4 11
Output:
4 x 11 = 100 + 10 x (-6 + 1) + (-6 x 1) = 44