Constrasten

• Bij meer complexe algemene lineaire modellen wenst men dikwijls meerdere hypothesen te toetsen.
• Bovendien vertalen de onderzoekshypotheses zich hierbij niet steeds in één parameter, maar in een lineaire combinatie van modelparameters.
• Een lineaire combinatie van modelparameters wordt ook een contrast genoemd.

NHANES voorbeeld

• Stel dat de onderzoekers de associatie tussen de leeftijd en de bloeddruk wensen te bestuderen. Mogelijks is die associatie anders is bij mannen dan vrouwen.

• De onderzoekers wensen de volgende onderzoeksvragen te beantwoorden:

  • Is er een associatie tussen leeftijd en de bloeddruk bij vrouwen?
  • Is er een associatie tussen leeftijd en de bloeddruk bij mannen?
  • Is de associatie tussen leeftijd en de bloeddruk verschillend bij mannen dan bij vrouwen?

Model

We fitten een model op basis van de gemiddelde systolische bloeddruk (BPSysAve) in functie van de leeftijd, geslacht en een interactie tussen leeftijd en geslacht voor volwassen blanke subjecten uit de NHANES studie.

library(NHANES)
bpData <- NHANES %>%
filter(
  Race1 =="White" &
    Age >= 18 &
    !is.na(BPSysAve)
    )

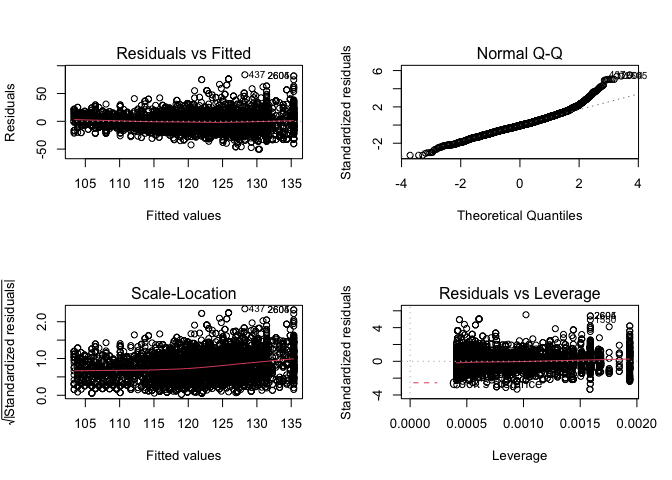
mBp1 <- lm(BPSysAve ~ Age*Gender, bpData)
par(mfrow = c(2,2))
plot(mBp1)

• Aannames van het model zijn niet voldaan!

  • lineariteit lijkt ok
  • heteroscedasticiteit
  • Geen normaliteit: scheve verdeling met staart naar rechts.
  • Grote dataset we kunnen steunen op de CLT

Transformatie

We fitten een model op basis van de log2 getransformeerde gemiddelde systolische bloeddruk (BPSysAve) in functie van de leeftijd, geslacht en een interactie tussen leeftijd en geslacht.

mBp2 <- lm(BPSysAve %>% log2 ~ Age*Gender, bpData)
par(mfrow = c(2,2))
plot(mBp2)

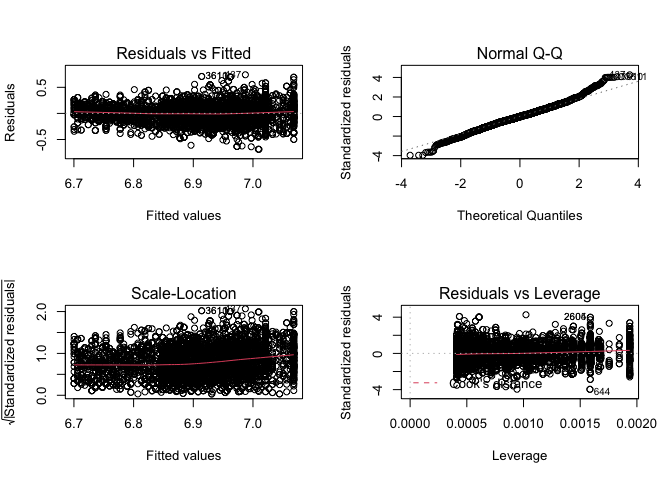
• De residuen tonen nog steeds heteroscedasticiteit.

Remediëren voor heteroscedasticiteit

• Als de plot van de residuen i.f.v. de geschatte waarden een toetervorm vertoont kan men toch correcte inferentie bekomen voor grote steekproeven als men de variantie van de response kan schatten.
• De inverse variantie voor elke observatie kan dan als gewicht worden gebruikt in de lm functie.

1. We zullen daarom de standard deviatie modelleren in functie van het gemiddelde.
2. Dat kan door de absolute waarde van de residuen te modelleren in functie van de gefitte waarden.
3. We kunnen de variantie van Y schatten voor elke observatie d.m.v de kwadraten van de predicties voor alle data punten a.d.h.v model voor de standard deviatie.
4. De inferentie blijft asymptotisch geldig.

mSd <- lm(mBp1$res %>% abs ~ mBp2$fitted)

We schatten het model nu opnieuw:

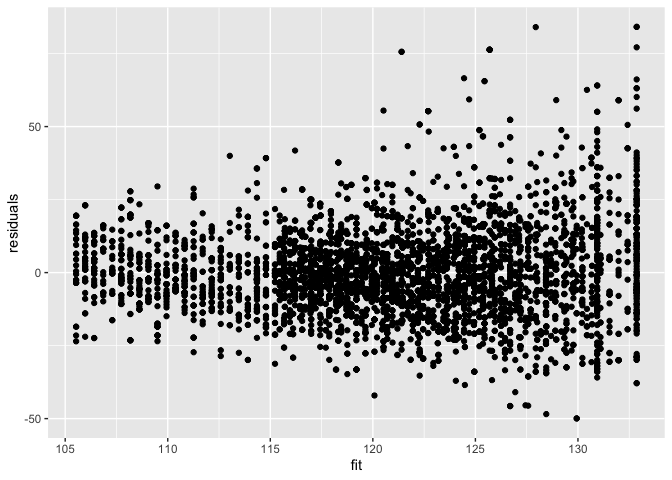
mBp3 <- lm(BPSysAve ~ Age*Gender, bpData, w = 1/mSd$fitted^2)

De residuen vertonen nog steeds heteroscedasticiteit.

data.frame(residuals = mBp3$residuals, fit = mBp3$fitted) %>%
  ggplot(aes(fit,residuals)) +
  geom_point()

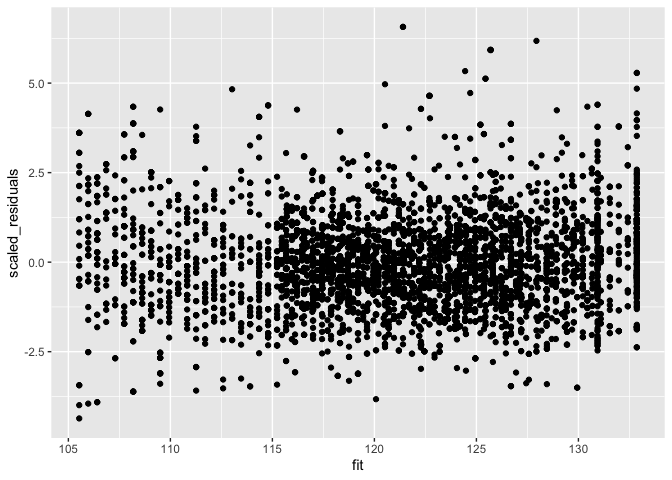
Na het herschalen van de residuen a.d.h.v. de standard deviatie (vermenigvuldigen met vierkantswortel van het gewicht) zijn de geschaalde residuen homoscedastisch.

De parameters worden geschat door de gewogen kleinste kwadraten techniek.

met \(w_i = 1/\hat \sigma^2_i\).

De gewogen regressie zal dus correct rekening houden met heteroscedasticiteit.

data.frame(scaled_residuals = mBp3$residuals/mSd$fitted, fit = mBp3$fitted) %>%
  ggplot(aes(fit,scaled_residuals)) +
  geom_point()