The Mercator projection is a cylindrical map projection¹ presented by the Flemish geographer and cartographer Gerardus Mercator² in 1569. It became the standard map projection for nautical navigation because of its ability to represent lines of constant course — known as rhumb lines³ or loxodromes — as straight segments that conserve the angles with the meridians. Although the linear scale is equal in all directions around any point, thus preserving the angles and the shapes of small objects (making it a conformal map projection⁴), the Mercator projection distorts the size of objects as the latitude increases from the Equator to the poles, where the scale becomes infinite. So, for example, landmasses such as Greenland and Antarctica appear much larger than they actually are relative to landmasses near the equator, such as Central Africa.

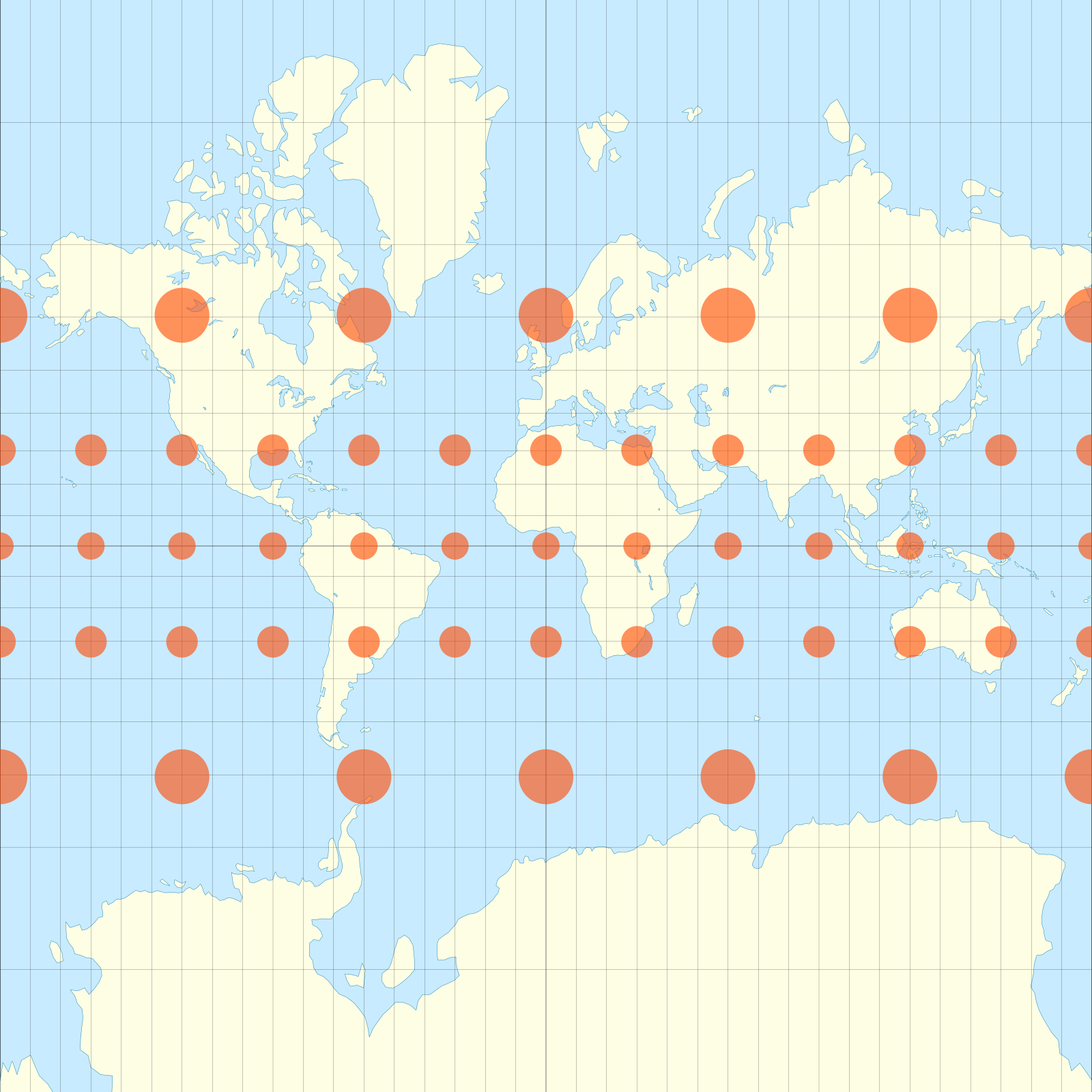
A point on Earth at longitude $$\lambda$$ and latitude $$\varphi$$ is mapped by the Mercator projection onto a point with coordinates $$(x, y)$$ on a rectangle with dimensions $$360 \times 180$$: \[ \begin{align} x &= (\lambda - \lambda_0 + 180)\!\!\!\!\mod{360} - 180 \\ \\ y &= 15 \cdot \ln\left(\frac{1 + \sin(\varphi)}{1 - \sin(\varphi)}\right) \end{align} \] The midpoint of the rectangle (with coordinates $$(0,0)$$) corresponds to a point on Earth at longitude $$\lambda_0$$ and latitude 0. The remainder upon integer division of $$x$$ by 360 is represented as $$x\!\!\!\!\mod{360}$$ and the function $$\ln$$ represents the natural logarithm.

Input

Three numbers $$\lambda_0, \lambda, \varphi \in \mathbb{R}$$ that describe angles (in degrees). Each number is given on a separate line.

Output

The Mercator projection $$(x, y)$$ of a point on Earth at longitude $$\lambda$$ and latitude $$\varphi$$ onto a rectangle with dimensions $$360 \times 180$$. The midpoint of the rectangle (with coordinates $$(0,0)$$) corresponds to a point on Earth at longitude $$\lambda_0$$ and latitude 0.

The $$x$$ and $$y$$ coordinates are printed on separate lines and preceded by the letter x (resp. letter y), a colon (:) and a space.

Example

Input:

0.0
10.0
45.0

Output:

x: 10.0
y: 26.441207610586293