Gegeven is het voorschrift van een tweedegraadsfunctie $$f$$:

Wil je de grafiek van $$f$$ tekenen, dan kan je ofwel een programma als Geogebra¹ gebruiken (zie afbeelding) of je kan zelf op onderzoek uitgaan of een analyse uitvoeren.

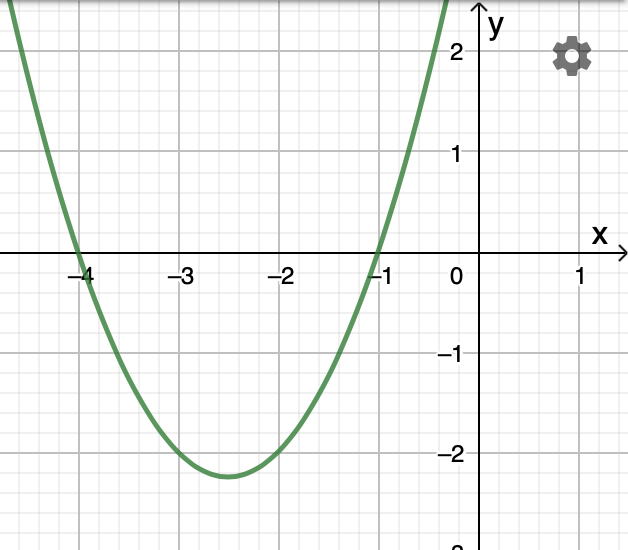
Een eerste stap om de grafiek van de functie te tekenen, is het bepalen van de nulpunten. Bij het berekenen van de nulpunten van een tweedegraadsfunctie, moet je eerst de discriminant berekenen.

Discriminant

Stel dat het voorschrift van een tweedegraadsfunctie gegeven wordt door

Dan bereken je de discriminant m.b.v. volgende formule:

Opgave

Vraag aan de gebruiker van je programma achtereenvolgens de coëfficiënten $$a$$, $$b$$ en $$c$$. Geef de discriminant terug.

Voorbeeld

1
5
4

9.0