Predictie-intervallen

Het geschatte regressiemodel kan ook worden gebruikt om een predictie te maken voor één uitkomst van één experiment waarbij een nieuwe uitkomst $Y^*$ bij een gegeven $x$ zal geobserveerd worden. Het is belangrijk in te zien dat dit experiment nog moet worden uitgevoerd. We wensen dus een nog niet-geobserveerde individuele uitkomst te voorspellen.

Aangezien $Y^*$ een nieuwe, onafhankelijke observatie voorstelt, weten we dat

\[Y^* = g(x) + \epsilon^*\]

met $\epsilon^*\sim N(0,\sigma^2)$ en $\epsilon^*$ onafhankelijk van de steekproefobservaties $Y_1,\ldots, Y_n$.

We weten dat $\hat{g}(x)$ een schatting is van de gemiddelde log-S100A8 expressie bij de log-ESR1 expressie $x$, met name een schatting van het conditioneel gemiddelde $\text{E}[Y\vert x]$. We argumenteren nu dat $\hat{g}(x)$ ook een goede predictie is van een nieuwe log-S100A8 expressiewaarde $Y^*$ bij een gegeven log-ESR1 expressieniveau $x$.

We weten reeds dat $\hat{g}(x)$ een schatting is van $\text{E}[Y\vert x]$, wat het punt op de regressierechte bij $x$ voorstelt. Het regressiemodel stelt dat bij een gegeven $x$, de individuele uitkomsten $Y$ Normaal verdeeld zijn rond dit punt op de regressierechte. Aangezien een Normale verdeling symmetrisch is, is het even waarschijnlijk om een uitkomst groter dan $\text{E}[Y\vert x]$ te observeren, als een uitkomst kleiner dan $\text{E}[Y\vert x]$ te observeren. We beschikken echter niet over meer informatie dat ons zou toelaten om te vermoeden dat een uitkomst eerder groter, dan wel kleiner dan $\text{E}[Y\vert x]$ zou zijn. Om die reden is het punt op de (geschatte) regressierechte de beste predictie van een individuele uitkomst bij een gegeven $x$.

We voorspellen dus een nieuwe log-S100A8 meting bij een gekend log2-ESR1 expressieniveau x door

\[\hat{y}(x)=\hat{\beta}_0+\hat{\beta}_1 \times x\]

Merk op dat $\hat{y}(x)$ eigenlijk numeriek gelijk is aan $\hat{g}(x)$. Gezien het verschil in interpretatie tussen een predictie en een schatting van een conditioneel gemiddelde, gebruiken we een andere notatie.

Hoewel de geschatte gemiddelde uitkomst en de predictie voor een nieuwe uitkomst gelijk zijn, zullen hun steekproefdistributies echter verschillend zijn: de onzekerheid op de geschatte gemiddelde uitkomst wordt gedreven door de onzekerheid op de parameterschatters $\hat\beta_0$ en $\hat\beta_1$. De onzekerheid op de ligging van een nieuwe observatie, daarentegen, wordt gedreven door de onzekerheid op het geschatte gemiddelde en de bijkomende onzekerheid ten gevolge van het feit dat nieuwe observaties at random variëren rond de het conditionele gemiddelde (de regressie rechte) met een variantie $\sigma^2$. De nieuwe observatie is eveneens onafhankelijk van de observaties in de steekproef zodat de error $\epsilon$ onafhankelijk zal zijn van de schatter van de gemiddelde uitkomst $\hat{g}(x)$. De standard error op een predictie voor een nieuwe observatie wordt dus

\[\text{SE}_{\hat{Y}(x)}=\sqrt{\hat\sigma^2+\hat\sigma^2_{\hat{g}(x)}}=\sqrt{MSE\left\{1+\frac{1}{n}+\frac{(x-\bar X)^2}{\sum\limits_{i=1}^n (X_i-\bar X)^2}\right\}}.\]

Opnieuw kan worden aangetoond dat de statistiek

\[\frac{\hat{Y}(x)-Y}{\text{SE}_{\hat{Y}(x)}}\sim t_{n-2}\]

een t-verdeling volgt met n-2 vrijheidsgraden. Deze statistiek kan gebruikt worden om een betrouwbaarheidsinterval op de predictie te construeren, ook wel een predictie-interval (PI) genoemd. Merk op dat dit predictie-interval een verbeterde versie is van een referentie-interval wanneer de modelparameters niet gekend zijn. Het PI houdt immers rekening met de onzekerheid op het geschatte gemiddelde (gebruik van standard error op predictie i.p.v. standaard deviatie) en deze op de geschatte standaard deviatie (gebruik van t-verdeling i.p.v Normale verdeling).

Predicties en predictie-intervallen (PIs) kunnen opnieuw eenvoudig worden verkregen in R via de predict(.) functie. De predictorwaarden (x-waarden) voor het berekenen van de predicties worden opnieuw meegegeven via het newdata argument. PIs op de predicties kunnen worden verkregen d.m.v. het argument interval="prediction".

grid <- log2(140:4000)
p <- predict(
  lm2,
  newdata = data.frame(log2ESR1=grid),
  interval="prediction")
head(p)

##        fit      lwr      upr
## 1 11.89028 9.510524 14.27004
## 2 11.87370 9.495354 14.25205
## 3 11.85724 9.480288 14.23419
## 4 11.84089 9.465324 14.21646
## 5 11.82466 9.450461 14.19886
## 6 11.80854 9.435698 14.18138

De predicties en hun 95% puntgewijze predictie-intervallen kunnen eveneens grafisch worden weergegeven (Figuur 35). Merk op dat de intervallen veel breder zijn dan de betrouwbaarheidsintervallen. Merk ook op dat de meeste observaties binnen de predictie-intervallen liggen. We verwachten inderdaad gemiddeld 95% van de observaties binnen de predictie-intervallen. Dat is niet zo voor de betrouwbaarheidsintervallen, die immers geen informatie geven over de verwachte locatie van een nieuwe observatie, maar wel over waar men het conditioneel gemiddelde verwacht op basis van de steekproef!

preddata <- data.frame(cbind(grid = grid,p))
brca %>% ggplot(aes(x=log2ESR1,y=log2S100A8)) +
  geom_point() +
  geom_smooth(method="lm", color = "black") +
  geom_line(
    aes(x = grid,y = lwr),
    preddata,
    color="red") +
  geom_line(
    aes(x = grid,y = upr),
    preddata,
    color="red")

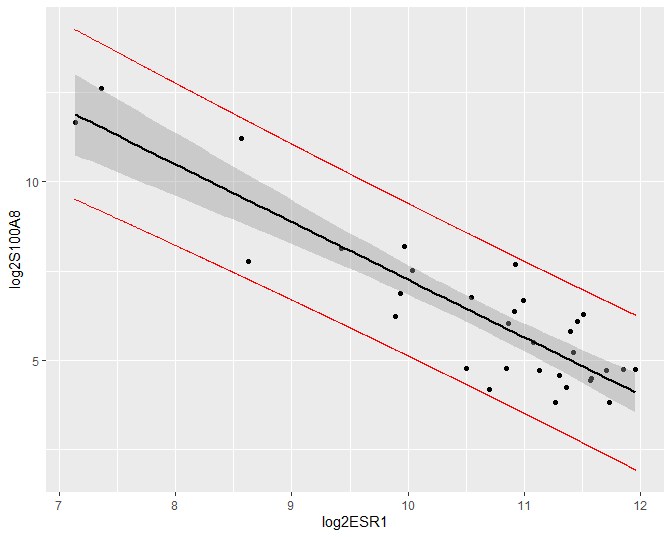
Figuur 35: Scatterplot voor log2-S100A8 expressie in functie van de log2-ESR1 expressie met model voorspellingen en 95$$\%$$ betrouwbaarheidsintervallen en 95$$\%$$ predictie-intervallen. Rode lijn: predictie interval, grijze band: betrouwbaarheidsinterval, zwarte lijn: lineair model