A mathematical constant is a key number whose value is fixed by an unambiguous definition. The constant is often referred to by a symbol (e.g. an alphabet letter) or named after a mathematician to facilitate using it across multiple mathematical problems.
For example, Archimedes' constant is denoted by the Greek letter $$\pi$$ and defined as the ratio of the length of a circle's circumference to its diameter.
The following table lists some mathematical constants and their decimal expansion, ordered by year of discovery.
| name | symbol | decimal expansion | year |
|---|---|---|---|
| Archimedes' constant | $$\pi$$ | 3.14159265358979323846 | 1900–1600 BCE. |
| golden ratio | $$\phi$$ | 1.61803398874989484820 | ~300 BCE |
| Champernowne constant | $$\text{C}_{10}$$ | 0.12345678910111213141 | 1933 |
| Feigenbaum constant | $$\delta$$ | 4.66920160910299067185 | 1975 |
Assignment
The pyramidal representation of a mathematical constant $$\alpha$$ consists of $$n \in \mathbb{N}_0$$ steps, that are numbered from top to bottom, starting from 1. The $$i$$-th step ($$i = 1, 2, \ldots, n$$) contains $$i$$ numbers, each of which is the sum of the next $$i$$ digits of $$\alpha$$. For example, these are the pyramidal representations with 5 steps of the four constants $$\pi$$, $$\phi$$, $$\text{C}_{10}$$ and $$\delta$$.
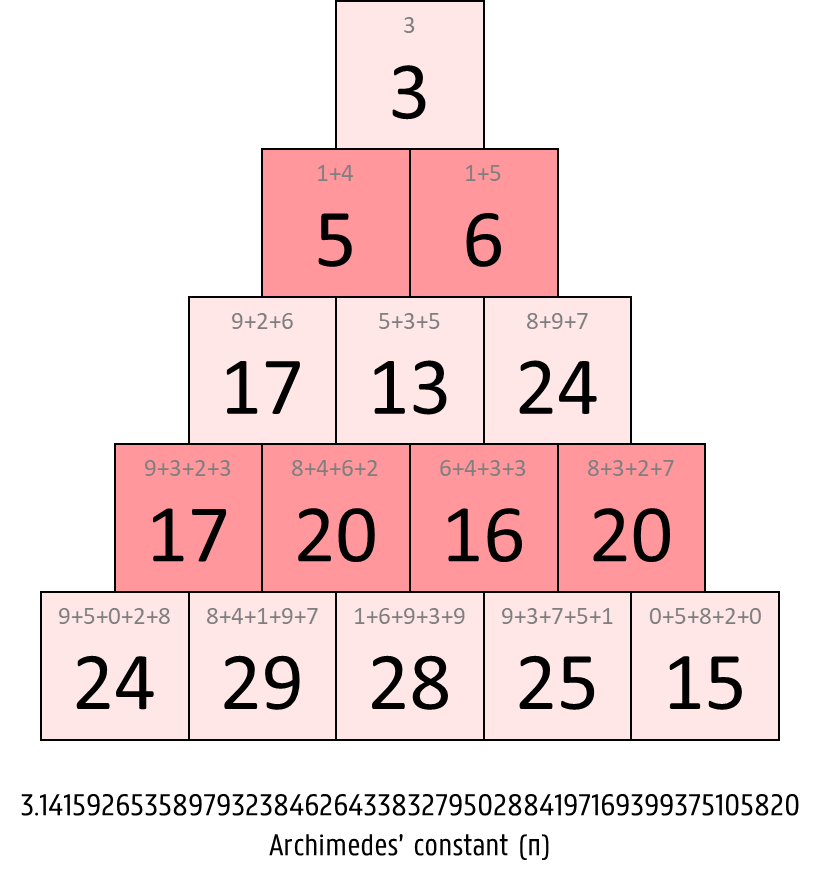
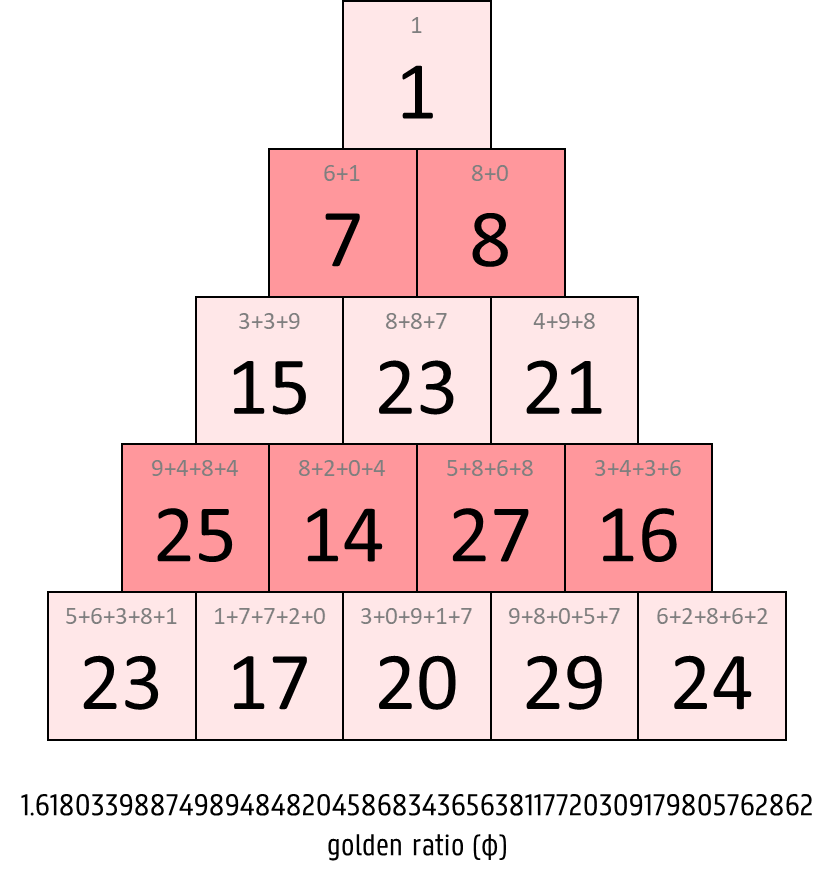
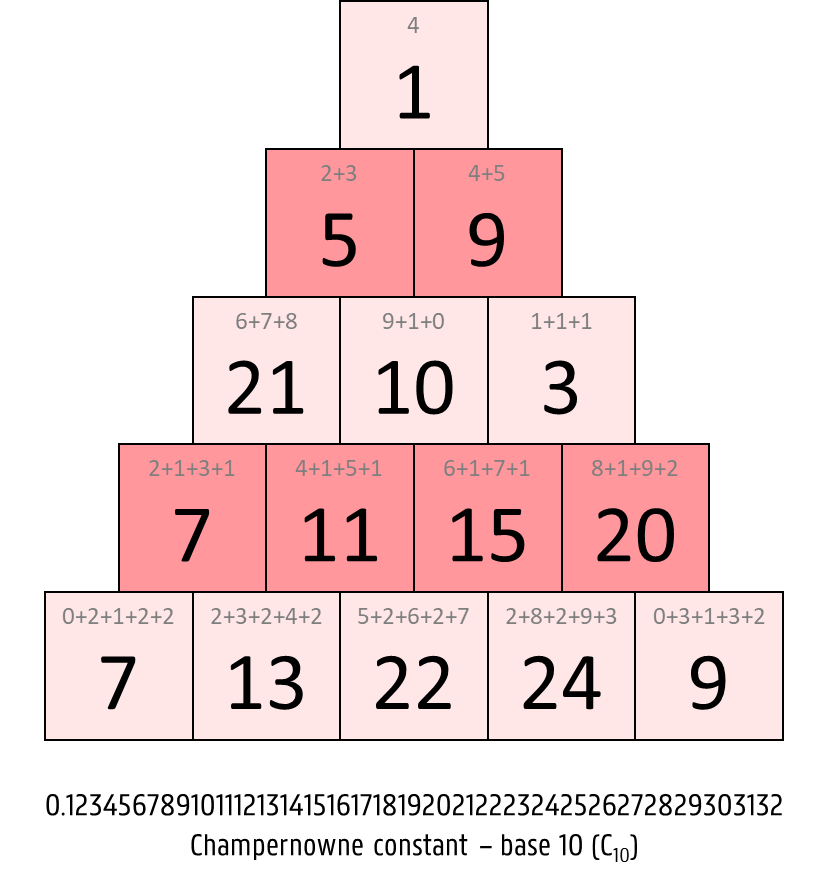
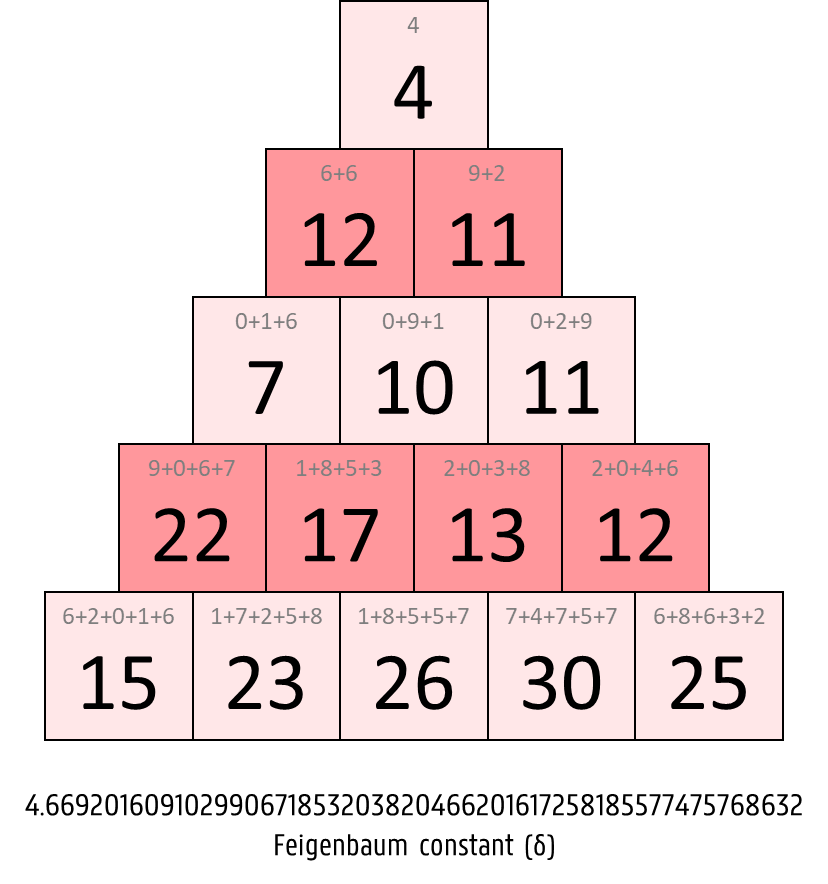
To determine the consecutive digits of $$\alpha$$, the mathematical constant is first cleaned up in the following way. If $$\alpha$$ is a real-valued number, its decimal dot is removed. If $$\alpha$$ is negative, the minus sign is removed. All leading zeros are also removed from the obtained number. In other words, we only use the significant digits of $$\alpha$$.
Input
The first line contains the decimal expansion of a mathematical constant $$\alpha$$. The second line contains a number $$n \in \mathbb{N}_0$$.
Output
The pyramidal representation of $$\alpha$$ with $$n$$ steps. Each step is on a separate line. The numbers on the same step are separated from each other by a single space.
Note
You may assume that sufficient digits of $$\alpha$$ are given to determine its pyramidal representation with $$n$$ steps.
Example ($$\pi$$, Archimedes' constant)
Input:
3.141592653589793238462643383279502884197169399375105820
5Output:
3
5 6
17 13 24
17 20 16 20
24 29 28 25 15Epilogue
NASA1 only uses 15 digits of $$\pi$$ for calculating interplanetary travel. At 40 digits, you could calculate the circumference of a circle the size of the visible universe with an accuracy that'd fall off by less than the diameter of a single hydrogen atom.
