A Letter Boxed¹ puzzle consists of a square with one or more letters along each side. The same letter never appears more than once.

A Letter Boxed puzzle with three letters along each side of the square.

You find a solution by connecting the letters around the square to form a sequence of words which is

complete: all letters around the square are used at least once
consecutive: the last letter of each word (except the last) is also the first letter of the next word
crossing: consecutive letters in a word cannot be along the same side of the square

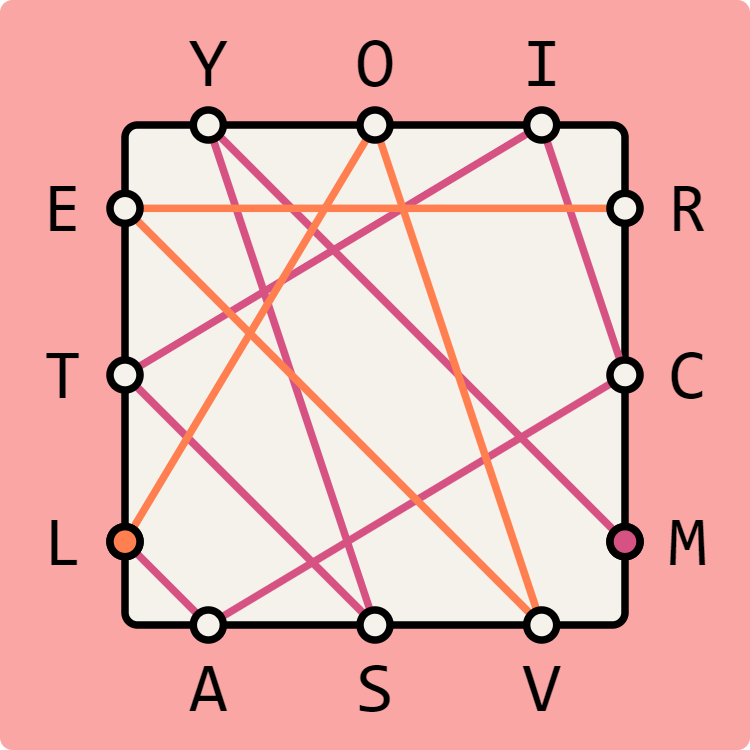
The same letter can be use more than once to solve the puzzle. As such, the three colors MYSTIC, CORAL and LIVER form a solution to the above puzzle.

The three colors MYSTIC, CORAL and LIVER form a solution to the Letter Boxed puzzle. Consecutive letters of these words are connected by a line whose color corresponds to the word of the solution in which the two letters appear consecutively. The circles near the initial letters of each word are also filled with that color.

Consecutive letters of these words are connected by a line whose color corresponds to the word of the solution in which the two letters appear consecutively. The circles near the initial letters of each word are also filled with that color.

Assignment

Both the letter arrangement and a possible solution of a Letter Boxed puzzle are represented as a sequence of words: a string (str) with one or more words separated by hyphens (-), where each word consists of one or more uppercase letters.

With the letter arrangement of a puzzle, the words consist of the letters that are along the same side of the square. For example, the letter arrangement of the puzzle from the introduction is represented as YOI-RCM-VSA-LTE and its solution as MYSTIC-CORAL-LIVER. The sides of the square are numbered from zero based on the representation of the letter arrangement. For example, in the letter arrangement YOI-RCM-VSA-LTE the letter O is along side 0, the letter V along side 2 and the letter E along side 3.

Your task:

Write a function side that takes two arguments: i) an uppercase letter $$l$$ (str) and ii) the letter arrangement of a puzzle. The function must return the number (int) of the side along which the letter $$l$$ appears around the square of the puzzle, or the value -1 (int) if letter $$l$$ does not appear around the square of the puzzle.
Write a function iscomplete that takes two arguments: i) a possible solution of a puzzle and ii) the letter arrangement of the puzzle. The function must return a Boolean value (bool) that indicates if the possible solution is complete.
Write a function isconsecutive that takes a possible solution of a puzzle. The function must return a Boolean value (bool) that indicates if the possible solution is consecutive.
Write a function iscrossing that takes two arguments: i) a possible solution of a puzzle and ii) the letter arrangement of the puzzle. The function must return a Boolean value (bool) that indicates if the possible solution is crossing.
Write a function issolution that takes two arguments: i) a possible solution of a puzzle and ii) the letter arrangement of the puzzle. The function must return a Boolean value (bool) that indicates if the possible solution is actually a solution of the puzzle.

Example

        >>> side('O', 'YOI-RCM-VSA-LTE')
0
>>> side('V', 'YOI-RCM-VSA-LTE')
2
>>> side('E', 'YOI-RCM-VSA-LTE')
3
>>> side('X', 'YOI-RCM-VSA-LTE')
-1

>>> iscomplete('MYSTIC-CORAL-LIVER', 'YOI-RCM-VSA-LTE')
True
>>> iscomplete('DENIM-MAIZE-EGGPLANT', 'GND-IET-MZL-AP')
True
>>> iscomplete('GAINSBORO-ONYX-PEAR', 'BGY-NXE-PAO-SRI')
True
>>> iscomplete('KOBI-PLATINUM-ZOMP', 'TML-OZB-IUK-APN')
True
>>> iscomplete('DESERT-TEAL-LIVID', 'SIT-EVW-ADC-KLR')
False
>>> iscomplete('RUFOUS-SKOBELOFF', 'FL-XUM-SKE-BOR')
False
>>> iscomplete('DENIM-OPAL-MANDARIN', 'NMO-AI-LDR-EYP')
False
>>> iscomplete('BONE-SEPIA-BROWN', 'ODI-VAR-BEP-SNW')
False

>>> isconsecutive('MYSTIC-CORAL-LIVER')
True
>>> isconsecutive('DENIM-MAIZE-EGGPLANT')
True
>>> isconsecutive('GAINSBORO-ONYX-PEAR')
False
>>> isconsecutive('KOBI-PLATINUM-ZOMP')
False
>>> isconsecutive('DESERT-TEAL-LIVID')
True
>>> isconsecutive('RUFOUS-SKOBELOFF')
True
>>> isconsecutive('DENIM-OPAL-MANDARIN')
False
>>> isconsecutive('BONE-SEPIA-BROWN')
False

>>> iscrossing('MYSTIC-CORAL-LIVER', 'YOI-RCM-VSA-LTE')
True
>>> iscrossing('DENIM-MAIZE-EGGPLANT', 'GND-IET-MZL-AP')
False
>>> iscrossing('GAINSBORO-ONYX-PEAR', 'BGY-NXE-PAO-SRI')
True
>>> iscrossing('KOBI-PLATINUM-ZOMP', 'TML-OZB-IUK-APN')
False
>>> iscrossing('DESERT-TEAL-LIVID', 'SIT-EVW-ADC-KLR')
True
>>> iscrossing('RUFOUS-SKOBELOFF', 'FL-XUM-SKE-BOR')
False
>>> iscrossing('DENIM-OPAL-MANDARIN', 'NMO-AI-LDR-EYP')
True
>>> iscrossing('BONE-SEPIA-BROWN', 'ODI-VAR-BEP-SNW')
False

>>> issolution('MYSTIC-CORAL-LIVER', 'YOI-RCM-VSA-LTE')
True
>>> issolution('DENIM-MAIZE-EGGPLANT', 'GND-IET-MZL-AP')
False
>>> issolution('GAINSBORO-ONYX-PEAR', 'BGY-NXE-PAO-SRI')
False
>>> issolution('KOBI-PLATINUM-ZOMP', 'TML-OZB-IUK-APN')
False
>>> issolution('DESERT-TEAL-LIVID', 'SIT-EVW-ADC-KLR')
False
>>> issolution('RUFOUS-SKOBELOFF', 'FL-XUM-SKE-BOR')
False
>>> issolution('DENIM-OPAL-MANDARIN', 'NMO-AI-LDR-EYP')
False
>>> issolution('BONE-SEPIA-BROWN', 'ODI-VAR-BEP-SNW')
False

Assignment

Example

Epilogue