What secret message is hidden in this grid?

The message is "East, west, home's best.". A so-called grille is used to decode the message: a pierced sheet (of paper or cardboard or similar) with a square grid into which some apertures are pierced. In this case, a $$5 \times 5$$ grid into which six apertures are pierced according to the following pattern.
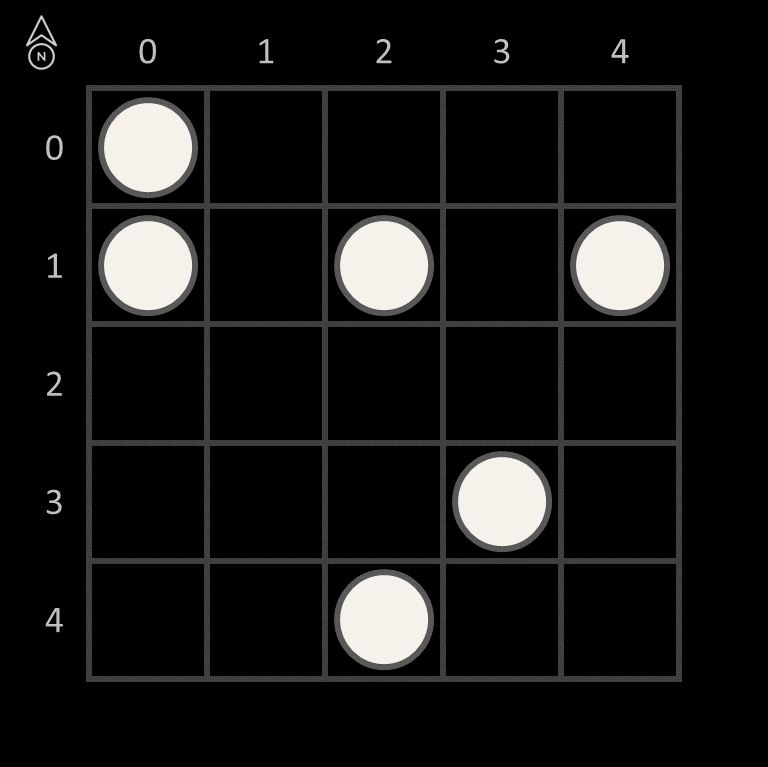
If the grille is placed on top of the square grid, the text "East, " can be read through the apertures (in reading order from left to right, and from top to bottom). This is the first fragment of the hidden message.
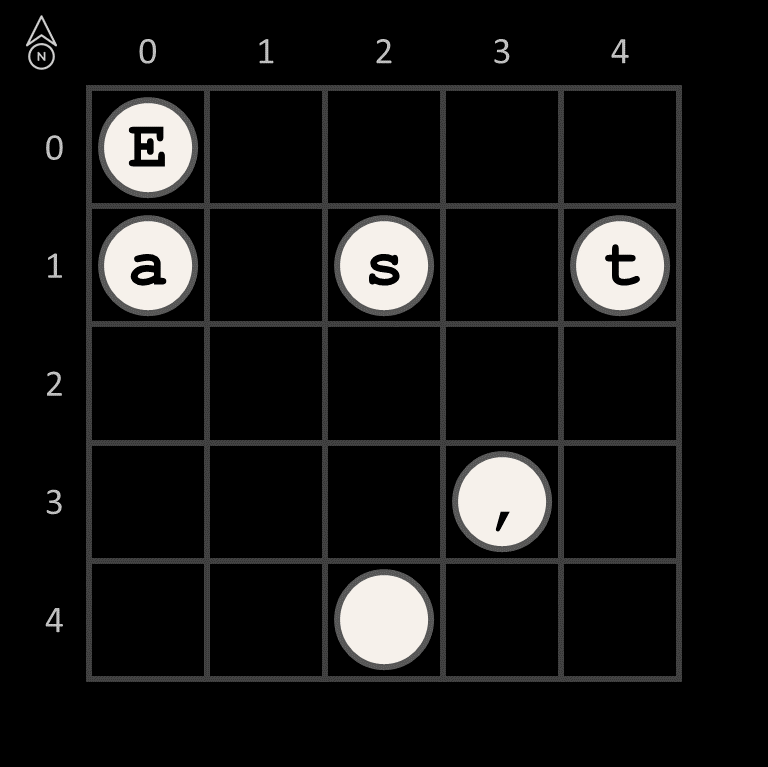
By rotating the grille 90° clockwise, the second fragment of the hidden message can be read: "West, ". After that, the grille can be rotated 90° clockwise twice more to read the final two fragments of the hidden message: "home's" and " best."
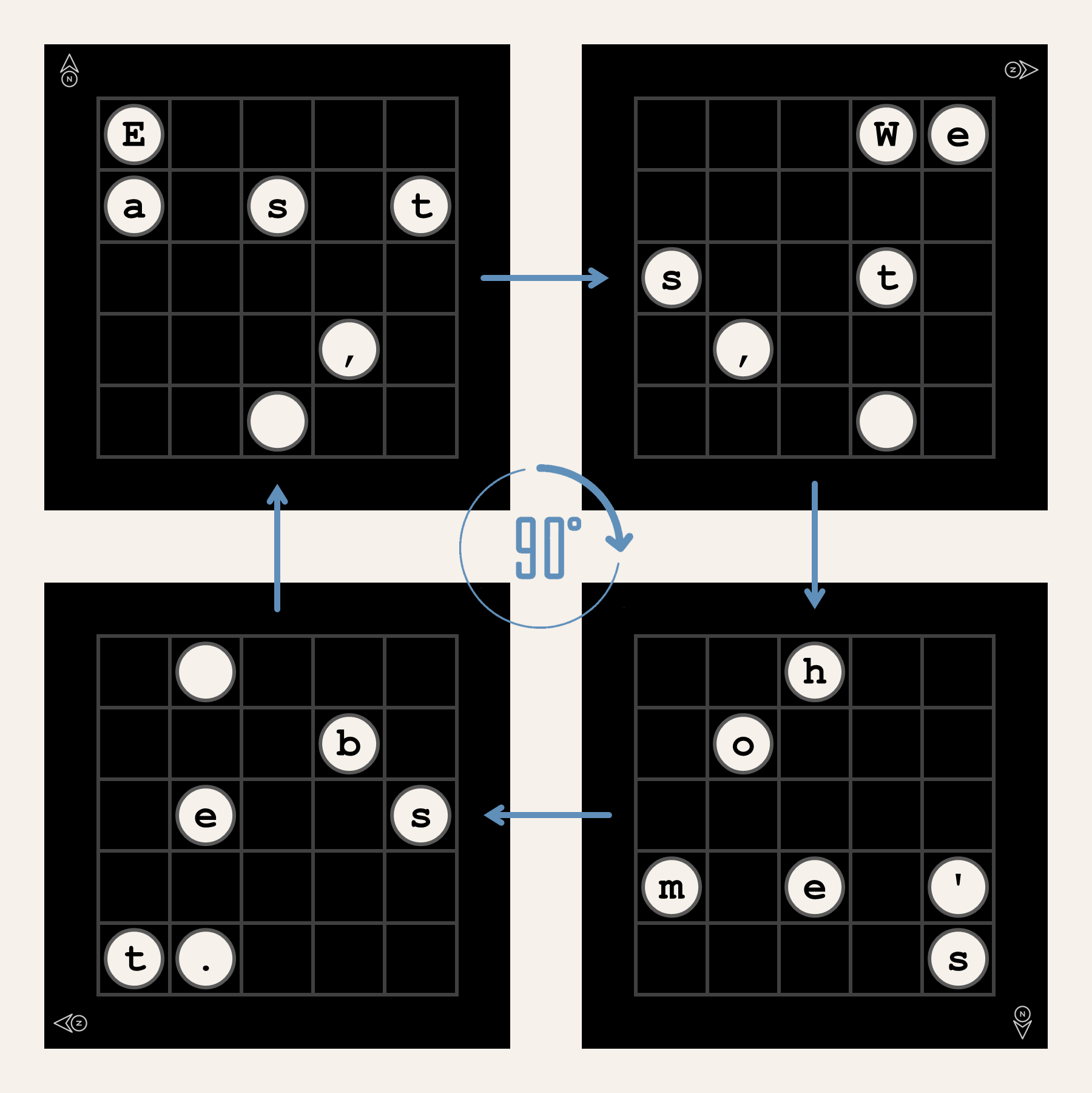
The earliest known description of this technique is due to the Italian polymath Girolamo Cardano1 in 1550. For that reason, grilles are sometimes called Cardan grilles.
Assignment
In order to be able to refer to the cells of a grid (both for a grid with characters in which a secret message is hidden and for a grid with the apertures of a grille), the rows are numbered from top to bottom, and the columns from left to right, starting at zero in both cases. As a result, the position of a cell can be represented as a tuple $$(r, c)$$, with $$r \in \mathbb{N}$$ (int) indicating the row index and $$c \in \mathbb{N}$$ (int) indicating the column index.
An $$n \times n$$ ($$n \in \mathbb{N}_0$$) grid that hides a secret message is stored in a text file. Each row of the grid is on a separate line, so that the file has $$n$$ lines that each contain $$n$$ characters. For example, the file containing the $$5 \times 5$$ grid that hides the secret message from the introduction, looks like this:
E hWe aosbt seVts m,e,' t. s
Define a class Grille to represent grilles that can be used to decode secret messages. Two arguments must be passed when creating a grille (Grille): i) the number of rows/columns (int) of the square grid on the grille and ii) a collection (list, tuple or set) with the positions of the apertures in the grille. A grille $$g$$ (Grille) must at least have the following properties:
-
dimension: number of rows/columns (int) of the square grid on grille $$g$$
-
apertures: set with the positions of the apertures in grille $$g$$
In addition, a grille $$g$$ (Grille) must at least support the following methods:
-
A method decode that takes the location (str) of a text file containing a square grid that hides a secret message. The method must return the fragment of the secret message (str) that can be read through the apertures (in reading order from left to right, and from top to bottom) when putting grille $$g$$ on top of the grid.
-
A method rotate with an optional parameter clockwise that may take a Boolean value (bool). Based on the value of the parameter clockwise, the method must rotate grille $$g$$ 90° clockwise (True, default value) or counterclockwise (False). The method must return a reference to grille $$g$$.
Tip: rotate 90°
If an $$n \times n$$ grid is rotated 90° clockwise, a cell at position $$(r, c)$$ ends up at position $$(c, n - r - 1)$$ (see orange cell in the figure below).
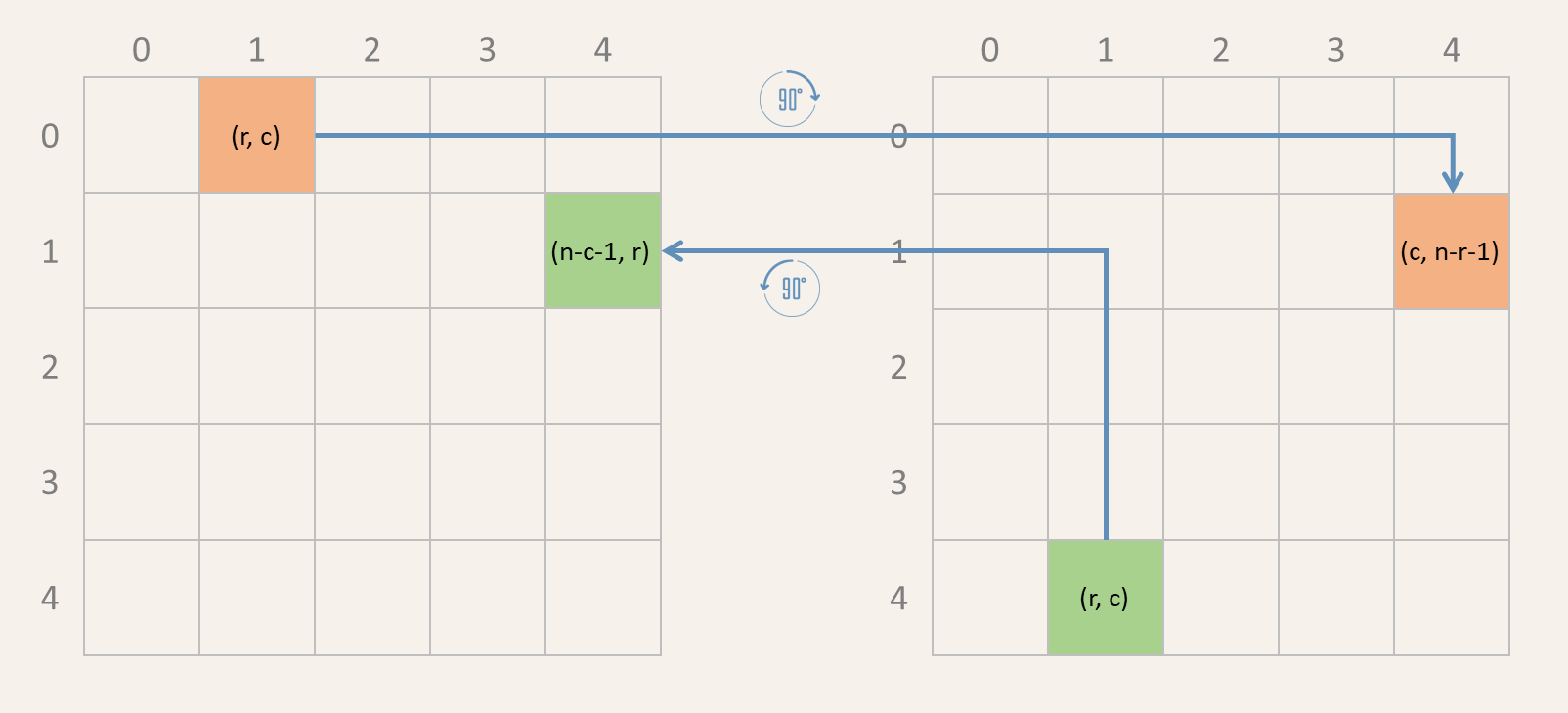
Positions of the cells if an $$n \times n$$ grid is rotated 90° clockwise/counterclockwise. If an $$n \times n$$ grid is rotated 90° counterclockwise, a cell at position $$(r, c)$$ ends up at position $$(n - c - 1, r)$$ (see green cell in the figure above).
If a grille (Grille) is passed to the built-in function str, a string representation (str) of its grid must be returned. Each row of the grid is on a separate line, cells with apertures are represented by the capital O, and cells without apertures are represented by a hash symbol (#).
Two grilles $$r$$ and $$s$$ (Grille) are equal (r == s) if they have the same number of rows/columns and if they can be rotated (multiples of 90°) such that all their apertures are at the same positions.
The addition (r + s) of two grilles $$r$$ and $$s$$ (Grille) produces a new grille $$t$$ (Grille) that looks as if both grilles $$r$$ and $$s$$ are put on top of each other. In other words, the apertures in $$t$$ are at positions where there are apertures in both $$r$$ and $$s$$. The addition is only defined for grilles $$r$$ and $$s$$ that have the same number of rows/columns. If this is not the case, an AssertionError must be raised with the message invalid operation.
Example
In the following interactive session we assume the text file message.txt2 to be located in the current directory.
>>> grille = Grille(5, [(0, 0), (1, 0), (1, 2), (1, 4), (3, 3), (4, 2)])
>>> grille.dimension
5
>>> grille.apertures
{(1, 2), (0, 0), (3, 3), (1, 4), (4, 2), (1, 0)}
>>> print(grille)
O####
O#O#O
#####
###O#
##O##
>>> grille.decode('message.txt3')
'East, '
>>> grille.rotate().apertures
{(3, 1), (2, 0), (2, 3), (4, 3), (0, 4), (0, 3)}
>>> print(grille)
###OO
#####
O##O#
#O###
###O#
>>> grille.decode('message.txt4')
'West, '
>>> grille.rotate().apertures
{(3, 2), (3, 0), (4, 4), (1, 1), (3, 4), (0, 2)}
>>> print(grille)
##O##
#O###
#####
O#O#O
####O
>>> grille.decode('message.txt5')
"home's"
>>> grille.rotate().apertures
{(0, 1), (1, 3), (2, 1), (4, 1), (2, 4), (4, 0)}
>>> print(grille)
#O###
###O#
#O##O
#####
OO###
>>> grille.decode('message.txt6')
' best.'
>>> grille.rotate(clockwise=False).apertures
{(3, 2), (3, 0), (4, 4), (1, 1), (3, 4), (0, 2)}
>>> print(grille)
##O##
#O###
#####
O#O#O
####O
>>> grille.decode('message.txt7')
"home's"
>>> grille1 = Grille(4, ((1, 3), (0, 0), (2, 3), (1, 1)))
>>> grille2 = Grille(4, {(2, 0), (1, 0), (3, 3), (2, 2)})
>>> grille3 = Grille(4, [(3, 0), (2, 3), (2, 0), (1, 1)])
>>> grille4 = Grille(5, ((1, 3), (0, 0), (2, 3), (1, 1)))
>>> grille1 == grille2
True
>>> grille1 == grille3
False
>>> grille1 == grille4
False
>>> grille5 = grille1 + grille3
>>> grille5.dimension
4
>>> grille5.apertures
{(2, 3), (1, 1)}
>>> print(grille5)
####
#O##
###O
####
>>> grille1 + grille4
Traceback (most recent call last):
AssertionError: invalid operation