X-ray diffraction is a tool used for identifying the atomic and molecular structure of a crystal, in which the crystalline atoms cause a beam of incident X-rays to diffract into many specific directions. By measuring the angles and intensities of these diffracted beams, a crystallographer can produce a three-dimensional picture of the density of electrons within the crystal. From this electron density, the mean positions of the atoms in the crystal can be determined, as well as their chemical bonds, their disorder and various other information.

$diffractiepatroon$

X-ray diffraction pattern formed when X-rays are focused on a crystalline material, in this case a protein. Each dot, called a reflection, forms from the coherent interference of scattered X-rays passing through the crystal.

Since many materials can form crystals — such as salts, metals, minerals, semiconductors, as well as various inorganic, organic and biological molecules — X-ray crystallography has been fundamental in the development of many scientific fields. In its first decades of use, this method determined the size of atoms, the lengths and types of chemical bonds, and the atomic-scale differences among various materials, especially minerals and alloys. The method also revealed the structure and function of many biological molecules, including vitamins, drugs, proteins and nucleic acids such as DNA. X-ray crystallography is still the chief method for characterizing the atomic structure of new materials and in discerning materials that appear similar by other experiments. X-ray crystal structures can also account for unusual electronic or elastic properties of a material, shed light on chemical interactions and processes, or serve as the basis for designing pharmaceuticals against diseases.

In a single-crystal X-ray diffraction measurement, a crystal is mounted on a goniometer. The goniometer is used to position the crystal at selected orientations. The crystal is bombarded with a finely focused monochromatic beam of X-rays, producing a diffraction pattern of regularly spaced spots known as reflections. The two-dimensional images taken at different rotations are converted into a three-dimensional model of the density of electrons within the crystal using the mathematical method of Fourier transforms, combined with chemical data known for the sample. Poor resolution (fuzziness) or even errors may result if the crystals are too small, or not uniform enough in their internal makeup.

Assignment

We simulate the scattering of X-rays that hits the atoms of a planar molecule, by subdividing the rectangular area occupied by the molecule into $$m$$ rows and $$n$$ columns ($$m, n \in \mathbb{N}_0$$). Each atom of the molecule occupies one of the cells of this rectangular grid, and cells never contain more than one atom.

We always bombard the molecules with X-rays that are oriented either to the north, east, south or west. Based on the way they deflect incoming X-rays, atoms fall in one of two categories. Atoms having forward deflection (left in figure below) bend X-rays directed towards the east to the north (and vice versa) and bend X-rays directed toward the south to the west. Atoms having backward deflection (right in figure below) bend X-rays directed toward the east to the south (and vice versa) and bend X-rays directed toward the north to the west (and vice versa).

Based on the way they deflect incoming X-rays, atoms fall in one of two categories. Atoms having forward deflection (left in figure below) bend X-rays directed towards the east to the north (and vice versa) and bend X-rays directed toward the south to the west. Atoms having backward deflection (right in figure below) bend X-rays directed toward the east to the south (and vice versa) and bend X-rays directed toward the north to the west (and vice versa).

In order to reference specific cells in the grid, we increasingly index the rows from north to south and the columns from west to east, with indexing always starting at zero (gray indices in the figure below). This allows us to represent the position of a cell in the grid as a tuple $$(r, c)$$, with $$r$$ the row index and $$c$$ the column index of the cell in the grid. We describe an X-ray which is incident on a molecule by the position of the cell where the beam is incident on the molecule, together with the direction to which the beam is directed. Your task is to determine for a given incident X-ray where and in which direction it will leave the molecule.

Below, we show some examples of X-rays that are incident on a molecule and are deflected by its molecules. The molecule to the left, for example has an atom with forward deflection at position (0, 2) and an atom with backward deflection at position (1, 1). As indicated by the green line, an X-ray directed to the south that hits the molecule at position (0, 1), is bent to the east by the atom at position (1, 1) and leaves the molecule in that direction at position (1, 4).

$diffraction$

Examples of X-rays that are incident on a molecule and are deflected by its molecules. The molecule to the left, for example has an atom with forward deflection at position (0, 2) and an atom with backward deflection at position (1, 1). As indicated by the green line, an X-ray directed to the south that hits the molecule at position (0, 1), is bent to the east by the atom at position (1, 1) and leaves the molecule in that direction at position (1, 4).

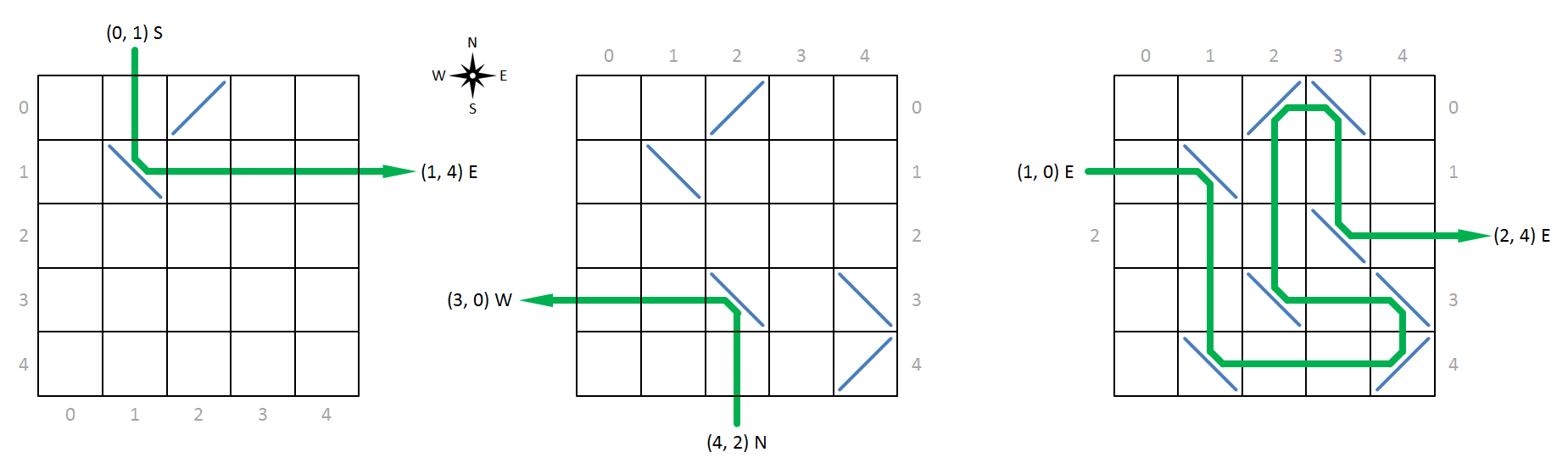
Your task is to write a class Molecule whose objects represent a planar molecule. The atoms of this molecule are organized in a rectangular $$m \times n$$ grid. Each cell of the grid may contain an atom having either forward or backward deflection, that behaves as described above. The class must support at least the following methods:

An initialization method that takes the number of rows $$m \in \mathbb{N_0}$$ and the number of columns $$n \in \mathbb{N_0}$$ of the rectangular grid. After initialization of an object, the grid does not contain any atoms yet, but during the lifetime of the object atoms having forward or backward deflection may be placed on the grid by calling the methods atom and atoms.
A method atom that can be used to place an atom on the grid. The method takes the position of the grid cell where the atom must be placed. In case the given position falls outside the grid or if this position is already occupied by another atom, the method must raise an AssertionError with the message invalid position. By default, the method places an atom having forward deflection. However, the method also has a second optional parameter forward that takes a Boolean value (default value: True). In case the value False is passed to this parameter, the method must place an atom having backward deflection.
A method atoms that can be used to place one or more atoms having the same type of deflection on the grid. The positions of these atoms must be passed to the method as a collection (a list, tuple or set). These positions must meet the same conditions as the position passed to the method atom. If this is not the case, the method must raise an AssertionError with the message invalid position. The method also has a second optional parameter forward that must be interpreted in the same way as for the method atom, and indicates the type of deflection of the atoms that must be placed on the grid.
A method __str__ that returns a string representation of the atoms that have been placed on the grid. This string representation contains $$m$$ lines that each contain $$n$$ space-separated symbols. The $$c$$-th symbol at the $$r$$-th line (lines and symbols are numbered starting from zero) indicates if the cell at position $$(r, c)$$ is occupied by an atom, and the type of deflection of this atom. Atoms having forward deflection are represented by a slash (/) and atoms having backward deflection are represented by a backward slag (\). Cells that are not occupied by an atom are indicated by a dot (.).
A method deflection that takes two arguments representing the coordinates of an incident X-ray: i) the position of the cell where the beam hits the molecule and ii) the direction in which the beam is directed. This direction is represented by a single letter: N for north, S for south, W for west and E for east. The method must return a list of positions in the grid that indicate the order of the cells visited by the X-ray as it passes through the molecule. In passing the molecule, the beam is deflected by its atoms as described in the introduction of this assignment.
A method diffraction that takes the same two arguments (with the same meaning) as the method deflection. The method must return a tuple containing two elements: i) the position where the beam leaves the molecule, and ii) the direction in which the beam leaves the molecule.

Note: Strings in Python use the backslash character as an escape symbol. Therefore, literal backslashes must be doubled in a string: '\\'.

Example

Note that a docstring is nothing but an ordinary string, which requires that each backslash that occurs literally in the docstring must be repeated twice. Click here to convert the following interactive session into a docstring.

>>> molecule = Molecule(5, 5)
>>> molecule.atom((0, 2))
>>> molecule.atom((1, 1), forward=False)
>>> print(molecule)
. . / . .
. \ . . .
. . . . .
. . . . .
. . . . .
>>> molecule.deflection((0, 1), 'S')
[(0, 1), (1, 1), (1, 2), (1, 3), (1, 4)]
>>> molecule.diffraction((0, 1), 'S')
((1, 4), 'E')

>>> molecule.atom((4, 4))
>>> molecule.atoms([(3, 2), (3, 4)], forward=False)
>>> print(molecule)
. . / . .
. \ . . .
. . . . .
. . \ . \
. . . . /
>>> molecule.deflection((4, 2), 'N')
[(4, 2), (3, 2), (3, 1), (3, 0)]
>>> molecule.diffraction((4, 2), 'N')
((3, 0), 'W')

>>> molecule.atoms({(0, 3), (2, 3), (4, 1)}, forward=False)
>>> print(molecule)
. . / \ .
. \ . . .
. . . \ .
. . \ . \
. \ . . /
>>> molecule.deflection((1, 0), 'E')
[(1, 0), (1, 1), (2, 1), (3, 1), (4, 1), (4, 2), (4, 3), (4, 4), (3, 4), (3, 3), (3, 2), (2, 2), (1, 2), (0, 2), (0, 3), (1, 3), (2, 3), (2, 4)]
>>> molecule.diffraction((1, 0), 'E')
((2, 4), 'E')

>>> molecule.atom((6, 6))
Traceback (most recent call last):
AssertionError: invalid position

>>> molecule.atom((1, 1))
Traceback (most recent call last):
AssertionError: invalid position