Given is a collection of tasks, each having a given start and end time. Two tasks are compatible if their execution intervals do not overlap. The aim is to select a subset of mutually compatible tasks that is as large as possible.

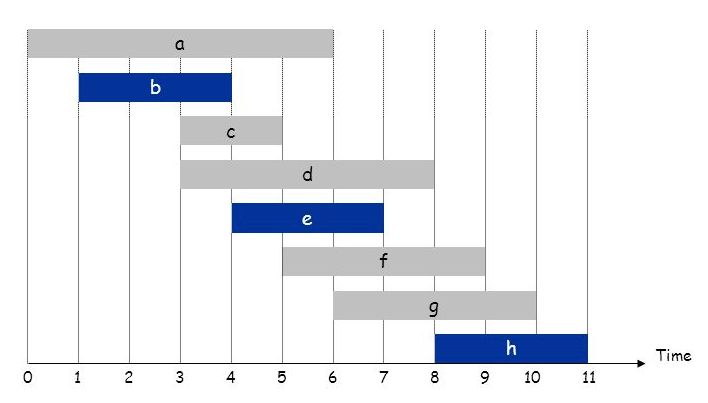
In the example below the optimal selection (b,e,h) has 3 tasks. All three are compatible with each other, while all remaining tasks are incompatible with at least one selected task, and there exists no larger valid selection.

Assignment

Write a Python-functie select which takes a list of tasks as parameter. The function returns the number of tasks selected, as well as a list of selected tasks.

Hint: look for a greedy approach that starts from an empty selection and then adds tasks one by one according to a given selection criterion. Try to find a selection criterion that guarantuees an optimal solution. If needed, experiment with different selection criteria, and try to understand why certain criteria do not always lead to the optimal solution.

Examples

>>> select([('a', 0, 6), ('b', 1, 4), ('c', 3, 5), ('d', 3, 8), ('e', 4, 7), ('f', 5, 9), ('g', 6, 10), ('h', 8, 11)])
(3, [('b', 1, 4), ('e', 4, 7), ('h', 8, 11)])

>>> select([('A', 1, 16), ('B', 24, 29), ('C', 8, 22), ('D', 4, 19), ('E', 30, 42), ('F', 35, 50), ('G', 8, 16), ('H', 4, 17), ('I', 9, 11)])
(3, [('B', 24, 29), ('E', 30, 42), ('I', 9, 11)])