Geohash is a geocoding system that encodes a geographic location into a short string of letters and digits. For example, geohash ezs42 encodes for an area around the coordinate with decimal longitude and latitude (-5.6, 42.6). Geohashes offer properties like arbitrary precision and the possibility of gradually removing characters from the end of the code to reduce its size (and gradually lose precision). As a consequence of the gradual precision degradation, nearby places will often (but not always) present similar prefixes. The longer a shared prefix is, the closer the two places are.
Using the area around coordinate (-5.6, 42.6) as an example — indicated by a red marker on the world map below — here is how it is encoded as a geohash. First we divide the world map with a vertical line into two halves and represent each half with a binary value: 0 (left half) and 1 (right half). Because the location is in the left half, the first bit of the geohash is a zero (0).
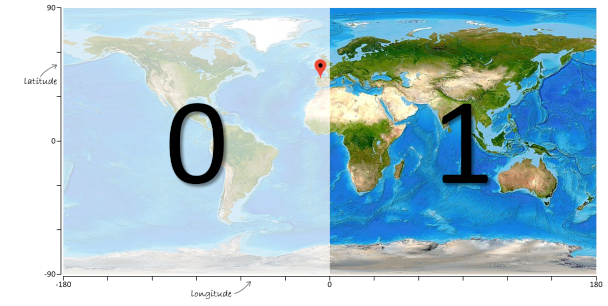
To improve the resolution of the location, we subdivide the remaining area again in two halves. But now we use a horizontal line for the division and also indicate each half with a binary value: 0 (bottom half) and 1 (top half). Because the location is in the top half, the second bit of the geohash is a one (1).

We then subdivide the remaining area in two halves, but again use a vertical line. Because the location is in the right half, the third bit of the geohash is also a one (1).

By iteratively subdividing the remaining area in two halves — alternating between vertical and horizontal subdivisions — we double the resolution of the geohash in each step, but also make the geohash one bit longer.
Assignment
Decode a given geohash into coordinate $$(\lambda, \varphi)$$ with $$\lambda, \varphi \in \mathbb{R}$$. The longitude $$\lambda$$ is in the interval $$[-180, 180]$$ and the latitude $$\varphi$$ in the interval $$[-90, 90]$$.
The decoding algorithm is outlined using the geohash ezs42 we recall from the introduction. The first step is to decode the geohash into its decimal value. Geohashes use 32 different characters in their symbol set: the digits 0–9 and the letters a–z, excluding a, i, l and o (no distinction is made between uppercase and lowercase letters). As a result, the geohash can be interpreted as a number in a base-32 numeral system. A number $$\left(c_{n}c_{n-1}\ldots c_{2}c_{1}c_{0}\right)_b$$ in a base-$$b$$ ($$b \in \mathbb{N}_0$$) numeral system can be converted into its decimal value using the following formula: \[ \sum_{i=0}^{n} \left(c_i\right)_{10} \times b^i \] where the notation $$\left(c_i\right)_{10}$$ is used for the decimal value of digit $$c_i$$ in the base-$$b$$ numeral system. The symbols $$\texttt{s}$$ in geohashes have the following decimal values:
| $$\texttt{s}$$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | b | c | d | e | f | g |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $$\texttt{t}_{10}$$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| $$\texttt{s}$$ | h | j | k | m | n | p | q | r | s | t | u | v | w | x | y | z |
| $$\texttt{t}_{10}$$ | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
The decimal value of geohash ezs42 with $$b = 32$$ is then computed as \[ \left(2 \times 32^{0}\right) + \left(4 \times 32^{1}\right) + \left(24 \times 32^{2}\right) + \left(31 \times 32^{3}\right) + \left(13 \times 32^{4}\right) = 14672002 \] This decimal value is then converted to a bitstring that represents the binary value of the geohash. In Python you can use the built-in function bin to convert a decimal value into its binary value.
>>> bin(14672002)
'0b110111111110000010000010'
When converting a decimal value into a bitstring, we might have to add leading zeros to the binary representation, because each symbol in a geohash encodes for 5 bits ($$2^5 = 32$$). For geohash ezs42 we obtain the 25-bit bitstring 0110111111110000010000010 (one leading zero).
If we now assume that counting starts at 0 in the left side, the even bits are taken for the longitude code (0111110000000), while the odd bits are taken for the latitude code (101111001001). Each of these bitstring can be interpreted as the instructions in a series of divisions, considering one bit at a time, again from the left to the right side. For the latitude value, the interval [-90, 90] is subdivided into two equal halves, producing two intervals: [-90, 0] and [0, 90]. Since the first bit is 1, the higher interval is chosen, and becomes the current interval. The procedure is repeated for all bits in the latitude bitstring. Finally, the latitude value is the center of the resulting interval. Longitudes are processed in an equivalent way, keeping in mind that the initial interval is [-180, 180].
For example, in the latitude bitstring 101111001001, the first bit is 1, so we know the latitude is somewhere between 0° and 90°. Without any more bits, we would guess the latitude was 45°, giving us an error of ±45°. Since more bits are available, we can continue with the next bit, and each subsequent bit halves this error. The table below shows the effect of each bit. At each stage, the relevant half of the interval is highlighted in green: a 0-bit selects the lower interval and a 1-bit selects the upper interval. The column "latitude" shows the estimation of the latitude as the mean value of the interval. Each subsequent bit makes this estimation more precise.
| position | bit | min | mid | max | latitude | maximum error |
|---|---|---|---|---|---|---|
| 0 | 1 | -90.000 | 0.000 | 90.000 | 45.000 | 45.000 |
| 1 | 0 | 0.000 | 45.000 | 90.000 | 22.500 | 22.500 |
| 2 | 1 | 0.000 | 22.500 | 45.000 | 33.750 | 11.250 |
| 3 | 1 | 22.500 | 33.750 | 45.000 | 39.375 | 5.625 |
| 4 | 1 | 33.750 | 39.375 | 45.000 | 42.188 | 2.813 |
| 5 | 1 | 39.375 | 42.188 | 45.000 | 43.594 | 1.406 |
| 6 | 0 | 42.188 | 43.594 | 45.000 | 42.891 | 0.703 |
| 7 | 0 | 42.188 | 42.891 | 43.594 | 42.539 | 0.352 |
| 8 | 1 | 42.188 | 42.539 | 42.891 | 42.715 | 0.176 |
| 9 | 0 | 42.539 | 42.715 | 42.891 | 42.627 | 0.088 |
| 10 | 0 | 42.539 | 42.627 | 42.715 | 42.583 | 0.044 |
| 11 | 1 | 42.539 | 42.583 | 42.627 | 42.605 | 0.022 |
The same procedure yields an estimation for the longitude (bitstring 0111110000000).
| position | bit | min | mid | max | longitude | maximum error |
|---|---|---|---|---|---|---|
| 0 | 0 | -180.000 | 0.000 | 180.000 | -90.000 | 90.000 |
| 1 | 1 | -180.000 | -90.000 | 0.000 | -45.000 | 45.000 |
| 2 | 1 | -90.000 | -45.000 | 0.000 | -22.500 | 22.500 |
| 3 | 1 | -45.000 | -22.500 | 0.000 | -11.250 | 11.250 |
| 4 | 1 | -22.5000 | -11.250 | 0.000 | -5.625 | 5.625 |
| 5 | 1 | -11.250 | -5.625 | 0.000 | -2.813 | 2.813 |
| 6 | 0 | -5.625 | -2.813 | 0.00 | -4.219 | 1.406 |
| 7 | 0 | -5.625 | -4.219 | -2.813 | -4.922 | 0.703 |
| 8 | 0 | -5.625 | -4.922 | -4.219 | -5.273 | 0.352 |
| 9 | 0 | -5.625 | -5.273 | -4.922 | -5.449 | 0.176 |
| 10 | 0 | -5.625 | -5.449 | -5.273 | -5.537 | 0.088 |
| 11 | 0 | -5.625 | -5.537 | -5.449 | -5.581 | 0.044 |
| 12 | 0 | -5.625 | -5.581 | -5.537 | -5.603 | 0.022 |
Your task:
-
Write a function geo2dec that takes a geohash (str) and returns its decimal value (int).
-
Write a function geo2bin that takes a geohash (str) and returns its bitstring representation (str).
-
Write a function unravel that takes a string (str) argument. If we number the characters in the given string from left to right starting at zero, the function must return a tuple (tuple) containing two strings (str), where the first string is composed from the characters at the even positions and the second string from the characters at the odd positions.
-
Write a function bin2coord that takes three arguments: i) a bitstring (str), ii) the lower limit $$l$$ (float) of an interval and iii) the upper limit $$u$$ (float) of the interval. The function must return a tuple (tuple) containing two numbers $$l', u' \in \mathbb{R}$$ (float) that describes the interval $$[l', u']$$ obtained by repeatedly halving the given interval $$[l, u]$$ according to the instructions in the given bitstring.
-
Write a function geo2coord that takes a geohash (str) and returns its corresponding coordinate $$(\lambda, \varphi)$$ as a tuple (tuple) containing numbers $$\lambda, \varphi \in \mathbb{R}$$ (float).
Example
>>> geo2dec('ezs42')
14672002
>>> geo2dec('DRUGGED')
13684424108
>>> geo2dec('ZUR1CH')
1068205424
>>> geo2bin('ezs42')
'0110111111110000010000010'
>>> geo2bin('DRUGGED')
'01100101111101001111011110110101100'
>>> geo2bin('ZUR1CH')
'111111101010111000010101110000'
>>> unravel('0110111111110000010000010')
('0111110000000', '101111001001')
>>> unravel('01100101111101001111011110110101100')
('010011001101110010', '10111110111101110')
>>> unravel('111111101010111000010101110000')
('111111110000100', '111000100111100')
>>> bin2coord('0111110000000', -180, 180)
(-5.625, -5.5810546875)
>>> bin2coord('101111001001', -90, 90)
(42.5830078125, 42.626953125)
>>> bin2coord('010011001101110010', -180, 180)
(-71.91375732421875, -71.91238403320312)
>>> bin2coord('10111110111101110', -90, 90)
(44.27215576171875, 44.273529052734375)
>>> bin2coord('111111110000100', -180, 180)
(178.6376953125, 178.648681640625)
>>> bin2coord('111000100111100', -90, 90)
(69.23583984375, 69.2413330078125)
>>> geo2coord('ezs42')
(-5.60302734375, 42.60498046875)
>>> geo2coord('DRUGGED')
(-71.91307067871094, 44.27284240722656)
>>> geo2coord('ZUR1CH')
(178.6431884765625, 69.23858642578125)