What's so special about the number 105263157894736842? This number doubles if you move the rightmost digit to the front of the number. In addition, this is the smallest natural number that has this property.

In general, a positive natural number that can be multiplied by $$n$$ by moving the rightmost digit to the front of the number is called an $$n$$-parasitic number. Here $$n$$ is itself a single-digit positive natural number. For example \[ 4 \times 128205 = 512820 \] so 128205 is a 4-parasitic number. Natural numbers with leading zeros are not allowed. So even though \[ 4 \times 025641 = 102564 \] the number 025641 is not 4-parasitic.
The corkscrew method is a technique that can be used to derive an $$n$$-parasitic number the ends with a given digit $$k$$, which should be chosen such that $$k \geq n$$. The method generates the $$n$$-parasitic number one digit at a time, starting with rightmost digit. In other words, the $$n$$-parasitic number is constructed right to left. This is illustrated below for $$n = 4$$ and $$k = 7$$.
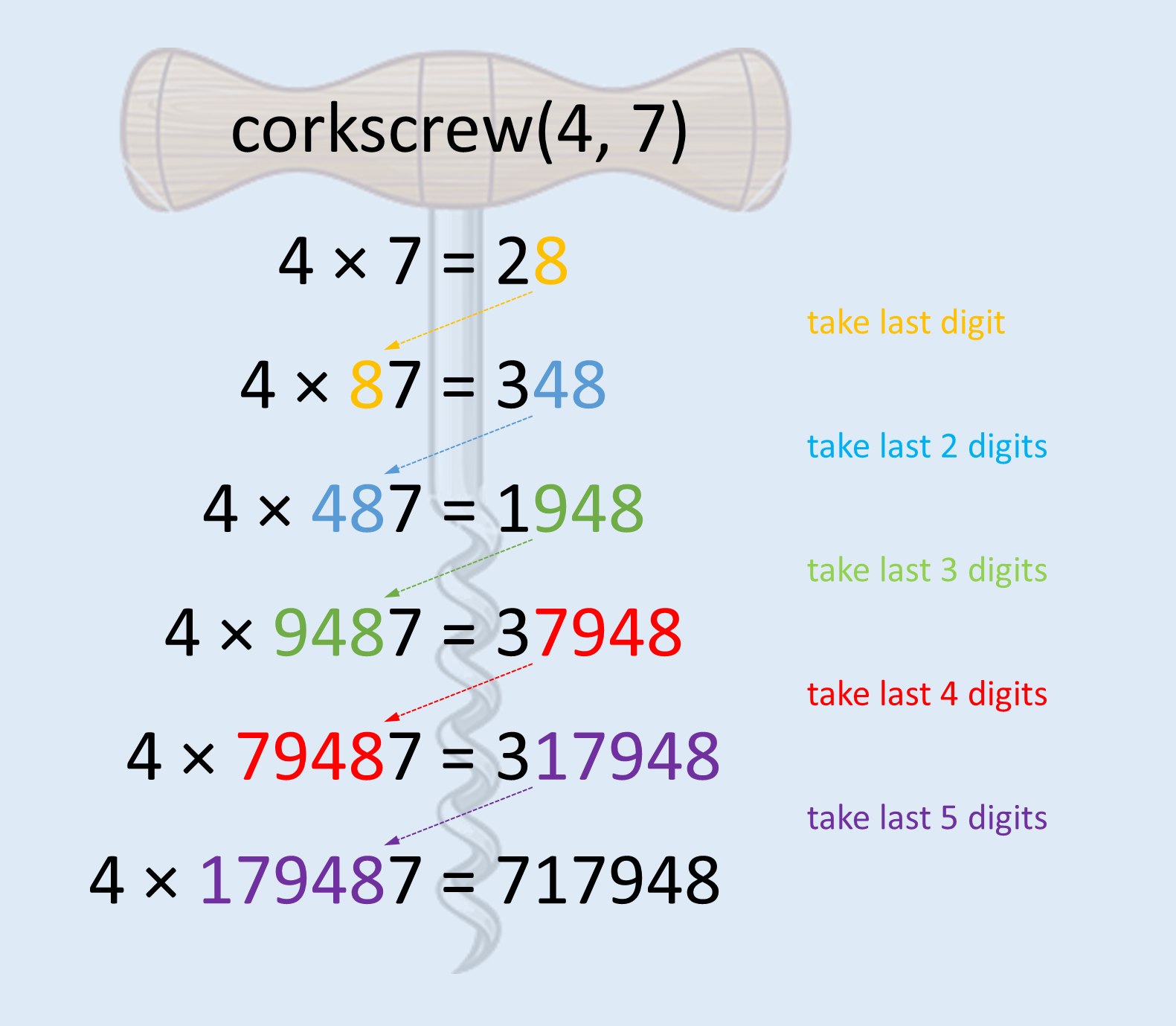
The method thus progresses by gradually taking one more digit from the end of the result of the multiplication, appending the digit $$k$$ at the end of this sequence of digits, and multiplying the resulting number by $$n$$. The first time we compute $$n \times k$$, take the last digit of the result, append the digit $$k$$ and multiply that number by $$n$$. Then we take the last two digits from the result of the multiplication, append the digit $$k$$ and multiply this number by $$n$$. We keep on repeating this procedure until the multiplication results in a number that is the same as the number that was multiplied by $$n$$, but with the rightmost digit moved to the front.
Assignment
The operation where the leftmost digit is moved to the end of a natural number is called a left rotation. The operation where the rightmost digit is moved to the front of a natural number is called a right rotation. In both cases, any leading zeros that might pop up are removed. Your task:
-
Write a function rotate_left that takes a natural number. The function must return the natural number that results after applying a left rotation on the given natural number.
-
Write a function rotate_right that takes a natural number. The function must return the natural number that results after applying a right rotation on the given natural number.
-
Write a function parasitic that takes a natural number. In case the given natural number is $$n$$-parasitic, the function must return the value $$n$$. Otherwise, the function must return the value 0.
-
Write a function corkscrew that takes two natural numbers $$n$$ and $$k$$. The function must return the $$n$$-parasitic number that ends with the digit $$k$$ that results from applying the corkscrew method. The function may assume that $$n$$ and $$k$$ are both single-digit natural numbers, with $$k \geq n$$.
Example
>>> rotate_left(717948)
179487
>>> rotate_left(142857)
428571
>>> rotate_left(105263157894736842)
52631578947368421
>>> rotate_right(179487)
717948
>>> rotate_right(428571)
142857
>>> rotate_right(52631578947368421)
15263157894736842
>>> parasitic(179487)
4
>>> parasitic(142857)
5
>>> parasitic(105263157894736842)
2
>>> parasitic(1234)
0
>>> corkscrew(4, 7)
179487
>>> corkscrew(5, 7)
142857
>>> corkscrew(2, 2)
105263157894736842
For debugging purposes, the figures below apply the corkscrew method for the two other examples in the above sample session.

