Chaos theory1 is a field of study in mathematics, with applications in several disciplines including meteorology, physics, engineering, economics and biology. It studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the butterfly effect2.
Small differences in initial conditions — such as those due to rounding errors in numerical computation — yield widely diverging outcomes for such dynamical systems, rendering long-term prediction impossible in general. This happens even though these systems are deterministic, meaning that their future behavior is fully determined by their initial conditions, with no random elements involved. In other words, the deterministic nature of these systems does not make them predictable.
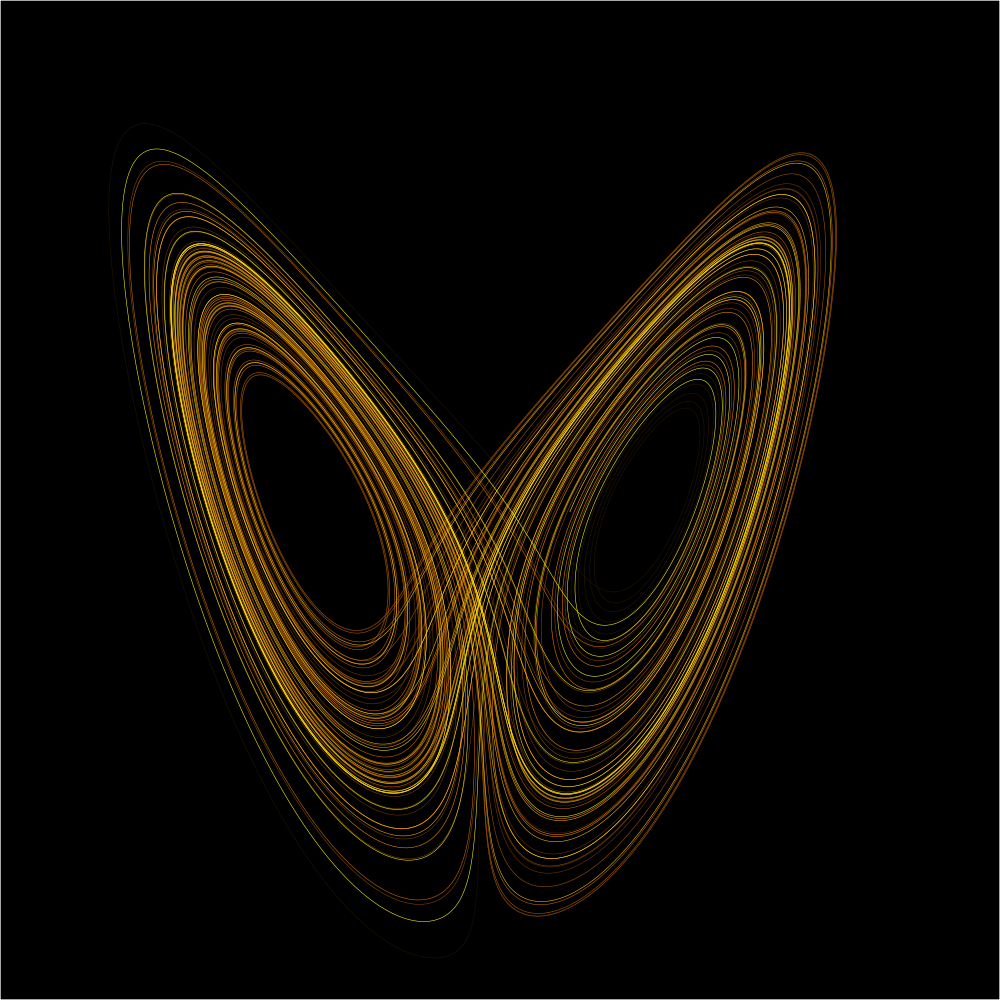
This behavior is known as deterministic chaos, or simply chaos. The theory was summarized by Edward Lorenz3 as:
The fluttering of a butterfly's wing in Rio de Janeiro, amplified by atmospheric currents, could cause a tornado in Texas two weeks later.
— Edward Lorenz
Assignment
The following simple model for population growth might be applied to study fish in a pond, bacteria in a test tube, or any of a host of similar situations. We suppose that the population ranges from 0 (extinct) to 1 (maximum population that can be sustained).
If the population at time $$t_i$$ is $$d$$, then we suppose the population at time $$t_{i+1}$$ to be $$rd(1-d)$$, where the argument $$r$$ — known as the fecundity parameter — controls the growth rate.
Input
Three lines containing i) the initial density $$d \in \mathbb{R}$$ of a population, ii) the fecundicity parameter $$r \in \mathbb{R}$$, and iii) the number of time steps $$s \in \mathbb{N_0}$$ we want to simulate the population density (including time point $$t_0$$).
Output
$$s$$ lines containing the population density at time points $$t_0, t_1, \ldots, t_{s-1}$$.
Example
If $$r$$ has a value of around $$2$$, the population density will approach $$1 - \frac{1}{r}$$ as time progresses.
Input:
0.1
1.9
6Output:
0.1
0.171
0.26934210000000003
0.373914173018421
0.44479449204530547
0.4692094685937818Example
If $$r = 3$$ the population density will converge to a state where the population density alternates between two values.
Input:
0.1
3
12Output:
0.1
0.2700000000000001
0.5913000000000002
0.7249929299999999
0.5981345443500454
0.7211088336156269
0.603332651091411
0.7179670896552621
0.6074710434816448
0.7153499244388992
0.6108732301324811
0.7131213805199696Example
If $$r \geq 4$$ the model will behave in a chaotic way. This means that the results can change drastically when the initial conditions are slightly perturbed. See the difference in behavior between this example and the next example.
Input:
0.1
4
60Output:
0.1
0.36000000000000004
0.9216
... (54 lines) ...
0.977464119602946
0.08811205796713474
0.32139329283172413Example
A difference of $$0.00000000001$$ in the initial population density causes a huge difference in the population density at time point $$t_{59}$$. This is chaotic behaviour, showing that it is hard to predict population densities, because tiny pertubations cause large differences in the long run.
Input:
0.10000000001
4
60Output:
0.10000000001
0.36000000003200006
0.9216000000358401
... (54 lines) ...
0.830632498181969
0.5627286045838009
0.9842604886678766Epilogue
You may get different results for the final two examples. Different programming languages or computing environments can use different ways to round floating point numbers. These tiny differences cause huge differences in processing the floating point numbers due to the chaotic nature of the model.
As an additional exercise, you can study the difference between using the formula $$rd(1-d)$$ and the identical formula (mathematically speaking) $$rd - rd^2$$. Implementations relying on either of these formulas will result in different rounding errors.
The meteorologist Edward Lorenz4 also noticed these effects caused by rounding errors when studying his model of atmospheric convection5. His studies of these effects made him one of the pioneers of chaos theory6.
Epilogue: the earthquake rose
When a magnitude 6.8 earthquake shook Olympia, Washington, USA on February 28, 2001, shop owner Jason Ward discovered that a sand-tracing pendulum had recorded the vibrations in the image below.

Seismologists say that the "flower" at the center reflects the higher-frequency waves that arrived first. The outer, larger-amplitude oscillations record the lower-frequency waves that arrived later. Norman MacLeod — president of Gaelic Wolf Consulting in Port Townsend — told ABC News7
You never think about an earthquake as being artistic — it's violent and destructive. But in the middle of all that chaos, this fine, delicate artwork was created.