A place on Earth is indicated with spherical co-ordinates consisting of a pair of co-ordinates that respectively indicate the longitude an latitude. The latitude is the angle made by the joining line between that place and the centre of the Earth and the surface of the equator, and varies from -90° to 90° (both enclosed). The longitude is the angle between the meridian surface of Greenwich and the meridian surface of the measuring point and varies from -180° to 180° (half-open interval in which -180° is excluded).
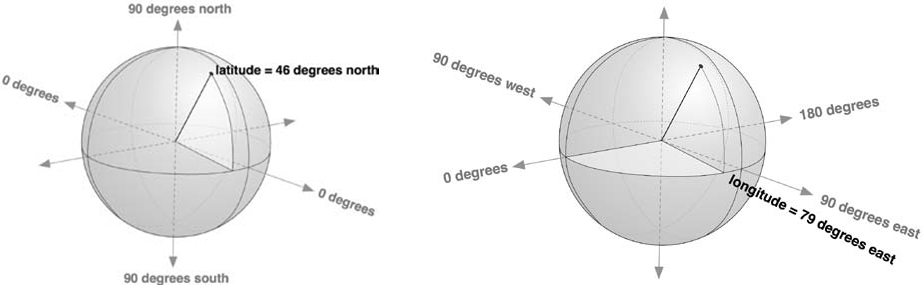
In the most simple decimal notation a co-ordinate is given as a real number that indicates the number of degrees. Negative numbers indicate southern latitude or western longitude and the positive cases for northern latitude and the eastern longitude. In GMS notation a grade (*) is further divided in 60 minutes ('), and a minute is further divided in 60 seconds ("). To a latitude $$b$$ a s (southern latitude) is added if it is situated on the Southern Hemisphere ($$?90° \leq b \leq 0°$$), and an N (northern latitude) is added if it is situated on the Northern Hemisphere ($$0° < b \leq 90°$$). To a longitude $$l$$ a W (western longitude) is added if it is situated west of the prime meridian. If it is situated east of the prime meridian ($$0° < l \leq 180°$$), an e (eastern longitude) is added.
Assignment
Write a function degrees2GMS that converts a given co-ordinate $$g$$ ($$g \in \mathbb{R}$$, with $$g \geq 0$$) in decimal notation to the corresponding GMS notation. The co-ordinate $$g$$ should be passed to the function as a real number. The function should print a string of the format G*M'S" as a result, as a representation of the co-ordinate in GMS notation. The values $$G$$, $$M$$ and $$S$$ are calculated as follows:
the number of degrees $$G$$ is the absolute value for the decimal point of $$g$$: $$87,728055 = 87\ \text{graden}$$
multiply the part after the decimal point of $$G$$ by 60; the number of minutes $$M$$ is the part before the decimal point of the value in the outcome: $$0,728055 \times 60 = 43,6833 = 43\ \text{minuten}$$
multiply the part after the decimal point by 60; the seconds $$S$$ are calculated by rounding off this number to the nearest integer: $$0,6833 \times 60 = 40,998 = 41\ \text{seconden}$$
the final result is the string 87*43'41"
Use the function degrees2GMS to write a function coord2GMS. Two real arguments should be passed to this function, that respectively represent the latitude and the longitude in decimal notation. As a result, the function must print a string that shows the location by giving both co-ordinates in GMS notation. For example, the function should print a string 40*26'46"N 79*56'56"W for the values 40,446195 and -79,948862. If an invalid longitude or latitude is given to the function, the string must print invalid as a result.
Example
>>> print(degrees2GMS(40.446195))
40*26'46"
>>> print(degrees2GMS(79.948862))
79*56'56"
>>> print(coord2GMS(40.446195, -79.948862))
40*26'46"N 79*56'56"W
>>> print(coord2GMS(-83.827439, -180.0))
invalid