In de figuur zie je het fictieve wegennet van Vlaanderen, anno 1961.
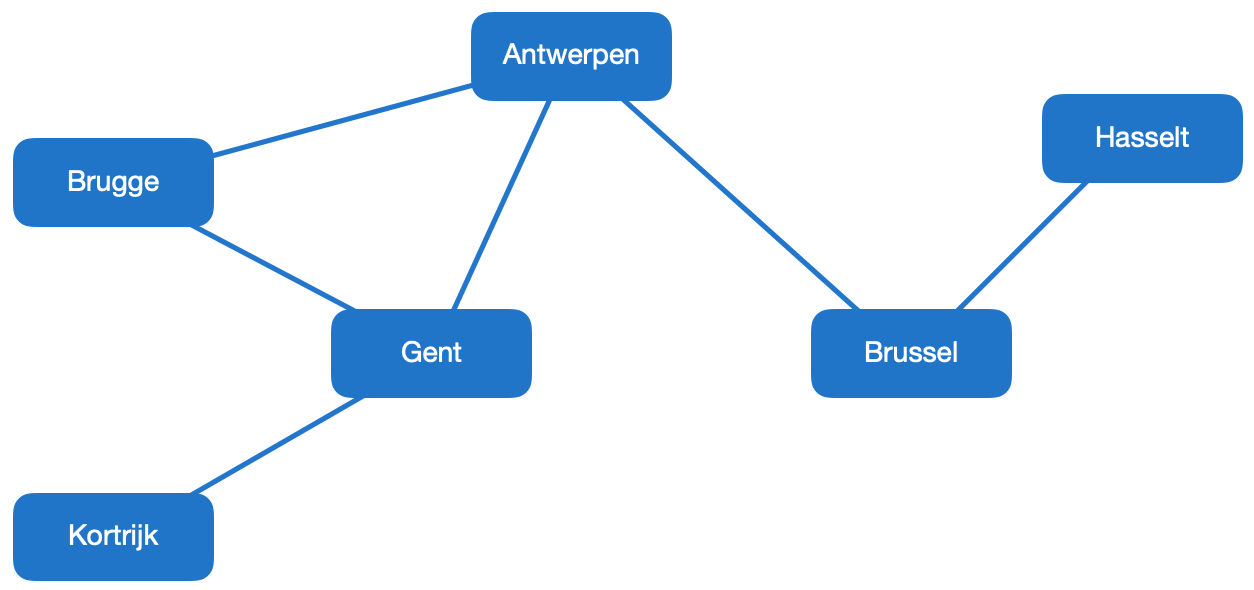
De kaart stellen we voor door een dictionary. De keys van de dictionary zijn de steden op de kaart. De value die hoort bij een key is een set met alle steden die je vanuit de gegeven stad rechtstreeks kan bereiken.
{
'Brugge': {'Antwerpen', 'Gent'},
'Kortrijk': {'Gent'},
'Gent': {'Antwerpen', 'Kortrijk', 'Brugge'},
'Antwerpen': {'Brussel', 'Brugge', 'Gent'},
'Brussel': {'Antwerpen', 'Hasselt'},
'Hasselt': {'Brussel'}
}
Twee voorbeelden:
- Vanuit Gent bereik je Antwerpen, Kortrijk en Brugge rechtstreeks.
- Vanuit Kortrijk bereik je enkel Gent rechtstreeks.
Je mag er steeds vanuit gaan dat wanneer je stad X rechtstreeks kan bereiken vanuit stad Y, het omgekeerde ook geldig is en dat de dictionary voldoet aan dit principe. Er is ook nooit een stad opgenomen die met geen enkele andere stad verbonden is.
Opgave
Programmeer volgende vier functies:
- bestaat_weg: de derde parameter is de dictionary met de wegenkaart. De eerste en tweede parameter zijn twee steden. Indien beide steden rechtstreeks verbonden zijn door een weg, dan geeft de functie True terug. In het andere geval False.
- geen_dubbelburen: de derde parameter is de dictionary met de wegenkaart. De eerste en tweede parameter zijn twee steden A en B. De functie geeft een set steden terug die rechtstreeks verbonden zijn met stad A of met stad B maar niet met beide steden A en B tegelijkerijd. De steden A en B zijn nooit deel van de oplossing.
- bereikbaarheid_meest_afgelegen_stad: berekent met hoeveel steden de meest onbereikbare stad of steden rechtstreeks verbonden zijn. De enige parameter is de dictionary met de wegenkaart.
- bestaat_route: de tweede parameter is de dictionary met de wegenkaart. De eerste parameter is een lijst van steden. De functie geeft True terug indien alle opeenvolgende steden in de lijst rechtstreeks verbonden zijn met een weg. In het andere geval laat je False teruggeven.
Voorbeeld
>>> kaart = {'Brugge': {'Gent', 'Antwerpen'}, 'Kortrijk': {'Gent'}, 'Gent': {'Antwerpen', 'Kortrijk', 'Brugge'}, 'Antwerpen': {'Gent', 'Brussel', 'Brugge'}, 'Brussel': {'Hasselt', 'Antwerpen'}, 'Hasselt': {'Brussel'}}
>>> bestaat_weg('Brussel', 'Hasselt', kaart)
True
>>> bestaat_weg('Antwerpen', 'Kortrijk', kaart)
False
>>> geen_dubbelburen('Brussel', 'Hasselt', kaart)
{'Antwerpen'}
>>> geen_dubbelburen('Antwerpen', 'Kortrijk', kaart)
{'Brussel', 'Brugge'}
>>> bereikbaarheid_meest_afgelegen_stad(kaart)
1
>>> bestaat_route(['Hasselt', 'Brussel', 'Antwerpen', 'Brugge', 'Gent', 'Kortrijk'], kaart)
True
>>> bestaat_route(['Brugge', 'Hasselt', 'Brussel'], kaart)
False