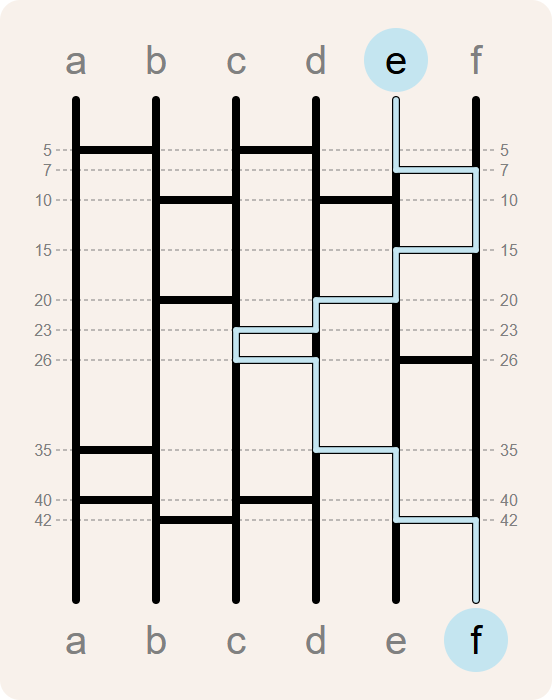
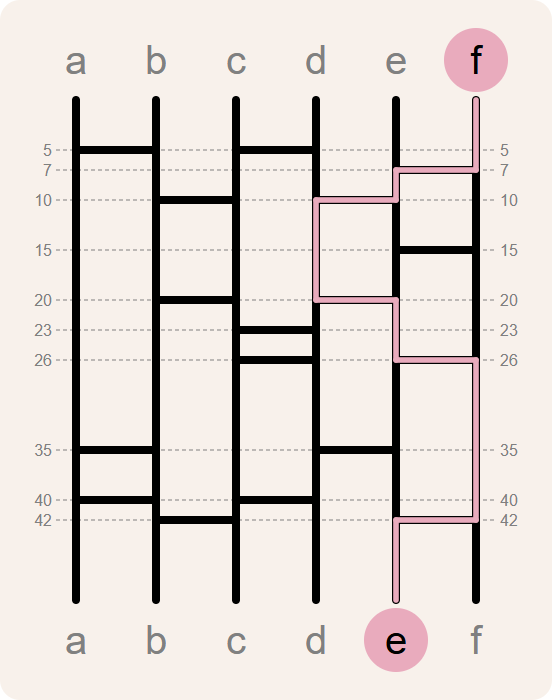
Ghost leg is a method of establishing random pairings between any two groups of equal size. For example, it might be used to assign $$n$$ chores randomly to a group of $$n$$ people. In Japanese the method is known as amidakuji.

At first, a diagram is drawn consisting of $$n$$ vertical lines. Such a vertical line is called a stem. Then a random number of "legs" are added at random positions in the diagram. A leg is a horizontal line that connects two adjacent stems. It is not allowed for a stem to both have a leg to the left and a leg to the right at the same height.

Then the middle part of the diagram is covered up to conceal the legs. Only the top and bottom segments of each stem are visible, so one can't tell which top segment leads to which bottom segment. Each task is assigned to the bottom segment of a stem, and everyone chooses a top segment of a stem as their starting position (no two people at the same stem).

Now the ghost legs are revealed and each person can follow a path from the top of the diagram to the bottom of the diagram. In doing so, they must follow each leg they encounter, jump to the adjacent stem and continue downward. When a person reaches the bottom of the diagram, it establishes a link between the person and the chore found there.

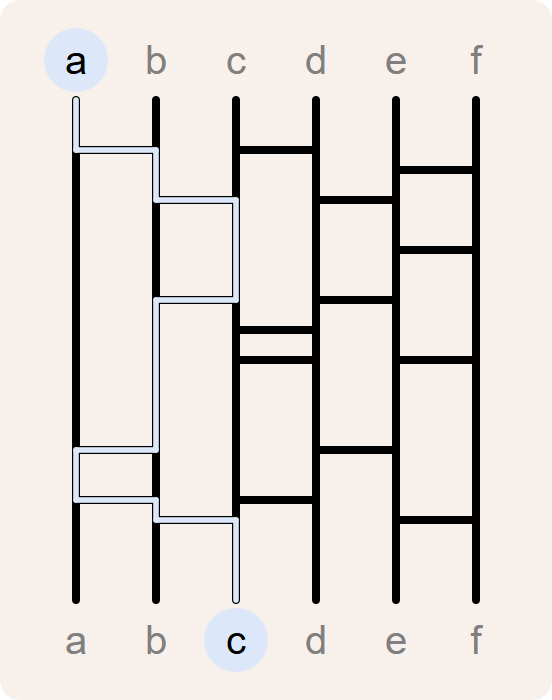
The benefit of this method is that it works for groups of any size, reliably establishing a 1:1 correspondence between their items. And it works no matter how many legs are added.

Assignment

The diagram of an amidakuji is described in a text file. Each stem is labelled with a unique letter. The top of the diagram is at distance 0 and distances increase as we move further down the diagram. Each line of the text file describes a leg of the amidakuji using three space-separated fields. The first two fields contain the labels of the adjacent stems connected by the leg. The third field contains the distance from the leg to the top of the diagram. Distances are always expressed as natural numbers. If these are the distances of the legs in the amidakuji we used as an example

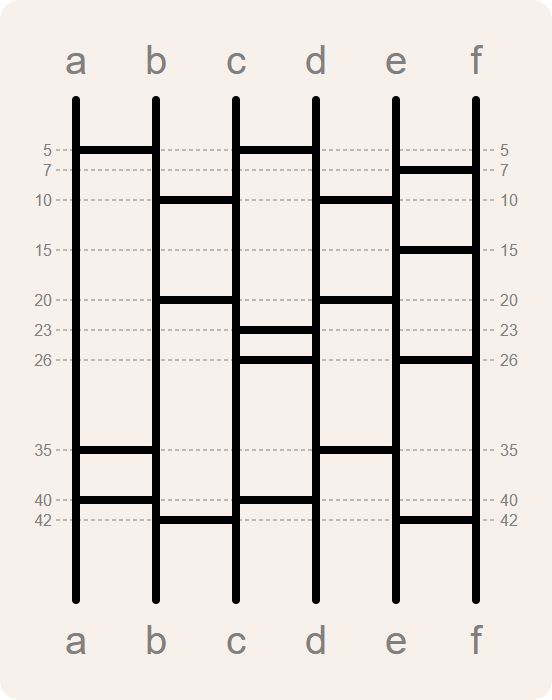
then the diagram can be described by this text file (amidakuji.txt¹)

a b 5
c d 5
e f 7
b c 10
d e 10
e f 15
b c 20
d e 20
c d 23
c d 26
e f 26
a b 35
d e 35
a b 40
c d 40
b c 42
e f 42

Your task:

• Write a function read_branches that takes the location (str) of a text file describing the diagram of an amidakuji. If the diagram contains a stem that has both a leg to the left and a leg to the right at the same height, an AssertionError must be raised with the message invalid amidakuji. Otherwise, the dictionary representation of the amidakuji must be returned. This is a dictionary (dict) whose keys are the labels (str) of the stems of the amidakuji. The dictionary must map the label (str) of a stem onto a dictionary (dict) that maps the height (int) of each leg that branches of from the stem onto the label (str) of the adjacent stem to which the leg leads.

• Write a function path that takes two arguments: i) the label $$s$$ (str) of a stem and ii) the dictionary representation (dict) of an amidakuji. If the amidakuji has no stem with label $$s$$, an AssertionError must be raised with the message invalid stem. Otherwise, the function must return the path that starts from stem $$s$$ at the top of the diagram and runs through the amidakuji to the bottom of the diagram. The path is described as a list of successive jumps to adjacent stems along the path. A jump is described as a tuple with two elements: i) the distance (int) where the path jumps to an adjacent stem and ii) the label of the adjacent stem the path jumps to. The path starts by jumping to stem $$s$$ at distance 0. The function must not change the dictionary representation (dict) of the amidakuji.

• Write a function amidakuji that takes the dictionary representation (dict) of an amidakuji. The function must return a dictionary (dict) that maps the label (str) of each stem in the amidakuji onto the label (str) of the end point (also a stem) of the path through the amidakuji that starts from that stem at the top of the diagram. The function must not change the dictionary representation (dict) of the amidakuji.

Example

In the following interactive session we assume the current directory contains the text file amidakuji.txt². It describes the diagram of the amidakuji we used as an example in this assignment.

>>> branches = read_branches('amidakuji.txt3')
>>> branches['a']
{5: 'b', 35: 'b', 40: 'b'}
>>> branches['b']
{5: 'a', 10: 'c', 20: 'c', 35: 'a', 40: 'a', 42: 'c'}
>>> branches['c']
{5: 'd', 10: 'b', 20: 'b', 23: 'd', 26: 'd', 40: 'd', 42: 'b'}
>>> branches['d']
{5: 'c', 10: 'e', 20: 'e', 23: 'c', 26: 'c', 35: 'e', 40: 'c'}
>>> branches['e']
{7: 'f', 10: 'd', 15: 'f', 20: 'd', 26: 'f', 35: 'd', 42: 'f'}
>>> branches['f']
{7: 'e', 15: 'e', 26: 'e', 42: 'e'}

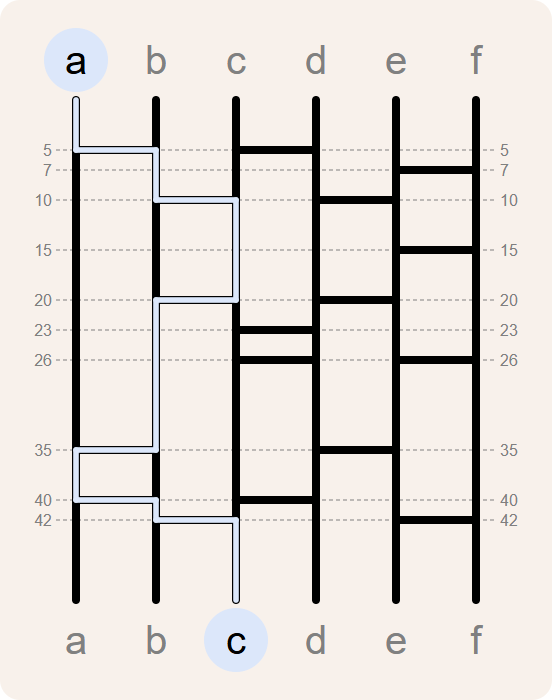
>>> path('a', branches)
[(0, 'a'), (5, 'b'), (10, 'c'), (20, 'b'), (35, 'a'), (40, 'b'), (42, 'c')]
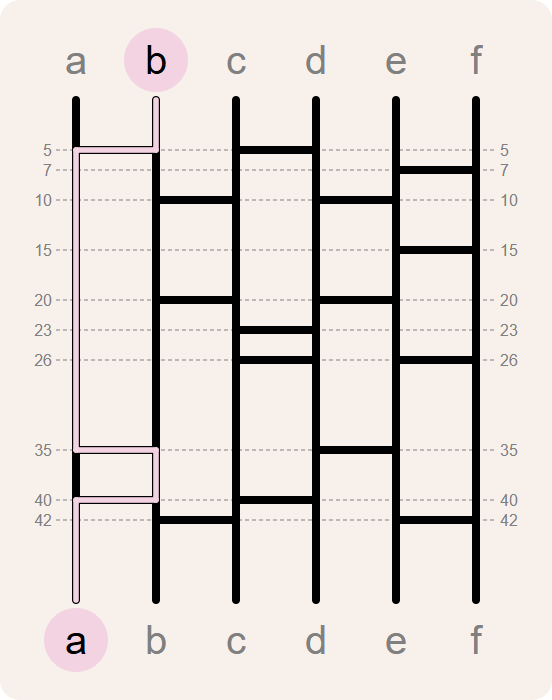
>>> path('b', branches)
[(0, 'b'), (5, 'a'), (35, 'b'), (40, 'a')]
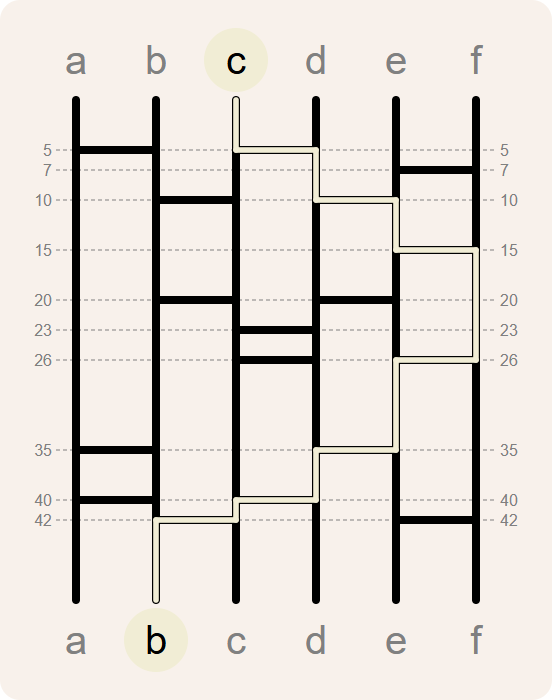
>>> path('c', branches)
[(0, 'c'), (5, 'd'), (10, 'e'), (15, 'f'), (26, 'e'), (35, 'd'), (40, 'c'), (42, 'b')]
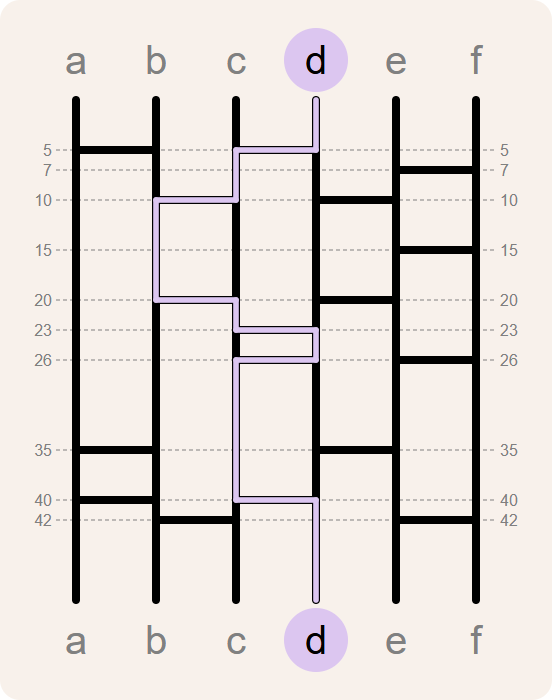
>>> path('d', branches)
[(0, 'd'), (5, 'c'), (10, 'b'), (20, 'c'), (23, 'd'), (26, 'c'), (40, 'd')]
>>> path('e', branches)
[(0, 'e'), (7, 'f'), (15, 'e'), (20, 'd'), (23, 'c'), (26, 'd'), (35, 'e'), (42, 'f')]
>>> path('f', branches)
[(0, 'f'), (7, 'e'), (10, 'd'), (20, 'e'), (26, 'f'), (42, 'e')]

>>> amidakuji(branches)
{'a': 'c', 'b': 'a', 'c': 'b', 'd': 'd', 'e': 'f', 'f': 'e'}

These are the paths through the amidakuji that start from the different stems at the top of the diagram.