Adjacent numbers is a brain teaser that starts with an empty rectangular $$m \times n$$ grid with $$m$$ rows and $$n$$ columns. The goal of the puzzle is to fill the cells of the grid with numbers 1 through 9, so that the total sum of all numbers in the grid is as large as possible. The rules to fill the cells of the grid are as follows:

• all cells must be filled with a number between 1 and 9

• the number 1 can fill any cell in the grid

• the number 2 can fill any cell, provided it is adjacent to a cell containing the number 1

• the number 3 can fill any cell, provided it is adjacent to cells containing the numbers 2 and 1

• …

• the number 9 can fill any cell, provided it is adjacent to cells containing the numbers 8, 7, 6, 5, 4, 3, 2 and 1

• adjacent cells are horizontal, vertical or diagonal neighbours of a cell (each cell has at most 8 adjacent cells; they are in a move's reach of a chess King)

• there are no limits on how many times you can use each number between 1 and 9 — except to comply with the above rules — and you are not obliged to use any number

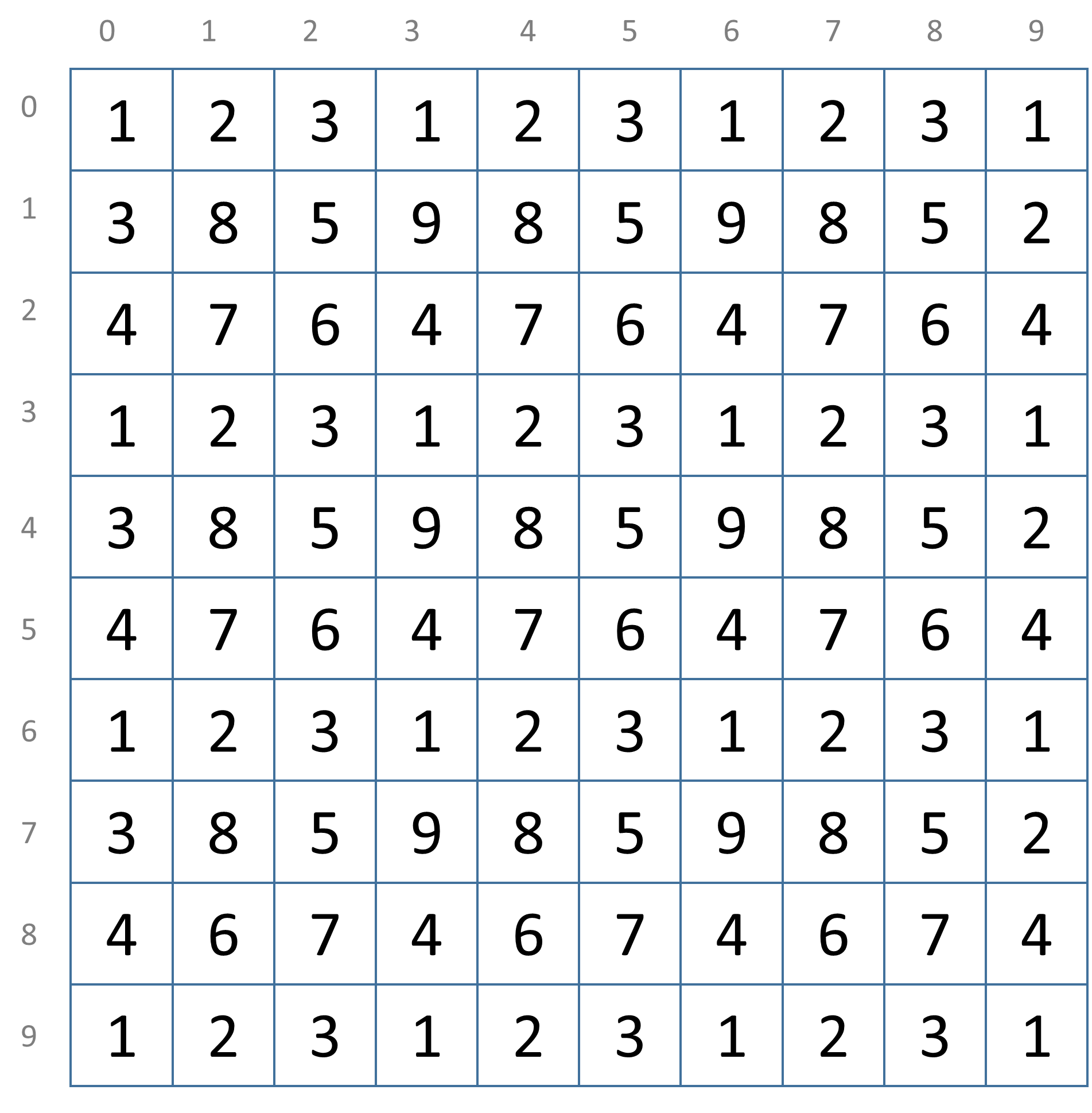
Multiple optimal solutions (solutions with the same maximal total sum) can usually exist for a rectangular grid of a given size. The following grid shows a valid solution with total sum 427. This is the most optimal solution that is currently known for a $$10 \times 10$$ grid.

Assignment

Finding optimal solutions for a rectangular grid of a given size is a very hard problem. For this assignment, you are only asked to check whether a rectangular grid filled with integers is a valid solution for the adjacent numbers puzzle. In other words, you have to check if the grid complies to the rules that were outlined in the introduction. We will use two different ways to represent a rectangular $$m \times n$$ grid filled with numbers between 1 and 9.

The grid can be represented as a string that lists the order of the digits if all cells of the grid are visited from left to right and from top to bottom. Together with this string, the number of columns must also be given to unambiguously describe the size of the grid. Of course, the number of digits in the string must be a multiple of the number of columns in the grid. This is called the string representation of the grid.

The grid can also be represented as a list containing the $$m$$ rows of the grid, listed from top to bottom. Each row is itself represented as a list containing the $$n$$ integers on that row, listed from left to right. This is called the list representation of the grid.

The rows of the grid are indexed top to bottom, starting from zero. The columns of the grid are indexed left to right, starting from zero. Your task:

• Write a function listRepresentation that takes a sequence of digits (a string) and a number of columns (an integer). Both arguments correspond to the string representation of a rectangular grid filled with numbers between 1 and 9. The function must return the list representation of the given grid. In case the two given arguments are no valid string representation of a rectangular grid filled with numbers between 1 and 9, the function must raise an AssertionError with the message invalid string representation.

• Write a function neighbours that takes three arguments: i) a row index (integer), ii) a column index (integer) and iii) the list representation of a rectangular grid filled with numbers between 1 and 9. The function must return a set containing the digits in all adjacent cells of the cell at the given position in the grid. In case the given row and column index do not represent a position inside the grid, the function must raise an AssertionError with the message invalid position.

• Write a function isAdjacent that takes a sequence of digits (a string) and a number of columns (an integer). Both arguments correspond to the string representation of a rectangular grid filled with numbers between 1 and 9. The function must return a Boolean value that indicates whether or not the given grid is a valid solution for the adjacent number puzzle, and thus complies to the rules outlined in the introduction. In case the two given arguments are no valid string representation of a rectangular grid filled with numbers between 1 and 9, the function must raise an AssertionError with the message invalid string representation.

Example

>>> listRepresentation('111222333', 3)
[[1, 1, 1], [2, 2, 2], [3, 3, 3]]
>>> listRepresentation('123321123', 3)
[[1, 2, 3], [3, 2, 1], [1, 2, 3]]
>>> listRepresentation('424313424', 3)
[[4, 2, 4], [3, 1, 3], [4, 2, 4]]
>>> listRepresentation('1541253263631421', 4)
[[1, 5, 4, 1], [2, 5, 3, 2], [6, 3, 6, 3], [1, 4, 2, 1]]
>>> listRepresentation('1541253263631421', 5)
Traceback (most recent call last):
AssertionError: invalid string representation

>>> grid = [[1, 5, 4, 1], [2, 5, 3, 2], [6, 3, 6, 3], [1, 4, 2, 1]]
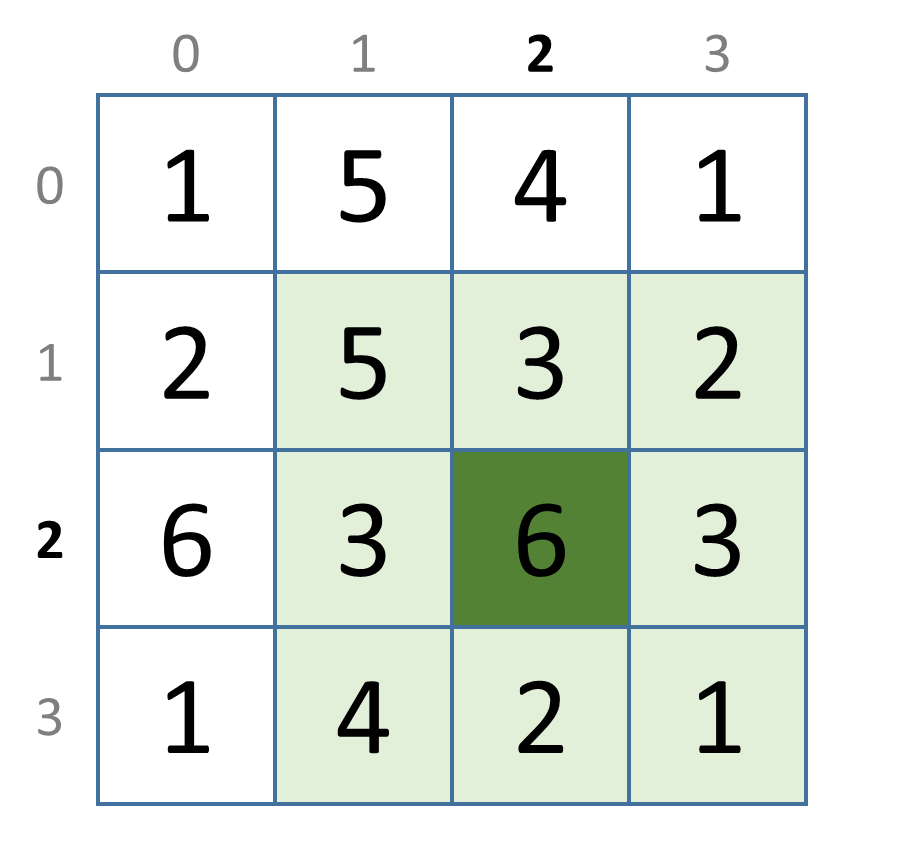
>>> neighbours(2, 2, grid)
{1, 2, 3, 4, 5}
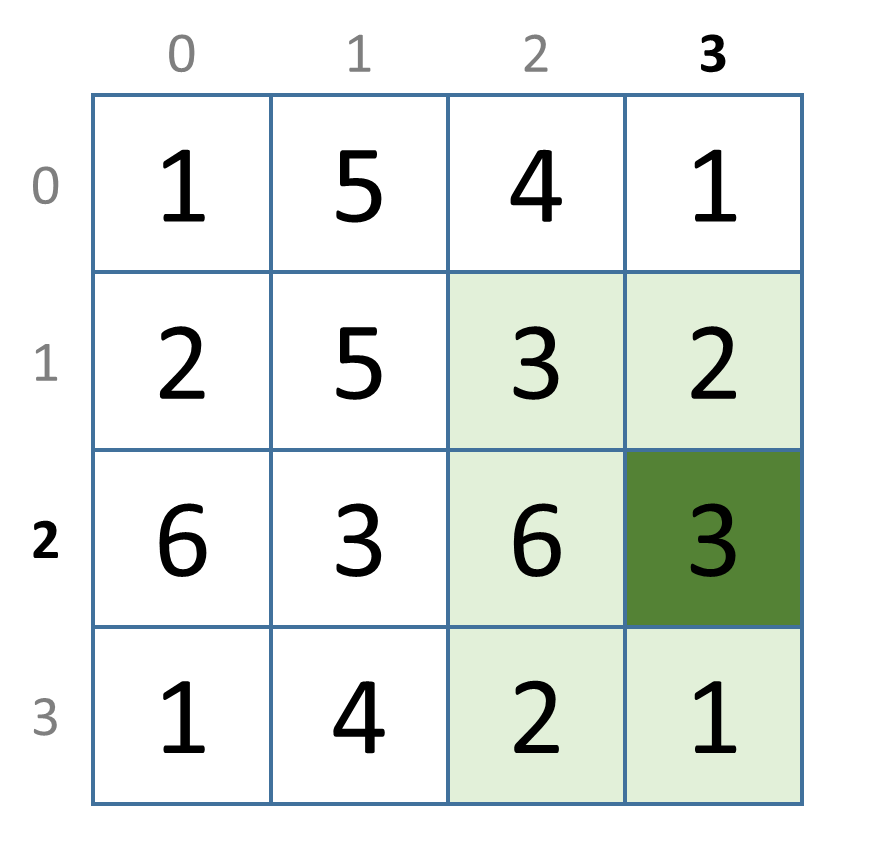
>>> neighbours(2, 3, grid)
{1, 2, 3, 6}
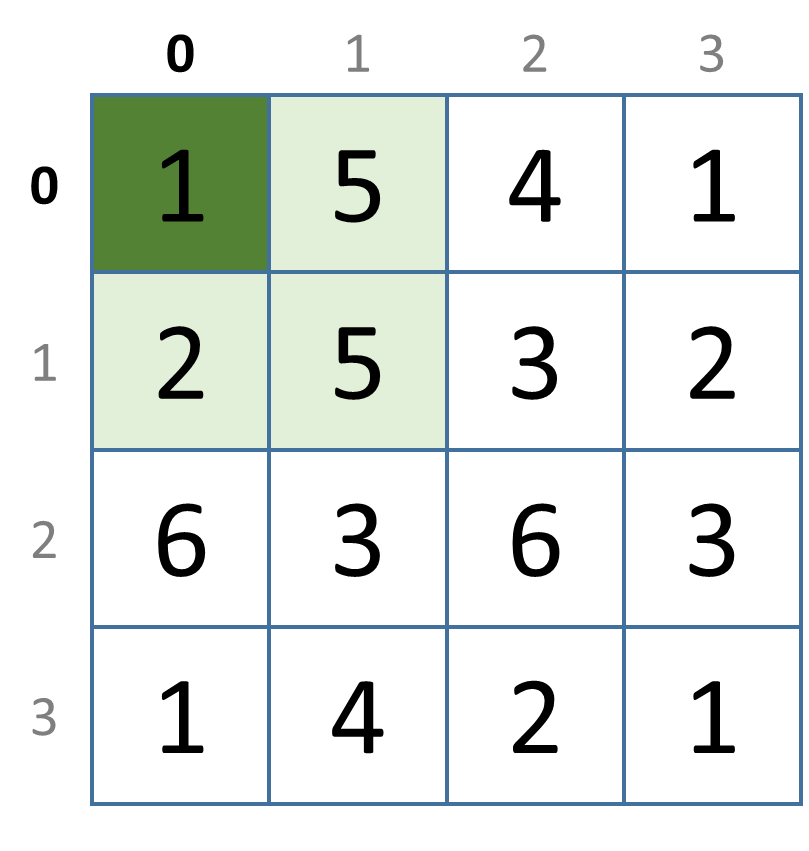
>>> neighbours(0, 0, grid)
{2, 5}
>>> neighbours(4, 4, grid)
Traceback (most recent call last):
AssertionError: invalid position

>>> isAdjacent('111222333', 3)
False
>>> isAdjacent('123321123', 3)
True
>>> isAdjacent('424313424', 3)
True
>>> isAdjacent('1541253263631421', 4)
True
>>> isAdjacent('1541253263631421', 5)
Traceback (most recent call last):
AssertionError: invalid string representation

Below we give a graphical representation of all adjacent cells (light green) for each of the cells (dark green) that are used to test the function neighbours in the above interactive session.