Hieronder de formules voor de \(n\)-de macht van een tweeterm \((a+b)^n\):

\[(a+b)^0 = 1\] \[(a+b)^1 = a + b\] \[(a+b)^2 = a^2 + 2ab + b^2\] \[(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3\] \[(a+b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4\]

De coëfficiënten die gebruikt worden kan je gemakkelijk terugvinden in de driehoek van Pascal:

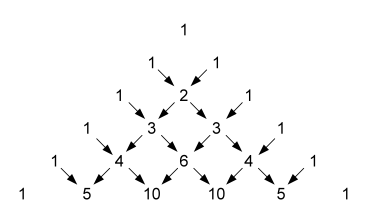
Driehoek pascal

Elk getal uit deze driehoek is de som van twee bovenliggende getallen (zie figuur). Merk op dat er ook een rechtstreekse formule bestaat voor deze getallen, die ook binomiaalcoëfficiënten genoemd worden omdat ze de coëfficiënten zijn bij de ontwikkeling van tweetermen (binomialen). Je kan deze formules makkelijk opzoeken, maar het is NIET de bedoeling dat je die formules voor deze oefening gebruikt. Elke rij getallen moet uit de vorige rij afgeleid worden!!

Opgave

Schrijf een functie coefficienten(n) die de coëfficiënten van de \(n\)-de macht teruggeeft als list.
Schrijf een functie formule(n) die de juiste formuler berekent voor \((1 + x)^n\), en deze als string teruggeeft. Roep de vorige functie aan om de coëfficiënten te bepalen.

Voorbeeld

>>> coefficienten(3)
[1, 3, 3, 1]

>>> formule(3)
"1 + 3x + 3x^2 + x^3"