These three 10-digit sequences have an elegant property.
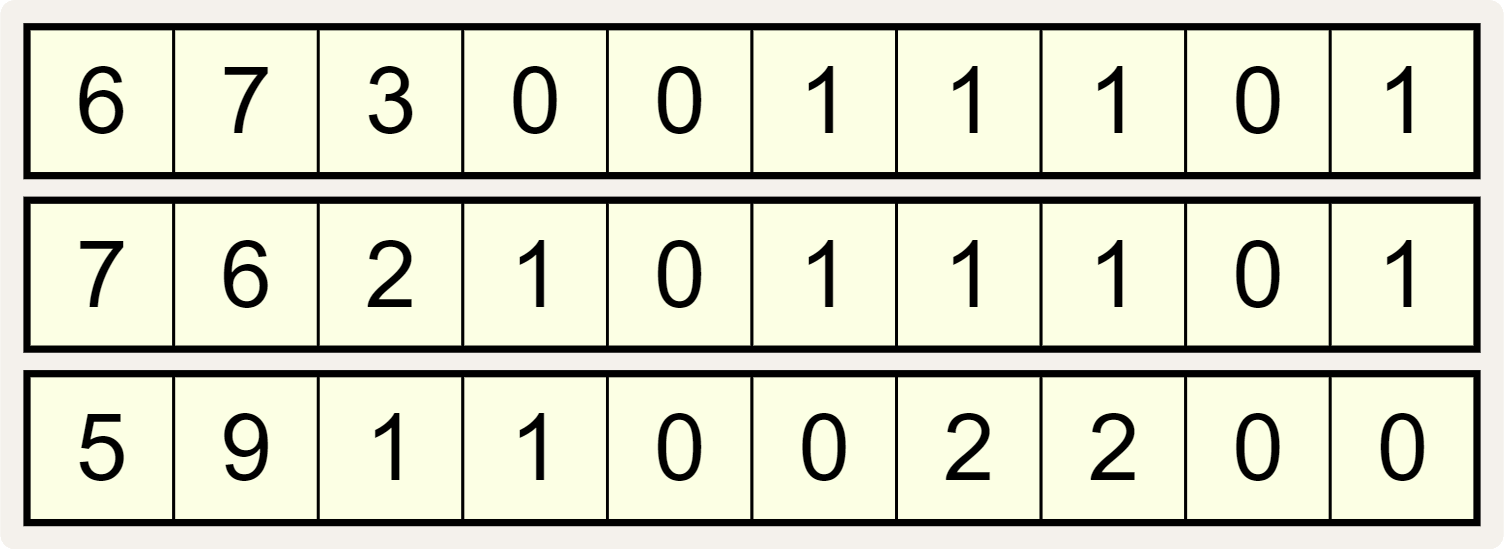
If we number the positions of the digits in each sequence from left to right, starting from 0 — seen as the gray column numbers in the header below — then each digit in column $$i$$ ($$i = 0, 1, \ldots, 9)$$ of a sequence records how many times column index $$i$$ occurs as a digit in the other two sequences.
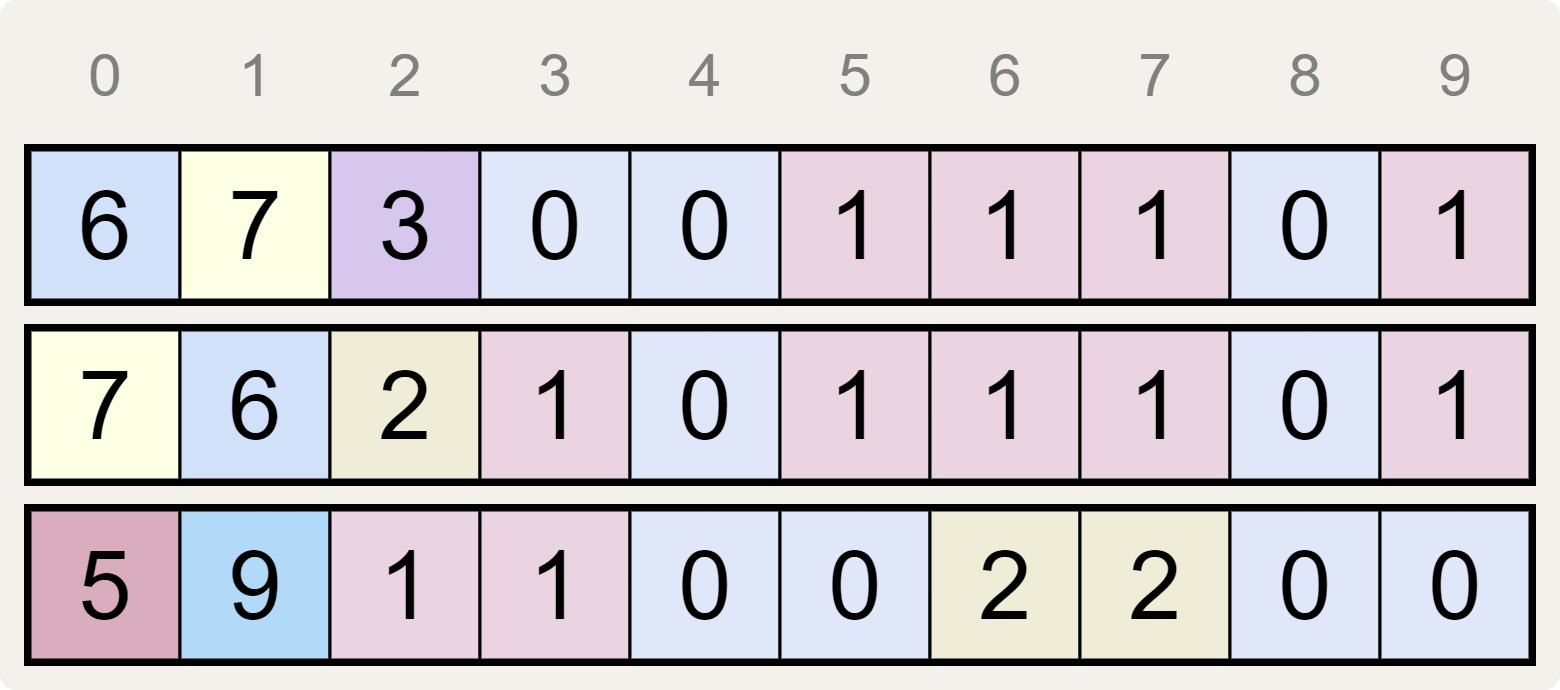
Hence the leftmost 6 in the top sequence identifies the number of zeros (0) in the bottom two sequences, as you can verify. And likewise for every digit in all three sequences.
Assignment
The elegant property does not simply apply to any three 10-digit sequences. For example, if we consider these three sequences
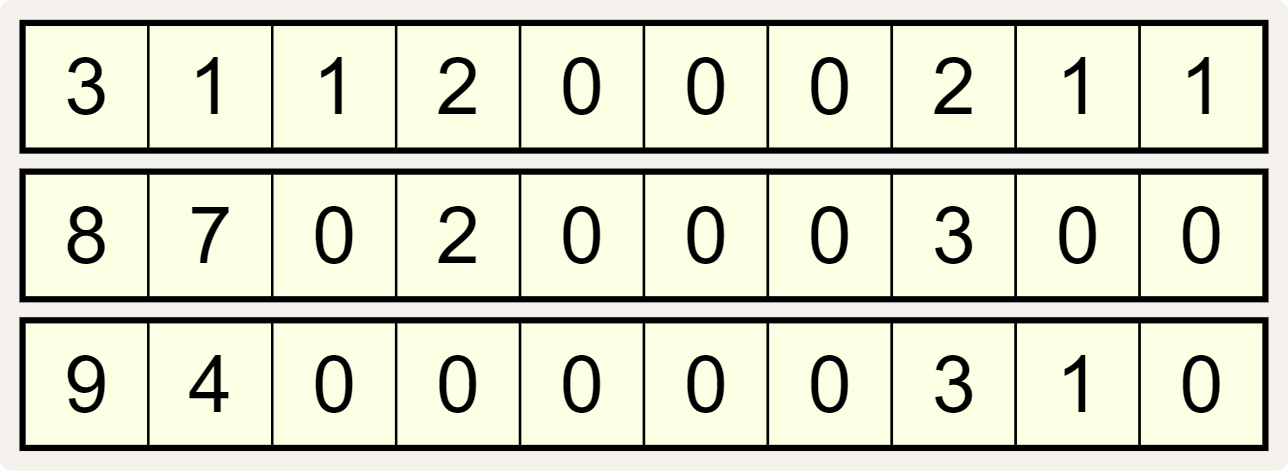
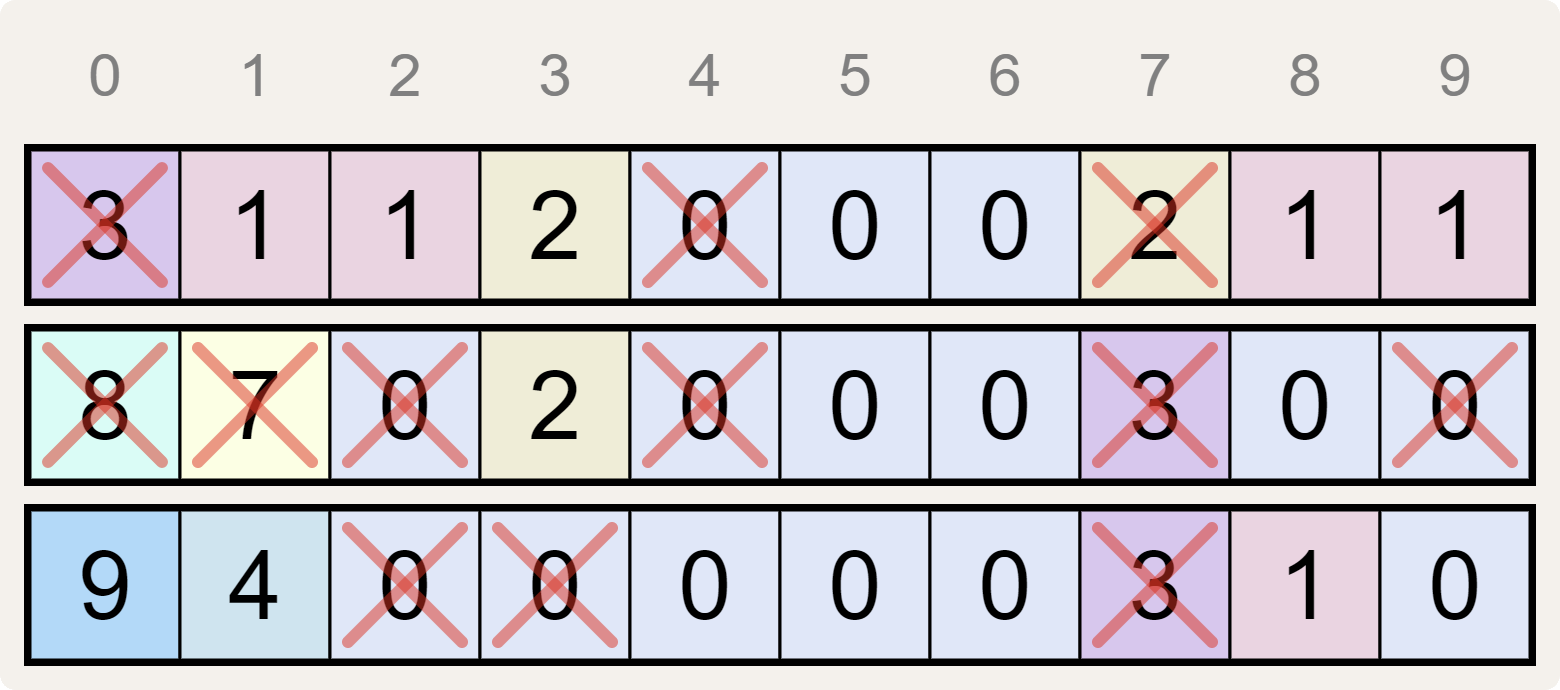
then their representation below has a red cross drawn through each digit that does not match the number of occurrences of its column index $$i$$ ($$i = 0, 1, \ldots, 9$$) in the other two 10-digit sequences.
Input
Three 10-digit sequences, each on a separate line.
Output
The three 10-digit sequences from the input, each on a separate line, with each digit not matching the number of occurrences of its column index $$i$$ ($$i = 0, 1, \ldots, 9$$) in the other two sequences replaced by the uppercase letter X.
DRY
Don't repeat yourself: avoid any unnecessary repetition in your code.
Don't repeat yourself: avoid any unnecessary repetition in your code.
Example
Input:
6730011101
7621011101
5911002200Output:
6730011101
7621011101
5911002200Example
Input:
3112000211
8702000300
9400000310Output:
X112X00X11
XXX2X00X0X
94XX000X10