In the previous assignment, we have represented a polymer as a list containing the positions of the successive monomers of the polymer. Each position is represented as a tuple $$(x,y)$$, where $$x,y \in \mathbb{Z}$$. The first monomer is always placed at the origin $$(0,0)$$ of the Cartesian plane, and the next position is always one unit step up, down, left or right of the previous position. Two monomers of the same polymer can never occupy the same position.

Assignment

Write a function showPolymerwhich prints the structure of a polymer for a given list of positions of the monomers of a polymer (which is to be passed to the function as argument). To do this, just follow these steps:

Define a two-dimensional matrix $$P$$ (such as a list of lists) to build the structure of the polymer in. Initially all the elements of this matrix contain a string consisting of a single space.
The even rows and columns of the matrix are used to indicate where the monomers of the polymer are located. Monomers are indicated by the letter o, with the exception of the first monomer that is designated by the letter x and the last monomer which is indicated with an asterisk (*). For each monomer at position $$(x,y)$$ the space in the matrix at position $$P_{i,j}$$ is replaced by the character that represents the monomer, wherein
\[\begin{cases} \, i = 2\,(y_{\max} - y) \\ \, j = 2\,(x - x_{\min}) \end{cases} \]if we assume that the rows and columns of the matrix are indexed from 0. Here $$x_{\min}$$ is the minimum $$x$$-co-ordinate of all monomers in the polymer, and $$y_{\max}$$ is the maximum $$y$$-co-ordinate of all the monomers in the polymer.
On the odd-numbered rows and columns of the matrix, we connect the successive monomers of the polymer with each other. Two consecutive monomers that are left and right of each other, are connected by a hyphen (-) bridge between the two positions of the monomers in the matrix. Two consecutive monomers above and below each other are connected by a vertical bar (|). After the preceding steps, the matrix that corresponds to the list representation of the polymer
```
(0, 0), (1, 0), (2, 0), (3, 0), (4, 0), (4, 1), (4, 2), 
(4, 3), (3, 3), (2, 3), (2, 2), (2, 1), (3, 1), (3, 2)
```
looks like

matrix representation of a random walk

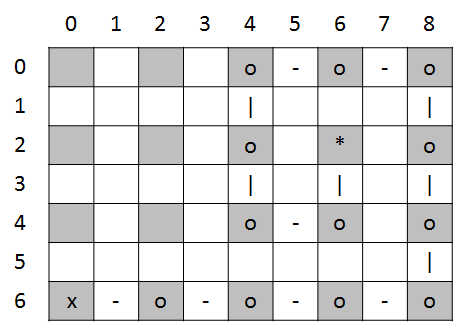
The empty cells in the matrix representation still contain a string that consists of a single space.
The output is generated by printing the rows of the matrix one by one (from top to bottom), in which the various characters in the columns of the same row are written one after the other. The preceding example then delivers the following output.
```
    o-o-o
    |   |
    o * o
    | | |
    o-o o
        |
x-o-o-o-o
```

Example

>>> polymer1 = [(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (1, 2), (0, 2), 
...              (0, 1), (1, 1)]
>>> showPolymer(polymer1)
o-o-o
|   |
o-* o
    |
x-o-o
>>> polymer2 = [(0, 0), (1, 0), (2, 0), (2, -1), (3, -1), (4, -1), (4, 0), 
...              (4, 1), (3, 1), (3, 0)]
>>> showPolymer(polymer2)
      o-o
      | |
x-o-o * o
    |   |
    o-o-o
>>> polymer3 = [(0, 0), (0, -1), (1, -1), (1, -2), (1, -3), (1, -4), (0, -4), 
...              (0, -3), (-1, -3), (-2, -3), (-2, -2), (-2, -1), (-1, -1), 
...              (-1, -2), (0, -2)]
>>> showPolymer(polymer3)
    x  
    |  
o-o o-o
| |   |
o o-* o
|     |
o-o-o o
    | |
    o-o