A long time ago there lived a rich farmer who had sixteen children, eight by his first wife who was deceased and eight by his second wife. His second wife, however, wanted to ensure that her eldest son would inherit the property of the farmer. That's why one day she made him the following proposal:
Dearest husband, you're getting older. We urgently need to determine who will be your heir. Let us line up the sixteen children in a circle. Starting with one of the children, we can then clockwise remove every tenth child out of the circle until only one child remains to whom you'll leave your property.
The farmer accepted the proposal. However, after the seventh child was removed from the circle the farmer noticed that all children who had previously been removed from the circle were children of his first wife. The farmer stopped the selection, because he could see that the last child he had with his first wife was next in line to be removed from the circle.
The farmer suggested to resume where they had come after the seventh child was removed from the circle, but to begin counting counterclockwise from that point. The woman — forced to decide quickly — agreed because she believed the odds were in her favour. Who eventually became the heir to the farmer?
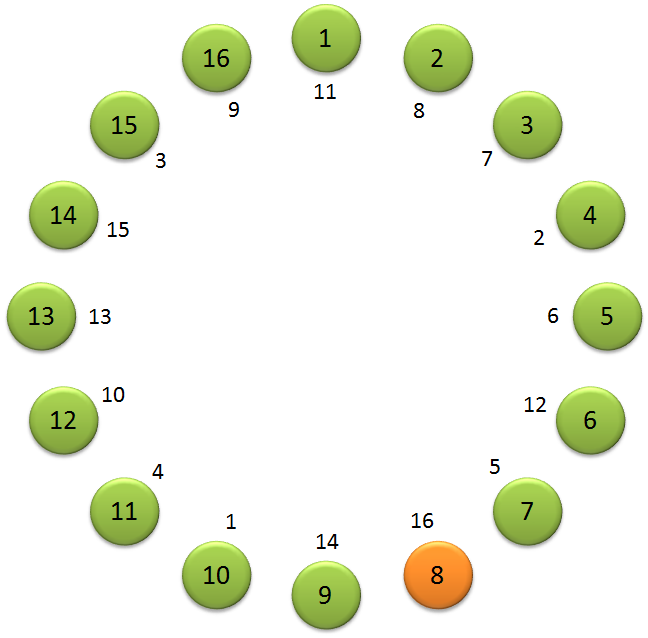
If the selection is applied to a farmer who has eight children with each wife, and each tenth child is removed from the circle, then the child at position eight is heir to the farmer. The circles represent the children. The numbers in the circles represents a numbering of the children, which we have numbered beginning with 1 for the child on top of the circle and continuing clockwise. The numbers on the inside of the circle indicate the order in which the children are removed from the circle in the selection process.
Assignment
A farmer has $$k$$ children with each of his two wives. All the children
are placed in a circle, and numbered clockwise from 1 to $$2k$$. We start
counting clockwise from child number 1, where each $$n$$-th child is
removed from circle. After $$k - 1$$ children were removed from the
circle, the continues counterclockwise. The circle gets smaller and
smaller, and the last child that remains is the heir to the farmer.
Write a function heir to which the values $$k$$ and $$n$$
must be passed, in which you may assume that $$k \geq 2$$. The function
should return a list indicating the order in which the children were
removed from the circle. The first child removed is thus first in the
list, and the eventual heir last in the list. Use the serial numbers of
the children as elements in the list.
Example
>>> heir(8, 10)
[10, 4, 15, 11, 7, 5, 3, 2, 16, 12, 1, 6, 13, 9, 14, 8]
>>> heir(8, 3)
[3, 6, 9, 12, 15, 2, 7, 1, 13, 8, 16, 10, 14, 4, 11, 5]
>>> heir(10, 5)
[5, 10, 15, 20, 6, 12, 18, 4, 13, 3, 16, 7, 14, 1, 8, 9, 2, 17, 11, 19]