The United States counts its citizens every ten years, and the result of that census is used to allocate the 435 congressional seats in the House of Representatives1 to the 50 states. Since 1940, that allocation has been done using a method devised by Edward Vermilye Huntington2 and Joseph Adna Hill3.

The Huntington-Hill method4 begins by assigning one representative to each state. Then each of the remaining representatives is assigned to a state in a succession of rounds by computing \[g(n, p) = \frac{p}{\sqrt{n(n+1)}}\] for each state, where $$n$$ is the current number of representatives (initially 1) and $$p$$ is the population of the state. This way, the value $$g(n, p)$$ represents the state's population divided by the geometric mean5 of the current number of representatives and the number of representatives that the state would have if it was assigned the next representative. The geometric mean $$g(n, p)$$ is calculated for each state at each round and the next representative is assigned to the state with the highest geometric mean $$g(n, p)$$.
For instance, once a state has been assigned one representative, the geometric mean $$g(n, p)$$ for each state is its population divided the square root of 2. Since California has the biggest population, it gets the 51st representative. Then its geometric mean $$g(n, p)$$ is recalculated as its population divided by the square root of $$2 \times 3 = 6$$, and in the second round the 52nd representative is assigned to Texas, which has the second-highest population, since it now has the largest geometric mean $$g(n, p)$$. This continues for $$435 - 50 = 385$$ rounds until all the representatives have been assigned.
Assignment
We will work with comma-separated values files6 (CSV-files) that contain the results of one or more censuses. The first column contains the names of the regions (e.g. the states of the United States) whose population counts are reported. Each remaining column contains the population count per region for the census in the year indicated in the column header. As an example, here are the first few lines of such a CSV-file:
REGION,1910,1920,1930,1940,1950,1960,1970,1980,1990,2000,2010 Alabama,2138093,2348174,2646248,2832961,3061743,3266740,3444165,3893888,4040587,4447100,4779736 Alaska,64356,55036,59278,72524,128643,226167,300382,401851,550043,626932,710231 Arizona,204354,334162,435573,499261,749587,1302161,1770900,2718215,3665228,5130632,6392017 Arkansas,1574449,1752204,1854482,1949387,1909511,1786272,1923295,2286435,2350725,2673400,2915918 California,2377549,3426861,5677251,6907387,10586223,15717204,19953134,23667902,29760021,33871648,37253956 Colorado,799024,939629,1035791,1123296,1325089,1753947,2207259,2889964,3294394,4301261,5029196 Connecticut,1114756,1380631,1606903,1709242,2007280,2535234,3031709,3107576,3287116,3405565,3574097 Delaware,202322,223003,238380,266505,318085,446292,548104,594338,666168,783600,897934 Florida,752619,968470,1468211,1897414,2771305,4951560,6789443,9746324,12937926,15982378,18801310
...
Your task is to define a class Census that can be used to allocate a certain number of representatives over a number of regions according to the Huntington-Hill method, based on the population counts of the regions as stored in a CSV-file. This class must at least support the following methods:
-
A method __init__ that takes a year (int) and the location (str) of a CSV-file. The CSV-file must contain the results of one or more censuses, but the object should only use the population counts found in the column whose header corresponds to the given year. In case the CSV-file has no column whose header corresponds to the given year, an AssertionError must be raised with the message no data available.
-
A method citizens that takes the name (str) of a region. If no population count is available for the given name of the region, an AssertionError must be raised with the message no data available. Otherwise, the method must return the population count (int) of that region, based on the census data in the year that was passed to the initialization method.
-
A method allocation that takes a number of representatives (int) that needs to be allocated. If the number of representatives is smaller than the number of regions in the CSV-file that was passed to the initialization method, an AssertionError must be raised with the message too few representatives. Otherwise, the method must return a dictionary (dict) whose keys are the names (str) of all regions in the CSV-file that was passed to the initialization method. The dictionary must map each region onto the number of representatives (int) allocated to that region according to the Huntington-Hill method.
Example
In the following interactive session, we assume the CSV-file us_population.csv7 to be located in the current directory.
>>> us2010 = Census(2010, 'us_population.csv8')
>>> us2010.citizens('Alabama')
4779736
>>> us2010.citizens('Hawaii')
1360301
>>> us2010.citizens('Wyoming')
563626
>>> us2010.citizens('Calisota')
Traceback (most recent call last):
AssertionError: no data available
>>> us2010.allocation(435)
{'Oklahoma': 5, 'Illinois': 18, 'Pennsylvania': 18, 'Iowa': 4, 'Maine': 2, 'South Dakota': 1, 'Nebraska': 3, 'New Jersey': 12, 'Maryland': 8, 'Texas': 36, 'Alabama': 7, 'Idaho': 2, 'South Carolina': 7, 'Michigan': 14, 'Tennessee': 9, 'Kansas': 4, 'Wyoming': 1, 'Wisconsin': 8, 'Louisiana': 6, 'Nevada': 4, 'Vermont': 1, 'Massachusetts': 9, 'Kentucky': 6, 'California': 53, 'Missouri': 8, 'Colorado': 7, 'Arizona': 9, 'Florida': 27, 'Utah': 4, 'Virginia': 11, 'Alaska': 1, 'New Mexico': 3, 'Ohio': 16, 'Oregon': 5, 'Hawaii': 2, 'Indiana': 9, 'North Carolina': 13, 'New York': 27, 'Delaware': 1, 'Minnesota': 8, 'West Virginia': 3, 'New Hampshire': 2, 'Arkansas': 4, 'Montana': 1, 'Georgia': 14, 'Connecticut': 5, 'Rhode Island': 2, 'Mississippi': 4, 'Washington': 10, 'North Dakota': 1}
>>> us2010.allocation(1024)
{'Oklahoma': 12, 'Illinois': 43, 'Pennsylvania': 42, 'Iowa': 10, 'Maine': 4, 'South Dakota': 3, 'Nebraska': 6, 'New Jersey': 29, 'Maryland': 19, 'Texas': 84, 'Alabama': 16, 'Idaho': 5, 'South Carolina': 15, 'Michigan': 33, 'Tennessee': 21, 'Kansas': 9, 'Wyoming': 2, 'Wisconsin': 19, 'Louisiana': 15, 'Nevada': 9, 'Vermont': 2, 'Massachusetts': 22, 'Kentucky': 14, 'California': 124, 'Missouri': 20, 'Colorado': 17, 'Arizona': 21, 'Florida': 63, 'Utah': 9, 'Virginia': 27, 'Alaska': 2, 'New Mexico': 7, 'Ohio': 38, 'Oregon': 13, 'Hawaii': 5, 'Indiana': 22, 'North Carolina': 32, 'New York': 64, 'Delaware': 3, 'Minnesota': 18, 'West Virginia': 6, 'New Hampshire': 4, 'Arkansas': 10, 'Montana': 3, 'Georgia': 32, 'Connecticut': 12, 'Rhode Island': 4, 'Mississippi': 10, 'Washington': 22, 'North Dakota': 2}
>>> us2010.allocation(42)
Traceback (most recent call last):
AssertionError: too few representatives
>>> Census(1900, 'us_population.csv9')
Traceback (most recent call last):
AssertionError: no data available
Epilogue
Calisota10 is a fictional U.S. state, created by Carl Banks11 in his story The Gilded Man12 (1952) from the Donald Duck comic-book series. Duckburg13 — the home town of Donald Duck and his family — is one of the most important cities located in Calisota, as well as Goosetown — which Duckburg maintains a traditional rivalry with — and Mouseton14.
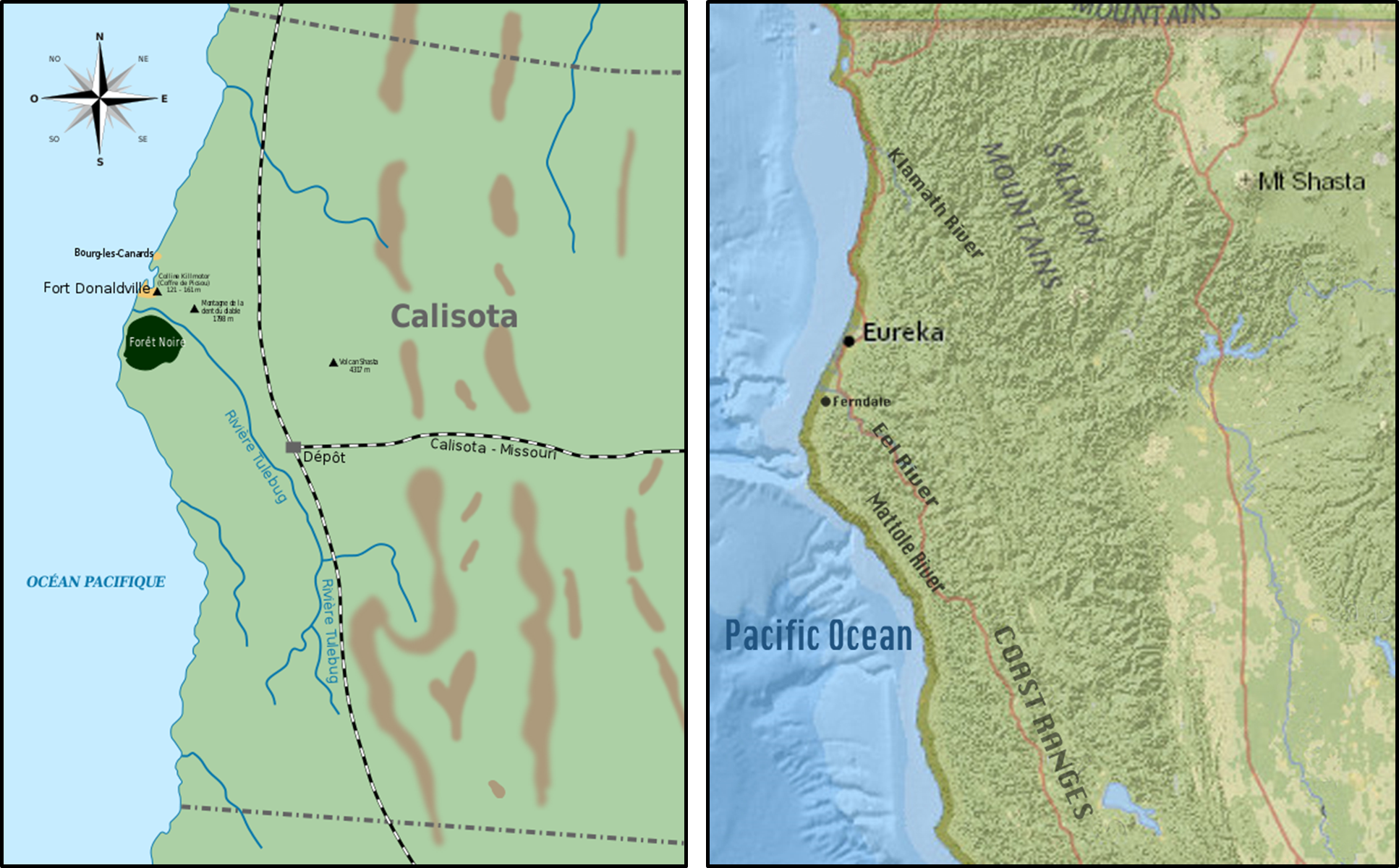
Although it has many fictional elements and a variable climate, Calisota is probably roughly equivalent to Northern California. Duckburg is located north of San Francisco, with a map in Don Rosa15's The Life and Times of Scrooge McDuck16 showing Calisota corresponding to the part of California north of Sacramento.
The name is a blend of California and Minnesota, supposedly to allow all kinds of weather or climate in the stories, although Calisota bears very little in common with the latter (a state in the Upper Midwest, far from the ocean coasts) and Northern California region weather is sufficiently variable by itself.