The United States counts its citizens every ten years, and the result of that census is used to allocate the 435 congressional seats in the House of Representatives to the 50 states. Since 1940, that allocation has been done using a method devised by Edward Vermilye Huntington and Joseph Adna Hill.

The Huntington-Hill method begins by assigning one representative to each state. Then each of the remaining representatives is assigned to a state in a succession of rounds by computing \[g(n, p) = \frac{p}{\sqrt{n(n+1)}}\] for each state, where $$n$$ is the current number of representatives (initially 1) and $$p$$ is the population of the state. This way, the value $$g(n, p)$$ represents the state's population divided by the geometric mean of the current number of representatives and the number of representatives the state would have if it was assigned the next representative. The geometric mean $$g(n, p)$$ is calculated for each state at each round and the next representative is assigned to the state with the highest geometric mean $$g(n, p)$$.

For instance, once each state has been assigned one representative, the geometric mean $$g(n, p)$$ for each state is its population divided the square root of 2. Since California has the biggest population, it gets the 51^st representative. Then its geometric mean $$g(n, p)$$ is recalculated as its population divided by the square root of $$2 \times 3 = 6$$. In the second round the 52^nd representative is assigned to Texas, which has the second-highest population, since it now has the largest geometric mean $$g(n, p)$$. This continues for $$435 - 50 = 385$$ rounds until all the representatives have been assigned.

Assignment

We will work with comma-separated values files (CSV-files) that contain the results of one or more censuses. The first column contains the names of the regions (e.g. the states of the United States) whose population counts are reported. Each remaining column contains the population count per region for the census in the year indicated in the column header. As an example, here are the first few lines of such a CSV-file:

REGION,1910,1920,1930,1940,1950,1960,1970,1980,1990,2000,2010,2020
Alabama,2138093,2348174,2646248,2832961,3061743,3266740,3444165,3893888,4040587,4447100,4779736,5024279
Alaska,64356,55036,59278,72524,128643,226167,300382,401851,550043,626932,710231,733391
Arizona,204354,334162,435573,499261,749587,1302161,1770900,2718215,3665228,5130632,6392017,7151502
Arkansas,1574449,1752204,1854482,1949387,1909511,1786272,1923295,2286435,2350725,2673400,2915918,3011524
California,2377549,3426861,5677251,6907387,10586223,15717204,19953134,23667902,29760021,33871648,37253956,39538223
Colorado,799024,939629,1035791,1123296,1325089,1753947,2207259,2889964,3294394,4301261,5029196,5773714
Connecticut,1114756,1380631,1606903,1709242,2007280,2535234,3031709,3107576,3287116,3405565,3574097,3605944
Delaware,202322,223003,238380,266505,318085,446292,548104,594338,666168,783600,897934,989948
Florida,752619,968470,1468211,1897414,2771305,4951560,6789443,9746324,12937926,15982378,18801310,21538187
…

Define a class Census that can be used to allocate a certain number of representatives over a number of regions according to the Huntington-Hill method, based on the population counts of the regions as stored in a CSV-file.

When creating a new census $$c$$ (Census), a year (int) and the location (str) of a CSV-file must be passed. The CSV-file must contain the results of one or more censuses, but census $$c$$ should only use the population counts found in the column whose header corresponds to the given year. In case the CSV-file has no column whose header corresponds to the given year, an AssertionError must be raised with the message no data available.

In addition, it should be possible to call at least the following methods on a census $$c$$ (Census):

• A method citizens that takes the name of a region $$r$$ (str). If no population count is available for region $$r$$, an AssertionError must be raised with the message no data available. Otherwise, the method must return the population count (int) of region $$r$$, based on the census data in the year passed when creating census $$c$$.

• A method allocation that takes a number of representatives (int) that needs to be allocated. If the number of representatives is smaller than the number of regions in the CSV-file passed when creating census $$c$$, an AssertionError must be raised with the message too few representatives. Otherwise, the method must return a dictionary (dict) whose keys are the names (str) of all regions in the CSV-file passed when creating census $$c$$. The dictionary must map each region onto the number of representatives (int) allocated to that region according to the Huntington-Hill method, based on the population counts in the year passed when creating census $$c$$.

Example

In the following interactive session, we assume the CSV-file us_population.csv to be located in the current directory.

>>> us2010 = Census(2010, 'us_population.csv')
>>> us2010.citizens('Alabama')
4779736
>>> us2010.citizens('Hawaii')
1360301
>>> us2010.citizens('Wyoming')
563626
>>> us2010.citizens('Calisota')
Traceback (most recent call last):
AssertionError: no data available
>>> us2010.allocation(435)
{'Oklahoma': 5, 'Illinois': 18, 'Pennsylvania': 18, 'Iowa': 4, 'Maine': 2, 'South Dakota': 1, 'Nebraska': 3, 'New Jersey': 12, 'Maryland': 8, 'Texas': 36, 'Alabama': 7, 'Idaho': 2, 'South Carolina': 7, 'Michigan': 14, 'Tennessee': 9, 'Kansas': 4, 'Wyoming': 1, 'Wisconsin': 8, 'Louisiana': 6, 'Nevada': 4, 'Vermont': 1, 'Massachusetts': 9, 'Kentucky': 6, 'California': 53, 'Missouri': 8, 'Colorado': 7, 'Arizona': 9, 'Florida': 27, 'Utah': 4, 'Virginia': 11, 'Alaska': 1, 'New Mexico': 3, 'Ohio': 16, 'Oregon': 5, 'Hawaii': 2, 'Indiana': 9, 'North Carolina': 13, 'New York': 27, 'Delaware': 1, 'Minnesota': 8, 'West Virginia': 3, 'New Hampshire': 2, 'Arkansas': 4, 'Montana': 1, 'Georgia': 14, 'Connecticut': 5, 'Rhode Island': 2, 'Mississippi': 4, 'Washington': 10, 'North Dakota': 1}
>>> us2010.allocation(1024)
{'Oklahoma': 12, 'Illinois': 43, 'Pennsylvania': 42, 'Iowa': 10, 'Maine': 4, 'South Dakota': 3, 'Nebraska': 6, 'New Jersey': 29, 'Maryland': 19, 'Texas': 84, 'Alabama': 16, 'Idaho': 5, 'South Carolina': 15, 'Michigan': 33, 'Tennessee': 21, 'Kansas': 9, 'Wyoming': 2, 'Wisconsin': 19, 'Louisiana': 15, 'Nevada': 9, 'Vermont': 2, 'Massachusetts': 22, 'Kentucky': 14, 'California': 124, 'Missouri': 20, 'Colorado': 17, 'Arizona': 21, 'Florida': 63, 'Utah': 9, 'Virginia': 27, 'Alaska': 2, 'New Mexico': 7, 'Ohio': 38, 'Oregon': 13, 'Hawaii': 5, 'Indiana': 22, 'North Carolina': 32, 'New York': 64, 'Delaware': 3, 'Minnesota': 18, 'West Virginia': 6, 'New Hampshire': 4, 'Arkansas': 10, 'Montana': 3, 'Georgia': 32, 'Connecticut': 12, 'Rhode Island': 4, 'Mississippi': 10, 'Washington': 22, 'North Dakota': 2}
>>> us2010.allocation(42)
Traceback (most recent call last):
AssertionError: too few representatives

>>> Census(1900, 'us_population.csv')
Traceback (most recent call last):
AssertionError: no data available

Epilogue

Calisota is a fictional U.S. state, created by Carl Banks in his story The Gilded Man (1952) from the Donald Duck comic-book series. Duckburg — the home town of Donald Duck and his family — is one of the most important cities located in Calisota, as well as Goosetown — which Duckburg maintains a traditional rivalry with — and Mouseton.

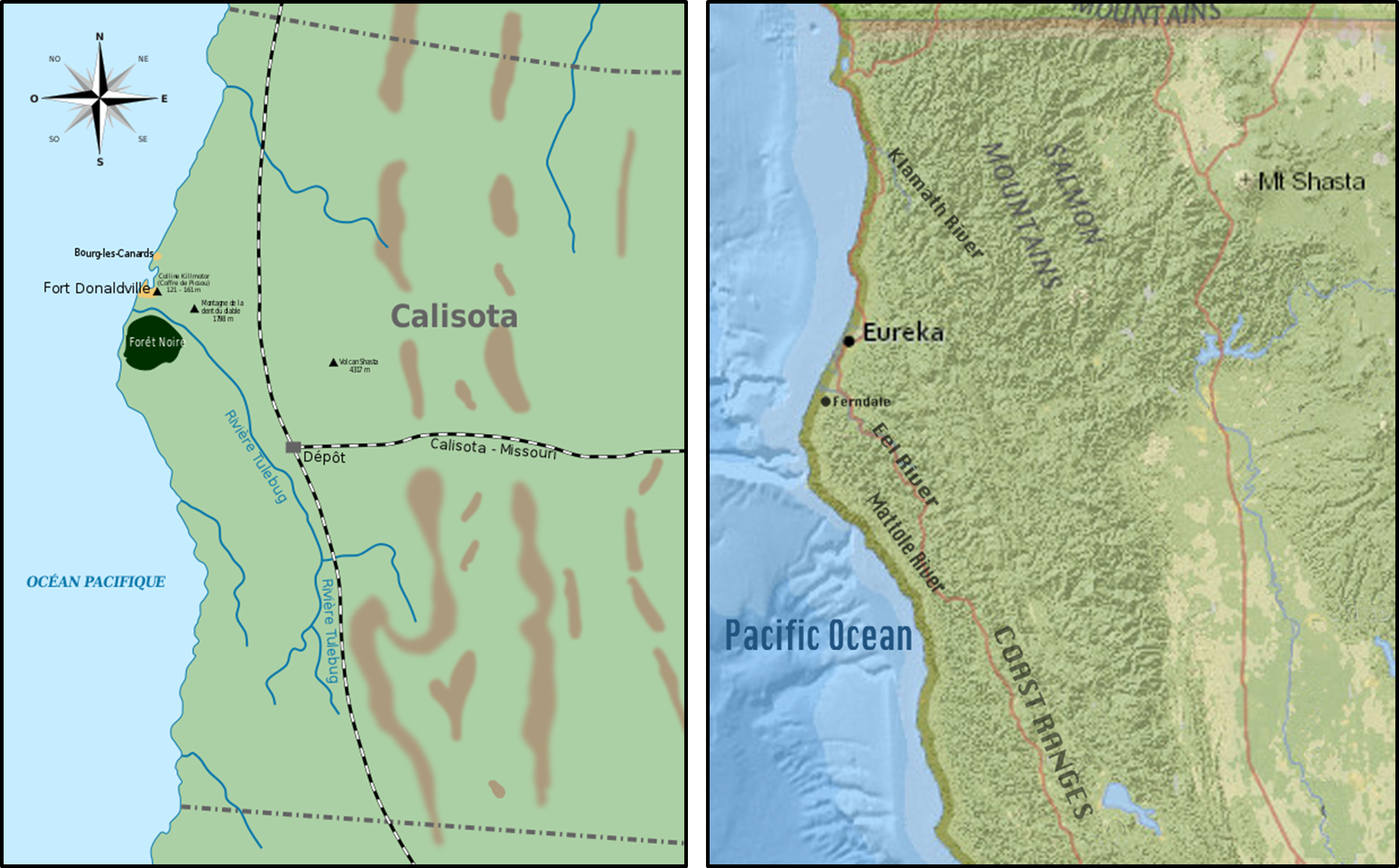
Although it has many fictional elements and a variable climate, Calisota is probably roughly equivalent to Northern California. Duckburg is located north of San Francisco, with a map in Don Rosa's The Life and Times of Scrooge McDuck showing Calisota corresponding to the part of California north of Sacramento.

The name is a blend of California and Minnesota, supposedly to allow all kinds of weather or climate in the stories, although Calisota bears very little in common with the latter (a state in the Upper Midwest, far from the ocean coasts) and Northern California region weather is sufficiently variable by itself.