In Ancient China, soldiers stationed along the Great Wall would alert each other of impending enemy attack by signaling from tower to tower. This enabled them to transmit a message as far away as 750 kilometers in just a few hours.

The fortifications along the Great Wall of China are not positioned in a straight line, but form a network of walls made of stone, brick, tampered earth and wood that connect a series of watchtowers with each other. Watchtowers used to spread smoke signals are usually built on top of a hummock to optimize the observation of the signals.

Assignment

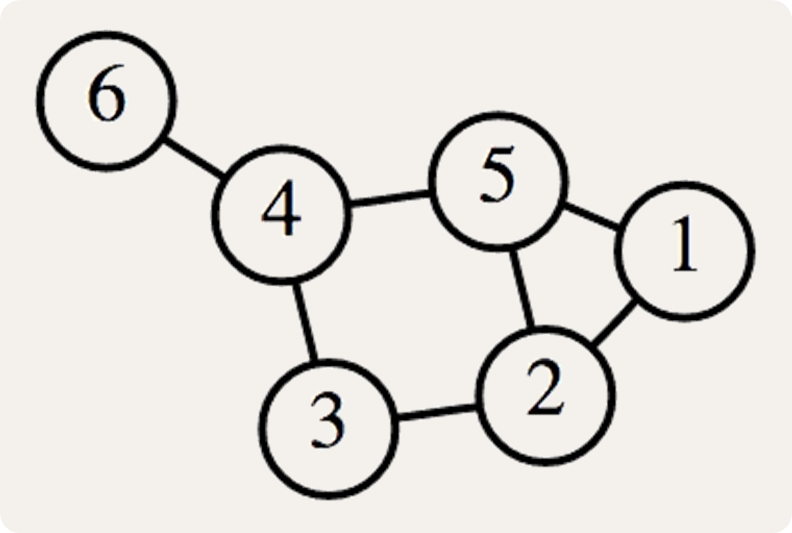
An example network of guard posts along the Great Wall of China where smoke signals can be released is depicted below. The guard posts are represented as circles, with each watchtower labeled by an integer. Two watchtowers are connected by a line if smoke signals released from one of the towers can be observed at the other watchtower. As such, a smoke signal released at watchtower 6 in this network can only be observed at watchtower 4. A smoke signal released at watchtower 1 can be observed at watchtowers 2 and 5. As soon as a guard post observes a smoke signal, it starts releasing smoke signals at its own watchtower in order to spread the alarm along the entire network.

Each watchtower is represented by an integer (int) that uniquely identifies the guard post.

A network of guard posts is represented as a dictionary (dict) that maps each watchtower (int) in the network onto a set of all neighboring watchtowers (int) in the network where its smoke signals can be observed. All guard posts in the network are always connected to each other via neighboring guard posts. The example network depicted above is thus represented by the following dictionary:

{1:{2, 5}, 2:{1, 5, 3}, 3:{2, 4}, 4:{3, 5, 6}, 5:{1, 2, 4}, 6:{4}}

Your task:

• Write a function observed that takes two arguments: i) a set of all watchtowers (int) in a network where smoke signals are released and ii) the network of guard posts (dict). The function must return a set of all watchtowers (int) in the network where smoke signals are observed but that do not release a smoke signal themselves.

• Write a function distribution that takes two arguments: i) a watchtower $$t$$ (int) and ii) the network of guard posts (dict). At time zero, a smoke signal is released at watchtower $$t$$ to start spreading an alarm. After each time step, additional smoke signals are released at all watchtowers where smoke signals are observed. The function must return an integer (int) that indicates after how many time steps the alarm has been spread across all watchtowers in the network.

Example

>>> network = {1:{2, 5}, 2:{1, 5, 3}, 3:{2, 4}, 4:{3, 5, 6}, 5:{1, 2, 4}, 6:{4}}

>>> observed({1, 2}, network)
{3, 5}
>>> observed({3, 4}, network)
{2, 5, 6}

>>> distribution(1, network)
3
>>> distribution(4, network)
2