Bij het spelletje Codenames nemen twee rivaliserende geheime diensten het tegen elkaar op: team rood tegen team blauw.

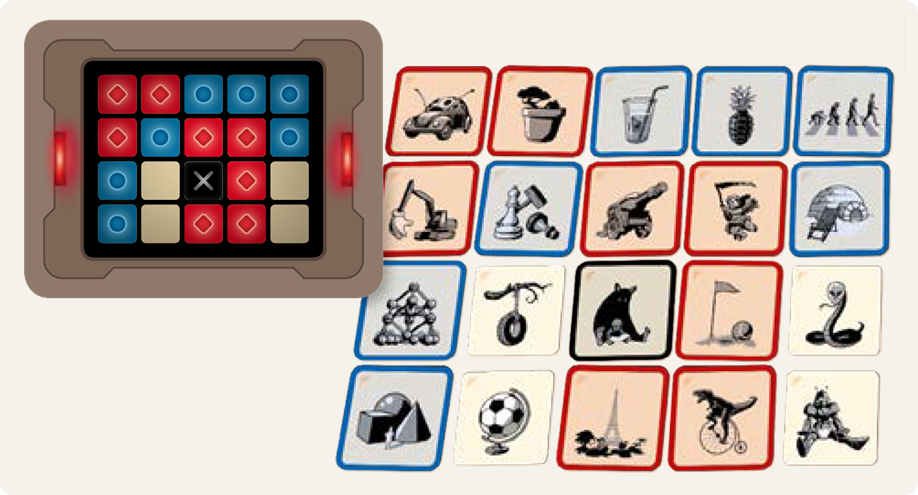
Het spelbord bestaat uit een aantal kaarten die open op tafel gelegd worden in een rechthoekig $$m \times n$$ rooster met $$m$$ rijen en $$n$$ kolommen. Er bestaan twee varianten van het spel: één waarbij er tekeningen op de kaarten staan (zoals in onderstaand $$4 \times 5$$ rooster aan de linkerkant) en één waarbij er woorden op de kaarten staan (zoals in onderstaand $$5 \times 5$$ rooster aan de rechterkant). Daarmee zie je meteen dat het aantal rijen en kolommen van het spelbord kan variëren.

Elk team kiest een speler als hoofd van de geheime dienst. Deze twee spelers nemen plaats aan één kant van de tafel. Hun teamgenoten gaan aan de andere kant van de tafel zitten en zijn geheim agenten die moeten raden waar de spionnen van hun team zich bevinden.

De positie van de spionnen op het spelbord is enkel gekend voor de hoofden van de geheime diensten en staat vermeld op de sleutel van het spel. De sleutel komt overeen met de kaarten van het spelbord en vormt dus zelf ook een $$m \times n$$ rooster met hetzelfde aantal rijen en kolommen als het spelbord. Blauwe vakjes bepalen de plaatjes die het blauwe team moet vinden (blauwe spionnen). Rode vakjes bepalen de plaatjes die het rode team moet vinden (rode spionnen). Witte vakjes zijn onschuldige omstanders en het zwarte vakje is de huurmoordenaar waarmee nooit contact mag gezocht worden.

In een sleutel is er altijd juist één zwart vakje en is het verschil tussen het aantal blauwe en rode vakjes exact gelijk aan één. Het team dat het meeste spionnen moet vinden komt als eerste aan de beurt. In bovenstaande sleutel zijn er bijvoorbeeld 7 blauwe vakjes en 8 rode vakjes, waardoor het rode team als eerste aan de beurt komt.

Een team dat aan de beurt is, kan één van twee mogelijke acties ondernemen: een kaart aanduiden of stoppen. In dat laatste geval komt het andere team aan de beurt. In het eerste geval verklapt het hoofd van de geheime dienst de kleur van het vakje uit de sleutel waarmee de aangeduide kaart overeenkomt (door er een speciale kaart van die kleur op te leggen). De kleur van dat vakje bepaalt welk team als volgende aan de beurt komt: als de kleur van de aangeduide kaart overeenkomt met de kleur van het team dat aan de beurt was, dan blijft het team aan de beurt; anders komt het andere team aan de beurt.

Het spel eindigt als alle spionnen van een team aangeduid zijn of als de huurmoordenaar (zwart vakje) aangeduid wordt. In het eerste geval wint het team waarvan alle spionnen aangeduid werden. In het tweede geval verliest het team dat de huurmoordenaar aangeduid heeft.

Het hoofd van een geheime dienst kan tijdens het spel ook tips geven waarmee zijn team kan achterhalen welke kaarten op het spelbord overeenkomen met de kleur van het team in de sleutel. Hoe het geven van tips precies werkt, is niet relevant voor deze opgave en wordt uitgelegd in de spelregels (tekeningen, woorden).

Opgave

In het rooster van een spelbord en een sleutel worden de rijen van boven naar onder genummerd, en de kolommen van links naar rechts, telkens vanaf nul. Hierdoor kan de positie van een kaart of een vakje voorgesteld worden als een koppel $$(r, k)$$, waarbij $$r$$ (Number) het rijnummer aanduidt en $$k$$ (Number) het kolomnummer.

Een sleutel wordt voorgesteld als een string (String) waarvan de opeenvolgende karakters de kleuren van de vakjes aanduiden: een hoofdletter B voor een blauw vakje, een hoofdletter R voor een rood vakje, een koppelteken (-) voor een wit vakje en een hoofdletter X voor een zwart vakje met de huurmoordenaar. Hierbij worden de vakjes van de sleutel in de leesrichting doorlopen: van links naar rechts en van boven naar onder.

Definieer een klasse Spelbord waarmee het spelbord van een spelletje Codenames kan voorgesteld worden. Bij het aanmaken van een nieuw spelbord (Spelbord) moeten drie argumenten doorgegeven worden: i) het aantal rijen $$m \in \mathbb{N}_0$$ (Number) van het rooster, ii) het aantal kolommen $$n \in \mathbb{N}_0$$ (Number) van het rooster en iii) een sleutel (String). Hierbij mag ervan uitgegaan worden dat er een geldige configuratie van een spelbord en een sleutel doorgegeven worden, zonder dat dit expliciet moet gecontroleerd worden. Initieel is er nog geen enkele kaart op het spelbord aangeduid. Het team dat een extra spion moet vinden, mag beginnen.

Op een spelbord $$s$$ (Spelbord) moet je minstens de volgende methoden kunnen aanroepen:

Een methode toString waaraan geen argumenten moeten doorgegeven worden. De methode moet een stringvoorstelling (String) van spelbord $$s$$ teruggegeven worden, waarvan het formaat kan afgeleid worden uit onderstaand voorbeeld. Daarbij wordt een kaart die nog niet werd aangeduid voorgesteld door een vraagteken (?) en een kaart die wel al werd aangeduid door het karakter van het corresponderende vakje in de voorstelling van de sleutel. De voorstellingen van twee naburige vakjes worden telkens van elkaar gescheiden door één enkele spatie.
Een methode beurt waaraan geen argumenten moeten doorgegeven worden. De methode moet een string (String) teruggeven die aangeeft welk team aan de beurt is: R voor het rode team of B voor het blauwe team.
Een methode stoppen waarmee het team dat aan de beurt is, kan aangeven dat het wil stoppen. Daarmee komt het andere team aan de beurt. Aan de methode moeten geen argumenten doorgegeven worden. De methode moet een verwijzing naar spelbord $$s$$ (Spelbord) teruggeven.
Een methode aanduiden waarmee het team dat aan de beurt is een kaart op spelbord $$s$$ kan aanduiden. Aan de methode moeten het rijnummer $$r$$ (Number) en het kolomnummer $$k$$ (Number) van de aangeduide kaart als afzonderlijke argumenten doorgegeven worden. Hierbij mag de methode ervan uitgaan dat er een geldige positie op spelbord $$s$$ wordt doorgegeven, zonder dat dit expliciet moet gecontroleerd worden. Als de aangeduide kaart eerder al aangeduid werd, dan mag de toestand van spelbord $$s$$ niet wijzigen en wijzigt ook het team dat aan de beurt is niet. De methode moet een verwijzing naar spelbord $$s$$ (Spelbord) teruggeven.
Een methode isAfgelopen waaraan geen argumenten moeten doorgegeven worden. De methode moet een Booleaanse waarde (Boolean) teruggeven die aangeeft of het spel afgelopen is. Dat is het geval van zodra een team al haar spionnen of de huurmoordenaar (zwart vakje) heeft aangeduid.

Als het spel op een spelbord (Spelbord) reeds afgelopen is, dan moet bij het aanroepen van de methoden beurt, stoppen en aanduiden een Error opgeworpen worden met de boodschap spel is afgelopen.

Voorbeeld

        > const codenames = new Spelbord(4, 5, "RRBBBRBRRBB-XR-B-RR-")
> console.log(codenames).toString())
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
> codenames.beurt()
"R"
> codenames.isAfgelopen()
false
> console.log(codenames.aanduiden(2, 3).toString())
? ? ? ? ?
? ? ? ? ?
? ? ? R ?
? ? ? ? ?
> codenames.beurt()
"R"
> codenames.stoppen().beurt()
"B"
> codenames.isAfgelopen()
false
> console.log(codenames.aanduiden(2, 1).toString())
? ? ? ? ?
? ? ? ? ?
? - ? R ?
? ? ? ? ?
> codenames.beurt()
"R"
> console.log(codenames.aanduiden(3, 4).toString())
? ? ? ? ?
? ? ? ? ?
? - ? R ?
? ? ? ? -
> codenames.beurt()
"B"
> console.log(codenames.aanduiden(1, 1).aanduiden(3, 0).aanduiden(0, 2).stoppen().toString())
? ? B ? ?
? B ? ? ?
? - ? R ?
B ? ? ? -
> codenames.beurt()
"R"
> codenames.isAfgelopen()
false
> console.log(codenames.aanduiden(2, 2).toString())
? ? B ? ?
? B ? ? ?
? - X R ?
B ? ? ? -
> codenames.isAfgelopen()
true
> codenames.beurt()
Error: spel is afgelopen
> codenames.stoppen()
Error: spel is afgelopen
> codenames.aanduiden(1, 4)
Error: spel is afgelopen

Opgave

Voorbeeld

Epiloog