Een routeplanner is een puzzel die bestaat uit een kaart in de vorm van een rechthoekig rooster, met aanwijzingen die je helpen om de juiste route te vinden. Aan de randen van het rooster is er een ingang en een uitgang. Een route gaat van de ingang naar de uitgang door zich telkens een weg te banen naar een volgende cel omhoog, omlaag, naar links of naar rechts, maar niet diagonaal. De route mag maar één keer door elke cel passeren.
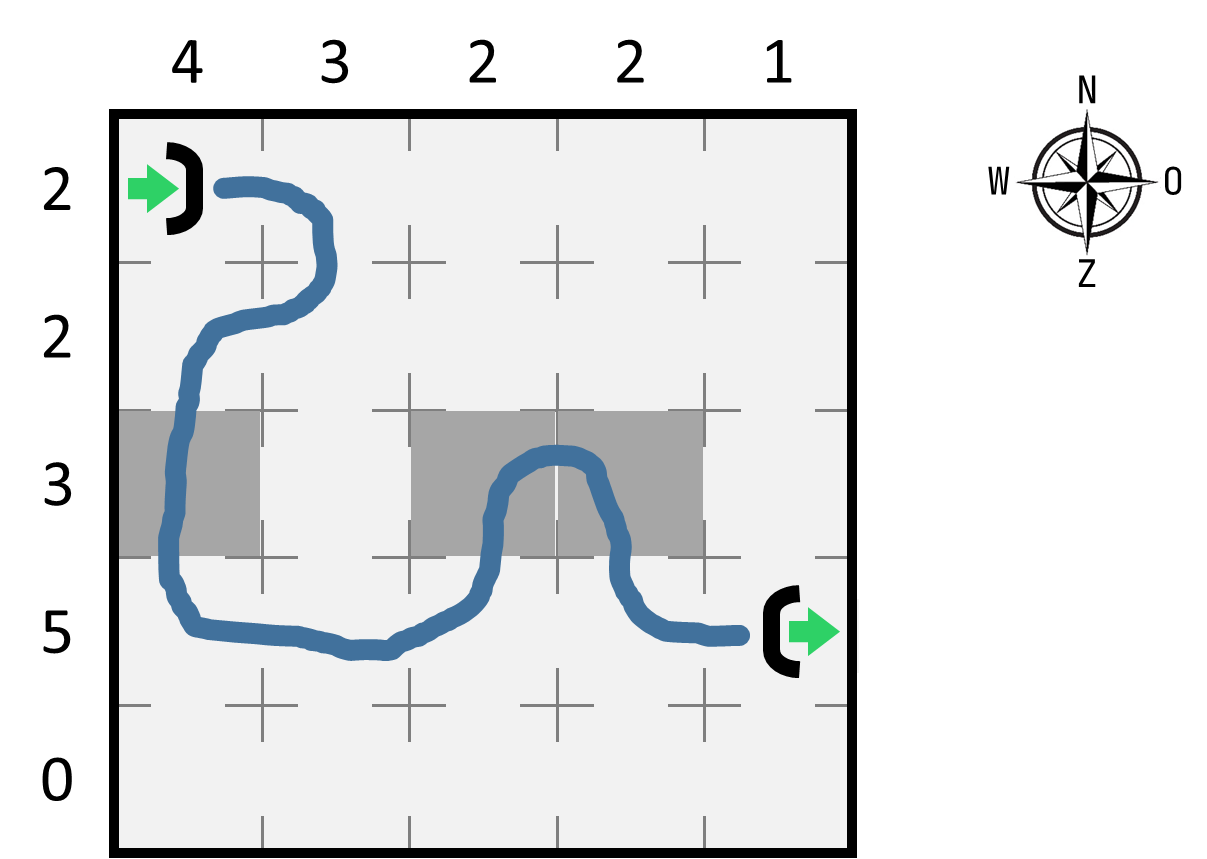
Jouw opdracht is om de route te vinden die de ingang met de uitgang verbindt. Als je dacht dat dit makkelijk is, dan is er nog een bijkomende voorwaarde. Bij elke rij en elke kolom van het rooster staat een getal dat aanduidt hoe vaak de route door de rij of kolom moet passeren. Dit maakt meteen dat er slechts één route is die aan deze voorwaarde voldoet. Het cijfer 3 aan de linkerkant van het bovenstaande rooster geeft bijvoorbeeld aan dat de route door exact drie cellen van de middelste rij moet passeren. We hebben deze cellen in het donkergrijs gearceerd.
Opgave
Het $$m \times n$$ rooster van een routeplanner heeft $$m$$ rijen en $$n$$ kolommen. Om naar de cellen van het rooster te kunnen verwijzen, worden de rijen van boven naar onder genummerd ($$0, 1, \ldots, m - 1$$) en de kolommen van links naar rechts ($$0, 1, \ldots, n - 1$$). Op die manier kan de positie van een cel voorgesteld worden als een reeks (Array) $$(r, k)$$, waarbij $$r$$ (Number) het rijnummer aanduidt en $$k$$ (Number) het kolomnummer.
De vier mogelijke richtingen waarin een route zich kan voortbewegen, worden aangeduid met een hoofdletter (String) die verwijst naar één van de vier hoofdwindrichtingen: N (noord, naar boven), Z (zuid, naar onder), W (west, naar links) en O (oost, naar rechts).
Definieer een klasse Puzzel waarmee routeplanners kunnen voorgesteld en opgelost worden. Bij het aanmaken van een routeplanner (Puzzel) moeten vier argumenten doorgegeven worden: i) een reeks (Array) van $$m$$ natuurlijke getallen (Number) die aangeven hoeveel keer de route door elke rij moet passeren (opgelijst van boven naar onder), ii) een reeks (Array) van $$n$$ natuurlijke getallen (Number) die aangeven hoeveel keer elke route door elke kolom moet passeren (opgelijst van links naar rechts), iii) de positie van de cel met de ingang en iv) de positie met de cel van de uitgang. Hierbij moet gelden dat:
-
de ingang en de uitgang niet aan dezelfde cel liggen
-
de ingang en de uitgang aan een cel op de rand van het rooster liggen
-
het aantal passages van elke rij in het interval $$[0, n]$$ ligt
-
het aantal passages van elke kolom in het interval $$[0, m]$$ ligt
Als minstens één van deze voorwaarden niet voldaan is, dan moet een Error opgeworpen worden met de boodschap ongeldige puzzel. Elke routeplanner (Puzzel) moet een eigenschap positie hebben, die de positie aangeeft van de cel in het rooster waar je je momenteel bevindt. Initieel bevind je je aan de ingang. Voorts moet elke routeplanner (Puzzel) minstens de volgende methoden ondersteunen:
-
Een methode isBinnen waaraan een reeks (Array) met twee getallen $$r$$ en $$k$$ (Number) moet doorgegeven worden. De methode moet een Booleaanse waarde (Boolean) teruggeven, die aangeeft of $$(r, k)$$ de positie aangeeft van een cel binnen het rooster.
-
Een methode isRand waaraan een reeks (Array) met twee getallen $$r$$ en $$k$$ (Number) moet doorgegeven worden. De methode moet een Booleaanse waarde (Boolean) teruggeven, die aangeeft of $$(r, k)$$ de positie aangeeft van een cel op de rand van het rooster.
-
Een methode rijPassages waaraan een getal $$r$$ (Number) moet doorgegeven worden. Als $$r$$ niet in het interval $$[0, m[$$ ligt, dan moet een Error opgeworpen worden met de boodschap ongeldige rij. Anders moet de methode teruggeven door hoeveel cellen (Number) van rij $$r$$ de route reeds gepasseerd is.
-
Een methode kolomPassages waaraan een getal $$k$$ (Number) moet doorgegeven worden. Als $$k$$ niet in het interval $$[0, n[$$ ligt, dan moet een Error opgeworpen worden met de boodschap ongeldige kolom. Anders moet de methode teruggeven door hoeveel cellen (Number) van kolom $$k$$ de route reeds gepasseerd is.
-
Een methode stap waaraan een richting (String) moet doorgegeven worden. De methode moet ervoor zorgen dat je een stap zet in de aangegeven richting. Dit kan ofwel betekenen dat je een stap zet in de tegenovergestelde richting als in de vorige stap (met andere woorden, je keert op je stappen terug) of dat je een stap zet naar een naburige cel waar je nog niet gepasseerd bent. In dat laatste geval moet gelden dat
-
je naar een cel stapt die binnen het rooster ligt
-
je naar een cel stapt waar je nog niet gepasseerd bent
-
je het aantal passages niet overschrijdt van de rij en de kolom waar je naar toe stapt
-
Een methode toString waaraan geen argumenten moeten doorgegeven worden. De methode moet een stringvoorstelling (String) van de routeplanner teruggeven, die is opgemaakt zoals aangegeven in onderstaand voorbeeld. De eerste regel geeft het aantal passages door de kolommen aan. Daarna volgt voor elke rij een regel met het aantal passages door de rij en voor elke cel van de rij (van links naar rechts) een karakter dat de toestand van de cel aangeeft. Daarvoor worden de volgende karakters gebruikt, waarbij geldt dat het karakter gebruikt wordt voor de eerste toestand waaraan de cel voldoet:
-
een asterisk (*): je bevindt je momenteel in deze cel
-
een plusteken (+): de ingang bevindt zich aan deze cel
-
een hekje (#): de uitgang bevindt zich aan deze cel
-
een punt (.): je bent nog niet door deze cel gepasseerd
-
een karakter dat aangeeft via welke twee zijden je de cel bent binnengekomen en terug hebt verlaten: noord-oost (┗), noord-zuid (┃), noord-west (┛), zuid-oost (┏), zuid-west (┓) of oost-west (━)
Tip
Je kunt best deze karakters vanuit de beschrijving naar je code kopiëren, zodat je zeker de juiste karakters gebruikt.
-
Als dat niet het geval is, dan moet een Error opgeworpen worden met de boodschap ongeldige richting. Anders moet de methode de positie teruggeven van de cel waar je naar toe gestapt bent.
Voorbeeld
> const puzzel = new Puzzel([2, 2, 3, 5, 0], [4, 3, 2, 2, 1], [0, 0], [3, 4]);
> puzzel.positie
[0, 0]
> puzzel.isBinnen([2, 3])
true
> puzzel.isBinnen([0, -1])
false
> puzzel.isRand([2, 3])
false
> puzzel.isRand([0, 0])
true
> console.log(puzzel.toString());
43221
2*....
2.....
3.....
5....#
0.....
> puzzel.rijPassages(0)
1
> puzzel.kolomPassages(0)
1
> puzzel.kolomPassages(1)
0
> puzzel.stap("O")
[0, 1]
> puzzel.rijPassages(0)
2
> puzzel.kolomPassages(1)
1
> console.log(puzzel.toString());
43221
2+*...
2.....
3.....
5....#
0.....
> puzzel.stap("N")
Error: ongeldige richting
> puzzel.positie
[0, 1]
> puzzel.rijPassages(1)
0
> puzzel.kolomPassages(1)
1
> puzzel.stap("Z")
[1, 1]
> puzzel.rijPassages(1)
1
> puzzel.kolomPassages(1)
2
> console.log(puzzel.toString());
43221
2+┓...
2.*...
3.....
5....#
0.....
> puzzel.stap("N")
(0, 1)
> console.log(puzzel.toString());
43221
2+*...
2.....
3.....
5....#
0.....
> puzzel.stap("Z")
[1, 1]
> puzzel.stap("W")
[1, 0]
> console.log(puzzel.toString());
43221
2+┓...
2*┛...
3.....
5....#
0.....
> puzzel.stap("W")
Error: ongeldige richting
> puzzel.positie
[1, 0]
> puzzel.stap("Z")
[2, 0]
> puzzel.stap("Z")
[3, 0]
> console.log(puzzel.toString());
43221
2+┓...
2┏┛...
3┃....
5*...#
0.....
> puzzel.stap("Z")
Error: ongeldige richting
> puzzel.positie
[3, 0]
> puzzel.stap("O")
[3, 1]
> puzzel.stap("O")
[3, 2]
> puzzel.stap("N")
[2, 2]
> puzzel.stap("O")
[2, 3]
> puzzel.stap("Z")
[3, 3]
> puzzel.stap("W")
Error: ongeldige richting
> puzzel.positie
[3, 3]
> puzzel.stap("O")
[3, 4]
> console.log(puzzel.toString());
43221
2+┓...
2┏┛...
3┃.┏┓.
5┗━┛┗*
0.....