Victoria amazonica is a species of flowering plant, the largest of the Nymphaeaceae family of water lilies. It thrives at a temperature of 27-30 °C and is native to the shallow waters of the Amazon River basin, such as oxbow lakes and bayous. In Belgium, the plant can be admired in the botanical garden of Ghent University (Ghent) and the National Botanic Garden of Belgium (Meise).
The leaves of V. amazonica are maroon when they reach the surface, but turn green later on. Young leaves have short edges that are curled inwards. Older leaves can grow up to 3 meter in diameter and float on the water's surface on a submerged stalk, 7 to 8 meter in length. The largest leaves can easily carry 40 kg. The underside of the leaves is covered with thorns and prominent ribs that form an irregular pattern of cells.

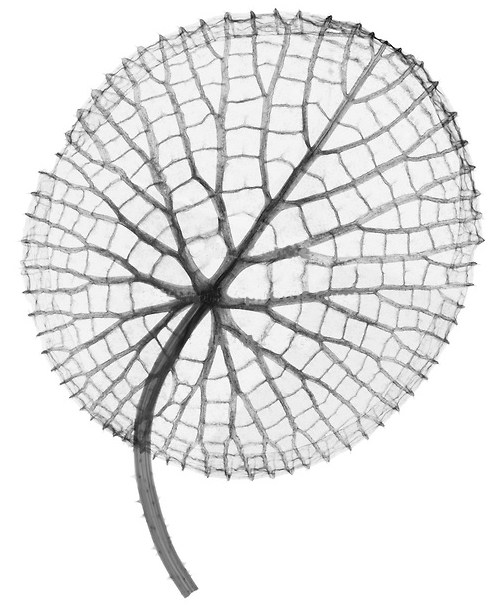
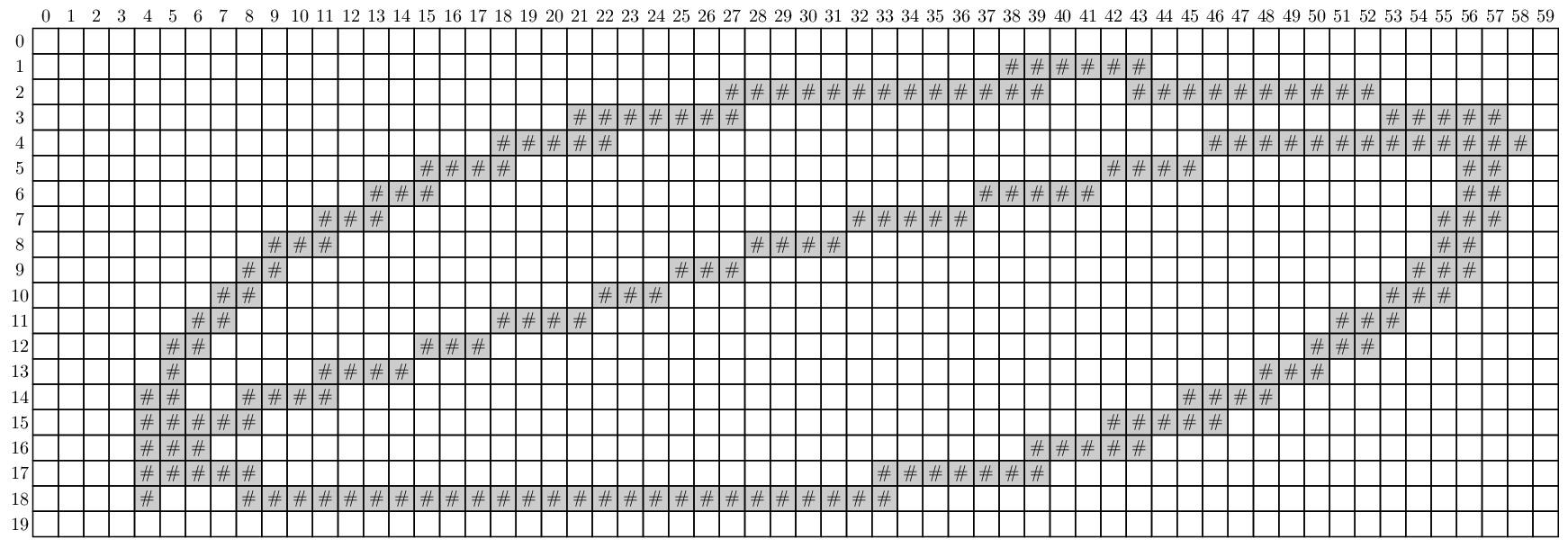
To investigate a plant species we want to count the number of cells on its leaves and determine the average size of these leaf cells. To do this, we convert images of leaves into bitmaps in which leaf cells are clearly delineated. Such a bitmap is nothing more than a rectangular grid and the squares of the bitmap are called bits. Each bit in the grid is either empty (represented by a space) or covered by a piece of rib of the leaf (represented by a pound sign: #). Below you see an example image of a simple leaf having only two cells (left) and the bitmap we have created from this image (right). In a bitmap, leaf cells correspond to regions of contiguous empty bits. Bits are called contiguous if they share a common side. A region of contiguous empty bits is never considered to be a leaf cell, if it contains empty bits on the outer border of the bitmap.

Assignment
Define a class Leaf that can be used to analyze plant leafs. The objects of this class must at least have the following methods:
An initialization method __init__ that takes the location of a text file as an argument. This text file contains a bitmap of the leaf under analysis.
A method __str__ that returns the string representation of the leaf. This string represents the rectangular grid as it is read from the given bitmap file. Apart from empty bits (represented by spaces) and bits that coincide with ribs of the leaf (represented by pound signs: #), bits can also be filled (represented by dots). Filling up bits happens when the fill method is called (see below).
A method fill that takes the row and column index of an empty cell in the bitmap. The rows of a bitmap are indexed top to bottom, the columns left to right, and indexing starts at zero in both cases. If the bit at the given position is not empty, the method must throw an AssertionError with the message bit must be empty. Otherwise, all bits of the region of contiguous empty bits that contains the given empty bit must be marked as filled (they thus are not longer considered empty after the method has been called), and the method must return the number of bits contained in this region.
A method clear that marks all filled bits as empty. Note that the filled bits in the bitmap may belong to multiple leaf cells, for example if the method fill is called multiple times before the method clear is called.
Use the methods fill and clear to write a method cells that returns the number of leaf cells whose size is not smaller than the given minimal cell size. The minimal size of a leaf cell can be passed to the optional parameter minimum (default value: 1). The size of a leaf cell is expressed as the number of bits contained in the corresponding region of contiguous empty bits in the bitmap. Taking into account a minimal cell size is important to exclude small artifacts that might pop up while converting the image of the leaf into its corresponding bitmap. Note again that regions of contiguous empty bits that contain empty bits on the outer border are never considered as leaf cells. These regions must be ignored when the method counts the leaf cells. Make sure that the bitmap has no filled bits after calling this method.
Use the methods fill and clear to write a method cellsize that returns the average cell size of all leaf cells whose size is not smaller than the given minimal cell size. The minimal size of a leaf cell can be passed to the optional parameter minimum (default value: 1). As with the previous method, this method should also not consider regions of contiguous empty bits that contain empty bits on the outer border of the bitmap as leaf cells, and the bitmap may not contain filled bits after the method has been called. The method must return the value None if there are no leaf cells that are larger than or equal to the given minimal cell size.
Example
In the following interactive session we assume that the text files leaf.txt and victoria.txt are located in the current directory. The first file contains the bitmap created from the image of the simple leaf used as an example above. The second file contains a bitmap created from the image of the underside of a leaf of V. amazonica that we have used in the introduction of this assignment.
>>> leaf = Leaf('leaf.txt')
>>> print(leaf)
<BLANKLINE>
######
############# ##########
####### #####
##### #############
#### #### ##
### ##### ##
### ##### ###
### #### ##
## ### ###
## ### ###
## #### ###
## ### ###
# #### ###
## #### ####
##### #####
### #####
##### #######
# ##########################
<BLANKLINE>
>>> leaf.fill(5, 30)
182
>>> print(leaf)
<BLANKLINE>
######
#############...##########
#######.........................#####
#####.......................#############
####.......................#### ##
###.....................##### ##
###..................##### ###
###................#### ##
##...............### ###
##.............### ###
##..........#### ###
##........### ###
#.....#### ###
##..#### ####
##### #####
### #####
##### #######
# ##########################
<BLANKLINE>
>>> leaf.fill(8, 30)
Traceback (most recent call last):
AssertionError: bit must be empty
>>> leaf.fill(15, 30)
335
>>> print(leaf)
<BLANKLINE>
######
#############...##########
#######.........................#####
#####.......................#############
####.......................####..........##
###.....................#####..............##
###..................#####..................###
###................####.......................##
##...............###..........................###
##.............###............................###
##..........####.............................###
##........###................................###
#.....####.................................###
##..####.................................####
#####.................................#####
###................................#####
#####........................#######
# ##########################
<BLANKLINE>
>>> leaf.clear()
>>> print(leaf)
<BLANKLINE>
######
############# ##########
####### #####
##### #############
#### #### ##
### ##### ##
### ##### ###
### #### ##
## ### ###
## ### ###
## #### ###
## ### ###
# #### ###
## #### ####
##### #####
### #####
##### #######
# ##########################
<BLANKLINE>
>>> leaf.cells()
2
>>> leaf.cellsize()
258.5
>>> victoria = Leaf('victoria.txt')
>>> victoria.cells()
242
>>> victoria.cells(minimum=10)
219
>>> victoria.cells(minimum=20)
213
>>> victoria.cellsize()
107.86363636363636
>>> victoria.cellsize(minimum=10)
118.74885844748859
>>> victoria.cellsize(minimum=20)
121.64319248826291