Twins Hansel and Gretel live deep in a forest with their father and stepmother. To prevent that his children would get lost while playing, father has drawn a square grid on a map of the forest, where two consecutive grid lines are always separated 50 meters from each other. Their house is positioned at the location with coordinates $$(0, 0)$$ on the map. Father has marked the trees in the forest that are located at a crossing of two grid lines using a yellow ribbon that contains the $$(x, y)$$ coordinates of the tree, with the $$x$$-coordinate indicating the number of vertical grid lines the tree is positioned to the right of the house, and the $$y$$-coordinate indicating the number of horizontal grid lines the tree is positioned above the house.
When the children leave their house to play in the forest, father only allows them to move to the next tree with a yellow ribbon that is to the right, to the left, above or below their current position, if the sum of the digits of the $$x$$-coordinate and the $$y$$-coordinate on the ribbon is not higher than their age (expressed in years). The tree at position $$(12, 24)$$ can thus only be reached if they are at least $$1 + 2 + 2 + 4 = 9$$ years old. At each tree they visit, they should also leave a breadcrumb in order not to loose their way back home. Hansel and Gretel now have a tradition at each birthday to calculate the number of points in the forest (their house and trees marked by a yellow ribbon) they will be able to reach during the next year. At the age of four, they have marked the following 41 reachable points on a map of the forest.
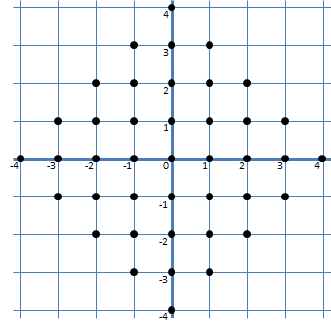
Note that when Hansel and Gretel are 10 years or older, it will no longer be the case that all reachable points around their house form a a square (rotated by 45 degrees). We show some additional figures below, that display the reachable points in white when Hansel and Gretel are $$n$$ years old.

Assignment
The coordinates of a point in the forest are represented as a tuple $$(x, y)$$, with $$x, y \in \mathbb{Z}$$ (int). Your task:
-
Write a function reachable that takes two arguments: i) the coordinates $$(x, y)$$ of a point in the forest and ii) a number $$n \in \mathbb{N}$$ (int). The function must return a Boolean value (bool) that indicates whether the sum of the digits of $$x$$ and $$y$$ is lower than or equal to $$n$$.
-
Write a function neighbors that takes the coordinates $$(x, y)$$ of a point in the forest. The function must return a set containing the coordinates of the four points in the forest that are 50 meters away from the given point.
-
Write a function breadcrumbs that takes an integer $$n \in \mathbb{N}$$ (int) that represents the age (in years) of Hansel and Gretel. The function must return the set containing the coordinates of all points in the forest that Hans and Gretel can reach at the given age.
Algorithm
To determine the coordinates of all points in the forest that Hans and Gretel can reach at the age of $$n$$ years, the following algorithm may be applied. The algorithm uses two sets: a set $$\mathcal{B}$$ holding all reachable points that have been found so far, and a set $$\mathcal{R}$$ of reachable points for which the neighbors still need to be explored:
-
initialization: $$\mathcal{B} = \emptyset,\mathcal{R} = \{(0, 0)\}$$
-
remove a random point $$p$$ from $$\mathcal{R}$$
-
add $$p$$ to $$\mathcal{B}$$
-
add all neighbors of $$p$$ to $$\mathcal{R}$$ that are reachable and are not already in $$\mathcal{B}$$
-
repeat from step 2 until $$\mathcal{R} = \emptyset$$
Here, $$\emptyset$$ represents the empty set.
Example
>>> reachable((0, 0), 0)
True
>>> reachable((10, 20), 3)
True
>>> reachable((2, 3), 4)
False
>>> neighbors((0, 0))
{(0, 1), (0, -1), (1, 0), (-1, 0)}
>>> neighbors((4, 3))
{(4, 2), (4, 4), (3, 3), (5, 3)}
>>> breadcrumbs(0)
{(0, 0)}
>>> breadcrumbs(2)
{(0, 1), (-1, 1), (0, 0), (-1, 0), (0, -2), (0, 2), (2, 0), (-1, -1), (0, -1), (1, 0), (1, -1), (1, 1), (-2, 0)}
>>> len(breadcrumbs(10))
1121
>>> len(breadcrumbs(19))
102485