Besluitvorming over gemiddelde uitkomst
In de sectie 6.4 toonden we dat de parameterschatters van het linear regressie model normaal verdeeld zijn onder de voorwaarden van onafhankelijkheid, lineariteit, homoscedasticiteit en (conditionele) normaliteit van de gegevens. Het regressie model wordt niet enkel gebruikt om de associatie tussen twee variabelen te bestuderen, maar ook om voorspellingen te doen van de response gegeven een gekende waarde voor de predictor. In dat geval wenst men vaak besluitvorming te doen over de gemiddelde uitkomst geschat met het model bij een gegeven waarde \(x\), m.a.w.
\[\hat{g}(x)= \hat{\beta}_0 + \hat{\beta}_1 x\]Hierbij is de gemiddelde uitkomst \(\hat{g}(x)\) een schatter van het conditionele gemiddelde \(E[Y\vert X=x]\). Wanneer de parameterschatters een Normale verdeling volgen zal de schatter voor de gemiddelde uitkomst ook Normaal verdeeld zijn gezien het een lineaire combinatie is van de parameterschatters. Gezien de parameterschatters onvertekend zijn, is de schatter van de gemiddelde uitkomst dat ook.
Men kan aantonen dat de standard error op de schatter voor de gemiddelde uitkomst
\[\text{SE}_{\hat{g}(x)}=\sqrt{MSE\left\{\frac{1}{n}+\frac{(x-\bar X)^2}{\sum\limits_{i=1}^n (X_i-\bar X)^2}\right\}}.\]Dit geeft aan dat de schatter voor de gemiddelde uitkomst het meest precies is voor \(x=\bar x\) en in dit punt zelfs even precies zijn dan wanneer alle observaties \(x_1,\ldots, x_n\) in de steekproef gelijk zouden zijn aan \(x\).
Opnieuw kan men aantonen dat de statistiek
\[T=\frac{\hat{g}(x)-g(x)}{SE_{\hat{g}(x)}}\sim t_{n-2}\]een t-verdeling volgt met \(n-2\) vrijheidsgraden.
Deze statistiek kan opnieuw gebruikt worden voor besluitvorming d.m.v. hypothese testen of door de constructie van betrouwbaarheidsintervallen.
De gemiddelde uitkomst en betrouwbaarheidsintervallen op de gemiddelde uitkomst kunnen eenvoudig worden verkregen in R via de predict(.) functie.
De predictorwaarden (x-waarden) voor het berekenen van gemiddelde uitkomsten kunnen worden meegegeven via het newdata argument.
Betrouwbaarheidsintervallen op de geschatte gemiddelde uitkomsten kunnen worden verkregen d.m.v. het argument interval="confidence".
Zonder het newdata argument wordt de gemiddelde uitkomsten berekend voor alle predictorwaarden van de dataset.
grid <- log2(140:4000)
g <- predict(
lm2,
newdata = data.frame(log2ESR1=grid),
interval = "confidence")
head(g)
## fit lwr upr
## 1 11.89028 10.76082 13.01974
## 2 11.87370 10.74721 13.00019
## 3 11.85724 10.73370 12.98078
## 4 11.84089 10.72028 12.96151
## 5 11.82466 10.70696 12.94237
## 6 11.80854 10.69372 12.92336
De gemiddelde uitkomst en hun 95% puntgewijze betrouwbaarheidsintervallen kunnen eveneens grafisch worden weergegeven (Figuur 33)
brca %>%
ggplot(aes(x = log2ESR1, y = log2S100A8)) +
geom_point() +
geom_smooth(method = "lm") +
xlab("ESR1 (log2)") +
ylab("S100A8 (log2)")
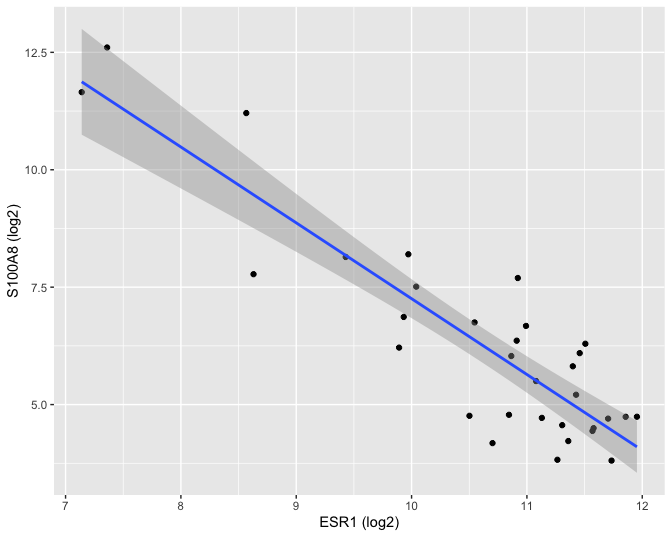
Figuur 33: Scatterplot voor log2-S100A8 expressie in functie van de log2-ESR1 expressie met model schattingen en 95$$\%$$ betrouwbaarheidsintervallen.
De gemiddelde uitkomst en hun 95% betrouwbaarheidsintervallen kunnen makkelijk worden teruggetransformeerd naar de originele schaal, zodat een geometrisch gemiddelde wordt bekomen met 95% betrouwbaarheidsintervallen op het geometrische gemiddelde. Deze kunnen dan grafisch worden weergegeven op de originele schaal in een gewone scatterplot (Figuur 34 links) of in een scatterplot met logaritmische assen (Figuur 34 rechts). In Figuur 34 (links) is het duidelijk dat we met het model na log-transformatie een exponentieel verband kunnen modelleren op de originele schaal.
newdata <- data.frame(cbind(grid= 2^grid, 2^g))
p1 <- brca %>% ggplot(aes(x= ESR1, y = S100A8)) +
geom_point() +
geom_line(aes(x = grid, y = fit), newdata) +
geom_line(aes(x = grid, y = lwr), newdata, color="red") +
geom_line(aes(x = grid, y = upr), newdata, color="red") +
xlab("ESR1") +
ylab("S100A8")
p2 <- brca %>% ggplot(aes(x= ESR1, y = S100A8)) +
geom_point() +
geom_line(aes(x = grid, y = fit), newdata) +
geom_line(aes(x = grid, y = lwr), newdata, color="red") +
geom_line(aes(x = grid,y = upr), newdata, color="red") +
scale_x_continuous(trans = 'log2') +
scale_y_continuous(trans = 'log2') +
xlab("log2 ESR1") +
ylab("log2 S100A8")
gridExtra::grid.arrange(p1, p2, ncol = 2)
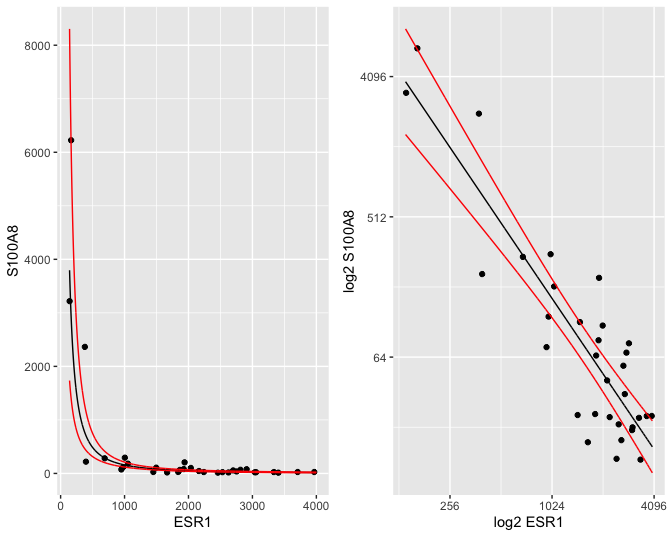
Figuur 34: Scatterplot voor S100A8 expressie in functie van de ESR1 expressie met model schattingen (geometrische gemiddeldes) een 95$$\%$$ betrouwbaarheidsintervallen (links: originele schaal, rechts: originele schaal met logaritmische assen).