De Normale benadering van gegevens

Bij biologische en chemische data is het vaak zo dat het histogram van een continue meting bij verschillende subjecten de karakteristieke vorm heeft van de Normale verdeling. Dat is bijvoorbeeld zo als men een histogram maakt van het logaritme van de totale cholestorol. Rond 1870 opperde de wereldberoemde Belg Adolphe Quetelet (die tevens de eerste student was die een doctoraat behaalde aan de Universiteit Gent) de idee om deze curve als `ideaal histogram’ te gebruiken voor de voorstelling en vergelijking van gegevens. Dit zal handig blijken om meer inzicht te krijgen in de gegevens op basis van een minimum aantal samenvattingsvatten, zoals het gemiddelde en de standaarddeviatie die vaak in wetenschappelijke rapporten vermeld staan.

QQ-plots

Hoewel heel wat metingen in de biologische wetenschappen en scheikunde, zoals concentraties van een bepaalde stof, scheef verdeeld zijn naar rechts, worden ze door het nemen van een logaritme vaak getransformeerd naar gegevens waarvoor het histogram de vorm heeft van een Normale dichtheidsfunctie. Dit is uiteraard niet altijd zo en stappen om te verifiëren of observaties Normaal verdeeld zijn, zijn daarom van groot belang omdat heel wat technieken uit de verdere hoofdstukken er zullen van uit gaan dat de gegevens Normaal verdeeld zijn. Hoewel een vergelijking van het histogram van de gegevens met de vorm van de Normale curve wel inzicht geeft of de gegevens al dan niet Normaal verdeeld zijn, is dit vaak niet makkelijk te zien en wordt de uiteindelijke beslissing nogal makkelijk beïnvloed door de keuze van de klassebreedtes op het histogram. Om die reden zullen we kwantielgrafieken gebruiken die duidelijker toelaten om na te gaan of gegevens Normaal verdeeld zijn.

QQ-plots of kwantielgrafieken (in het Engels: quantile-quantile plots) zijn grafieken die toelaten te verifiëren of een reeks observaties lukrake trekkingen zijn uit een Normale verdeling. Met andere woorden, ze laten toe om na te gaan of een reeks observaties al dan niet de onderstelling tegenspreken dat ze realisaties zijn van een reeks Normaal verdeelde gegevens. Het principe achter deze grafieken is vrij eenvoudig. Verschillende percentielen die men heeft berekend voor de gegeven reeks observaties worden uitgezet t.o.v. de overeenkomstige percentielen die men verwacht op basis van de Normale curve. Als de onderstelling correct is dat de gegevens Normaal verdeeld zijn, dan komen beide percentielen telkens vrij goed met elkaar overeen en verwacht men bijgevolg een reeks puntjes min of meer op een rechte te zien. Systematische afwijkingen van een rechte wijzen op systematische afwijkingen van Normaliteit. Lukrake afwijkingen van een rechte kunnen het gevolg zijn van toevallige biologische variatie en zijn daarom niet indicatief voor afwijkingen van Normaliteit.

Om inzicht te krijgen in QQ-plots simuleren we eerst data uit de normale verdeling om te zien hoe deze plots eruit zien als de data normaal verdeeld zijn.

We simuleren data voor 9 steekproeven met een gemiddeld van 18 en een standaard afwijking van 9.

n <- 20
mu <- 18
sigma <- 9
nSamp <-9

normSim <- matrix(rnorm(n*nSamp,mean=mu,sd=sigma),nrow=n) %>% as.data.frame

We gaan nu de data visualiseren.

Merk op dat de data niet in het tidy formaat is.
De data voor elke groep/simulatie staat naast elkaar in de kolommen.

We converteren het in het tidy formaat via de gather functie. Hierbij wordt een eerste kolom gemaakt samp die de kolomnamen van de originele dataset normSim voor elk overeenkomstig gesimuleerd data punt bij zal houden. De inhoud van de kolommen van de originele dataset normSim, de gesimuleerde waarden, worden opgeslagen in de variable met naam data.
we maken een ggplot histogram voor de variabele data
Aan de hand van de functie facet_wrap kunnen we de data opsplitsen volgens de variabele samp. We krijgen dus een histogram voor elk sample.

normSim %>%
  gather(samp,data) %>%
  ggplot(aes(x=data)) +
  geom_histogram(aes(y=..density.., fill=..count..),bins=30) +
  geom_density(aes(y=..density..)) +
  facet_wrap(~samp)

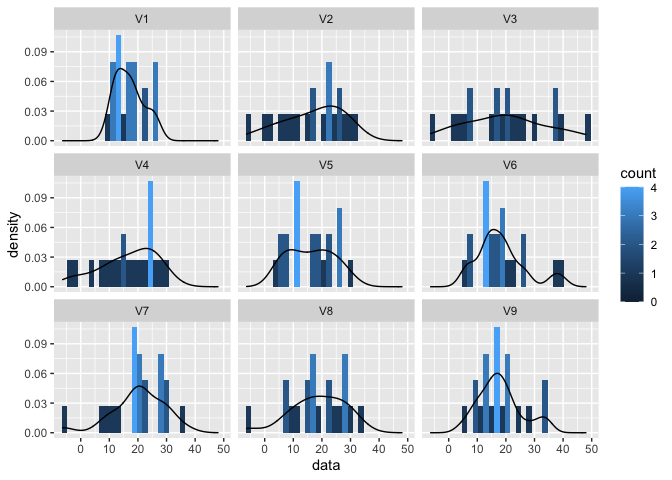
Gezien er vrij weinig data punten zijn en omdat er veel distributies vergeleken moeten worden is het handiger om dit via een boxplot te doen.

normSim %>%
  gather(samp,data) %>%
  ggplot(aes(x = samp,y = data)) +
  geom_boxplot(outlier.shape=NA) +
  geom_point(position="jitter")

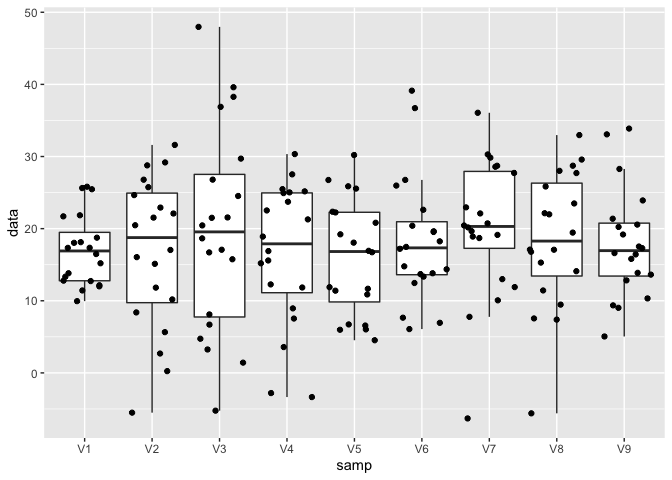
Hoewel alle observaties in alle steekproeven uit dezelfde populatie zijn getrokken zien we toch vrij grote fluctuaties van steekproef tot steekproef in de mediaan, maar zeker ook in de boxgrootte en het bereik van de data in elke steekproef. Dus ondanks het feit dat we over een vrij grote steekproef beschikken (20 observaties) is er toch een grote variabiliteit van steekproef tot steekproef.

We gaan nu normaliteit na via QQ-plot.

Zet data om in tidy data
maak een ggplot object
Voeg een laag toe met de QQ-plot via de functie geom_qq
Voeg een laag toe met de rechte in de QQ-plot via de functie geom_qq_line om te kunnen evalueren hoe goed de data een normale verdeling volgt.

normSim %>%
  gather(samp,data) %>%
  ggplot(aes(sample=data)) +
  geom_qq() +
  geom_qq_line() +
  facet_wrap(~samp)

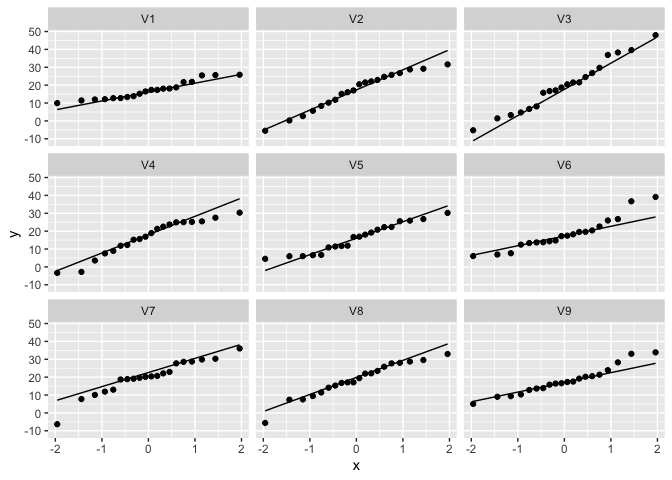
Zelf voor Normal data zien we duidelijk nog afwijkingen door sampling variabiliteit! De plots laten ons toe om ons visueel te trainen om QQ-plots van Normale data te herkennen.

Om de interpretatie van de QQ-plot goed te kunnen illustreren gaan we een histogram en QQ-plot naast elkaar zetten. D.m.v. het package gridExtra kunnen we meerdere GG-plot objecten in een matrix op dezelfde plot afbeelden.

We maken een eerste object aan met het histogram. We slaan dit nu op als object p1 in plaats van dit te visualiseren.
Maak een object p2 met de QQ-plot
Gebruik de functie grid.arrange om de objecten p1 en p2 af te beelden en we geven aan dat we dit in 2 kolommen zullen doen ncol=2. (je kan ook de dimensie in rijen geven (nrow=1))

library(gridExtra)
p1 <- NHANES %>% filter(Gender=="female"&!is.na(BMI)) %>%
  ggplot(aes(x=BMI))+
   geom_histogram(aes(y=..density.., fill=..count..)) +
   xlab("BMI") +
   ggtitle("All females in study") +
  geom_density(aes(y=..density..))

p2 <- NHANES %>% filter(Gender=="female"&!is.na(BMI)) %>%
  ggplot(aes(sample=BMI)) +
  geom_qq() +
  geom_qq_line()

grid.arrange(p1,p2,ncol=2)

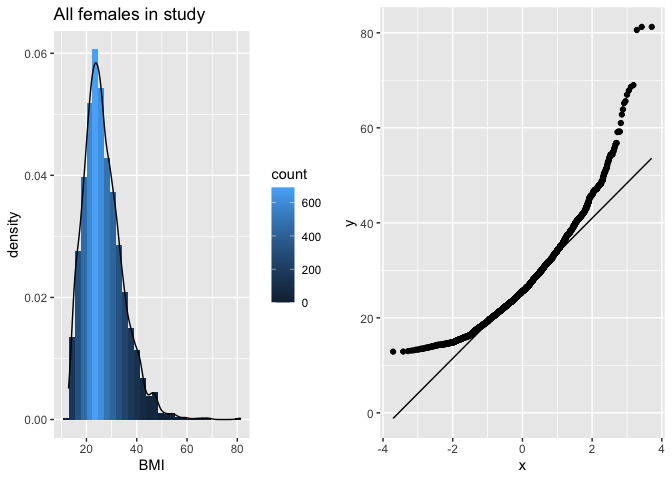
The QQ-plot toont dat de kwantielen van de data in de steekproef

groter zijn (boven de lijn liggen) dan wat we verwachten voor Normaal verdeelde data in de linkerstaart: compressie van de linkerstaart t.o.v. de Normale verdeling. De waarden in de linkerstaart liggen dus dichter bij top van de distributie dan wat we verwachten voor normaal verdeelde data.
groter zijn (boven de lijn liggen) dan wat we verwachten voor Normaal verdeelde data: lange staart naar rechts. De waarden in de rechterstaart liggen dus verder van de top van de distributie dan wat we verwachten voor normaal verdeelde data.

We zien dus duidelijk dat de data scheef verdeeld zijn naar rechts.